机器学习算法总结(六)——EM算法与高斯混合模型

　　极大似然估计是利用已知的样本结果，去反推最有可能（最大概率）导致这样结果的参数值，也就是在给定的观测变量下去估计参数值。然而现实中可能存在这样的问题，除了观测变量之外，还存在着未知的隐变量，因为变量未知，因此无法直接通过最大似然估计直接求参数值。EM算法是一种迭代算法，用于含有隐变量的概率模型的极大似然估计，或者说是极大后验概率估计。

1、经典的三硬币模型　　

　　引入一个例子来说明隐变量存在的问题。假设有3枚硬币，分别记作A，B，C。这些硬币正面出现的概率分别是π，p，q。我们的实验过程如下，先投掷硬币A，根据其结果选出硬币B和硬币C，正面选B，反面选C；然后投掷选出的硬币，此时出现正面记作1，出现反面记作0。在这个例子中我们观察到的变量只是B或者C的结果，而对A的结果并不知道，在这里A的结果也就是我们的隐变量。A的结果对最终的结果是有影响的，因此在估计参数时必须将A的结果考虑进去。

1、EM算法

　　我们将观测变量表示为Y = （Y₁，Y₂，....，Y_n），隐变量表示为Z = （Z1，Z₂，....，Z_n），则观测数据的似然函数可以表示为

　　

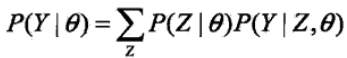
　　在这里P(Y|θ) 是P(Y, Z|θ) 的边缘概率，通过转换后可以表示成右边的形式，我们将其转换成对数形式，这样便于求联合概率

　　

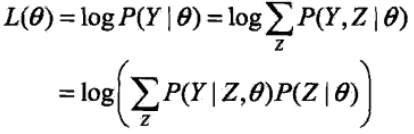
　　然而对于这样的式子直接根据极大化求θ的值是很困难的，因为这里还存在隐变量Z，在这里引入EM算法，通过迭代求解，假设在第i 次迭代后θ的估计值为θ⁽ⁱ⁾。我们希望新估计值能是L(θ)增加，通过迭代逐步的达到最大值。为此我们考虑第i+1步迭代后两者的差：

　　

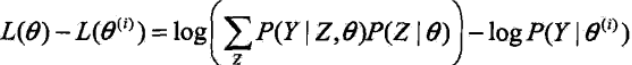
　　利用Jensen不等式将上述式子展开并得到其下界（对数函数是凹函数）：

　　

　　令

　　

　　则有

　　

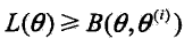
　　在这里B(θ, θ⁽ⁱ⁾) 是L(θ) 的一个下界，而且由的表达式可知

　　

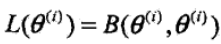
　　因此任何能使得B(θ, θ⁽ⁱ⁾) 增大的θ，也能使得L(θ) 增大。因此求θ值使得B(θ, θ⁽ⁱ⁾) 增大就可以转变成求θ使得L(θ) 增大，即求

　　

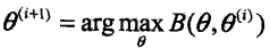
　　将上述式子展开可得（在这里去掉常数项，因为常数项不会影响最终的结果）

　　

　　因此问题就演变成了求Q函数的极大化。EM算法的整体思路就是初始化θ的值为θ⁽⁰⁾，然后通过迭代去求得最终的θ值，迭代的终止条件应该是L(θ) 的增加不明显（具体可以设定一个增加值的阀值来控制）。下面的图可以形象的表示EM算法的迭代更新过程

　　

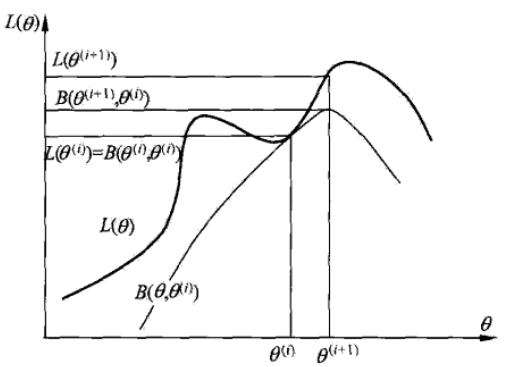
　　EM算法的具体流程如下：

　　输入：观测变量数据Y，隐变量数据Z，联合分布P(Y, Z|θ)，条件分布P(Z|Y, θ)

　　输出：模型参数θ

　　1）选择参数θ的初始值θ(0)，开始迭代

　　2）E步：记θ(i)次迭代参数为θ的估计值，在第i+1次迭代的E步，计算（基于当前求得的模型参数θ猜测隐变量的期望值，因此E步也称为期望步）

　　

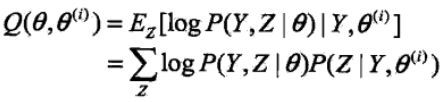
　　3）M步：求使得Q函数极大化的θ值，确定第i+1次迭代的参数的估计值θ(i+1)

　　

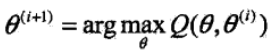
　　4）重复2, 3步直至收敛

　　注意：EM算法是对初始化参数敏感的

2、高斯混合模型（GMM）

　　EM算法的一个重要应用场景就是高斯混合模型的参数估计。高斯混合模型就是由多个高斯模型组合在一起的混合模型（可以理解为多个高斯分布函数的线性组合，理论上高斯混合模型是可以拟合任意类型的分布），例如对于下图中的数据集如果用一个高斯模型来描述的话显然是不合理的

　　

　　对于上图如果我们用两个高斯模型来描述，则如下

　　

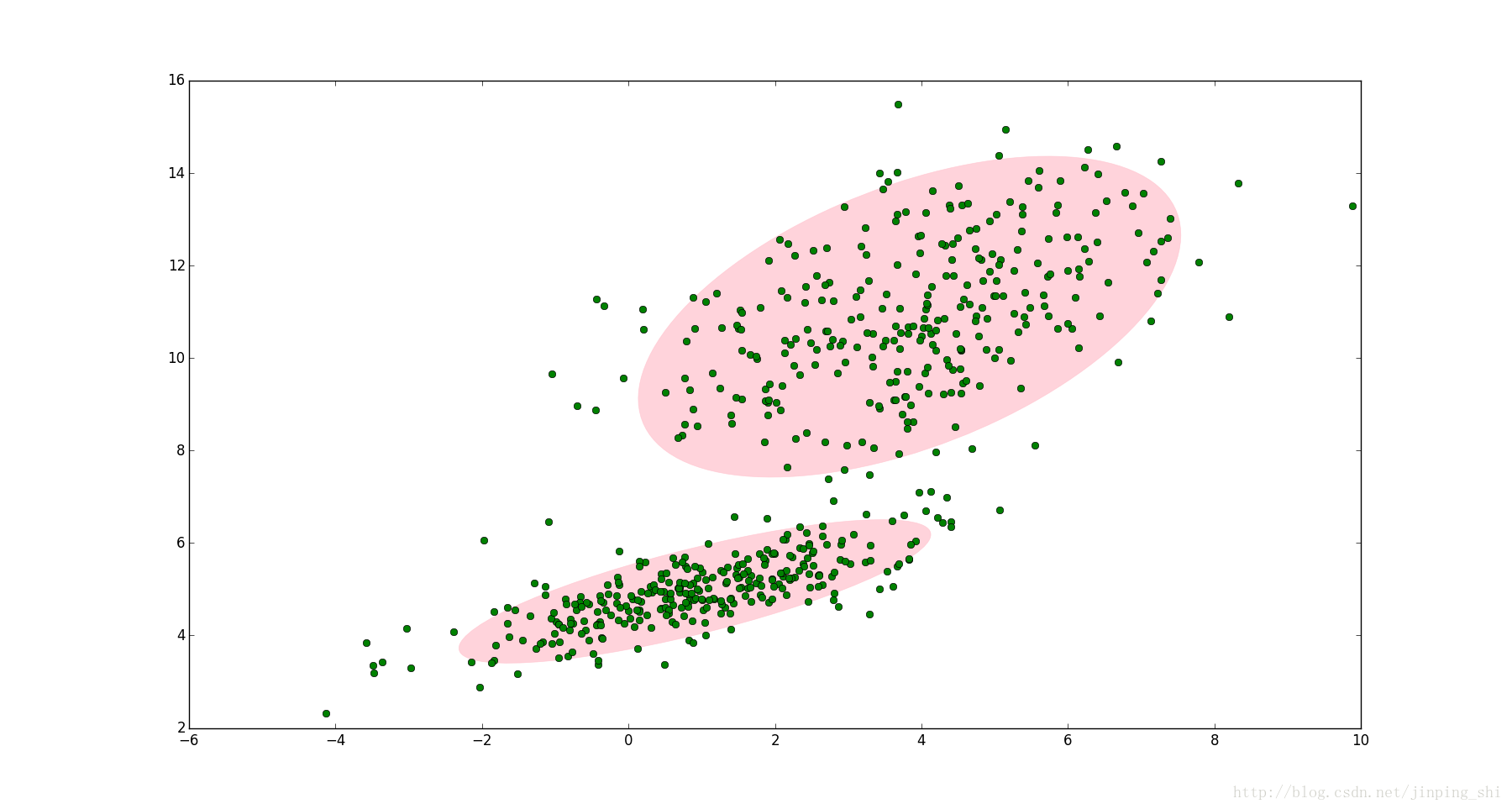
　　然而对于两个高斯模型我们如何将其组合在一起呢，最简单的方式就是通过线性组合的形式来组合，其具体表达式如下：

　　

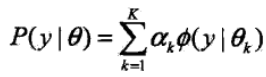
　　其中α_k是系数，α_k ≥ 0，且所有的α总和为1，k表示第k个模型，其中Φ(y|θ_k) 是高斯分布密度（θ_k = （μ_k，σ_k²）），具体表达式如下

　　

　　高斯混合模型常用语聚类中（现实中大多数分布都是正态分布，而在聚类中的各个类别可能是分布参数不同的正态分布）。对于高斯模型的应用大致是先随机在这K个模型中任选一个模型（α_k是第k个模型被选中的概率，注意在这里的混合模型和集成学习中的模型是不一样的，这里实际应用的只是混合模型中的一个），然后再用这个模型进行预测。而且在用高斯混合模型进行聚类时，混合模型中的模型个数k事实上就是聚类的簇数k。

　　用EM算法来估计高斯混合模型的参数，在这里参数θ = (α₁，α₂，...，α_k；θ₁，θ₂，...，θ_k)，在估计之前我们得预先明确隐变量。先假定观测数据y_j（j = 1，2，...，N），具体y_j的产生过程如下，首先依照概率α_k选择第k个高斯分布模型，然后用这个模型生成观测数据y_j。在这里观测数据是已知的，而观测数据具体来自哪个模型是未知的（这就和之前提过的三硬币模型是很相似的，知道模型被选择的概率就好比知道选择B，C硬币的概率，但是却不知道本次预测的结果是由B得出的还是C得出的），因此就引出了我们的隐变量，隐变量的具体表达式如下：

　　

　　γ_jk是0-1随机变量，确定了观测变量和隐变量之后，那么完全数据就是

　　

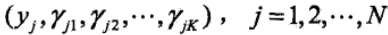
　　之后就可以用EM算法去估计参数θ，具体流程如下

　　1）初始化θ值，开始迭代

　　2）E步：依照当前的模型参数，计算

　　

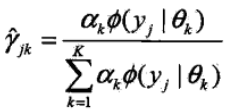
　　3）M步：计算新一轮迭代的模型参数

　　

　　4）重复2, 3步直至算法收敛

　　其实高斯混合模型和K-means（也可以用EM算法描述）方法很相似，简单来说，K-means的结果是每个数据点被分配到其中某一类中，而高斯混合模型是给出这些点被分配给某一类的概率，可以看作是软聚类（也就是允许两个类之间有重合区域）。高斯混合模型是对初始值敏感的，也就是说如果运气不好，选取的初始值不好，最终的模型结果也不会很好，因此很多时候我们会用K-means做预训练，获得较好的结果，然后再用高斯混合模型进行训练进一步优化预测结果（高斯混合模型也是要给出聚类的簇数K值，在初始化参数时给出的）具体的做法就是：先用K-means粗略的估计出簇心，然后将簇心作为高斯混合模型的初始均值（μ值），然后再去估计高斯混合模型中的参数。