洛谷P4774 屠龙勇士

啊我死了。

肝了三天的毒瘤题......他们考场怎么A的啊。

---

大意：

给你若干个形如 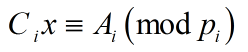的方程组，求最小整数解。

嗯......exCRT的变式。

考虑把前面的系数化掉：

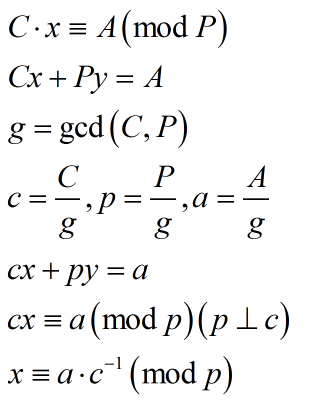
然后就是exCRT板子了。

我TM想要自己写出一个板子，然后GG了......

我快疯了。

然后抄了板子(滑稽)

注意细节，快速幂/乘的时候，b位置不要传负数。

 #include <cstdio>
 #include <set>
 #include <algorithm>

 typedef long long LL;
 const int N = ;

 std::multiset<LL> S;
 std::multiset<LL>::iterator it;
 int n, m, Time, vis[N];
 LL a[N], p[N], awd[N], use[N];

 LL Val;
 LL gcd(LL a, LL b) {
     if(!b) {
         return a;
     }
     return gcd(b, a % b);
 }
 inline LL lcm(LL a, LL b) {
     return a / gcd(a, b) * b;
 }
 void exgcd(LL a, LL b, LL &x, LL &y) {
     if(!b) {
         x = Val / a;
         y = ;
         return;
     }
     exgcd(b, a % b, x, y);
     std::swap(x, y);
     y -= (a / b) * x;
     return;
 }
 inline LL mod(LL a, LL c) {
     while(a >= c) {
         a -= c;
     }
     while(a < ) {
         a += c;
     }
     return a;
 }
 inline LL mul(LL a, LL b, LL c) {
     LL ans = ;
     a %= c;
     b %= c;
     while(b) {
         if(b & ) {
             ans = mod(ans + a, c);
         }
         a = mod(a << , c);
         b = b >> ;
     }
     return ans;
 }
 inline LL qpow(LL a, LL b, LL c) {
     LL ans = ;
     a %= c;
     while(b) {
         if(b & ) {
             ans = mul(ans, a, c);
         }
         a = mul(a, a, c);
         b = b >> ;
     }
     return ans;
 }
 inline LL abs(LL a) {
     return a <  ? -a : a;
 }
 inline LL inv(LL a, LL c) {
     LL x, y;
     Val = ;
     exgcd(a, c, x, y);
     return mod(x, c);
 }
 //----math----

 inline void solve_p1() {
     LL ans = ;
     for(int i = ; i <= n; i++) {
         LL temp = (a[i] - ) / use[i] + ;
         ans = std::max(ans, temp);
     }
     printf("%lld\n", ans);
     return;
 }

 inline void solve_n1() {
     LL g = gcd(use[], p[]);
     if(a[] % g) {
         puts("-1");
         return;
     }
     LL x, y;
     Val = a[];
     exgcd(use[], p[], x, y);
     // use[1] * x + p[1] * y == a[1]
     LL gap = (use[] / g);
     //printf("gap = %lld  y = %lld \n", gap, y);
     LL yy = (y % gap - gap) % gap;
     //printf("yy = %lld \n", yy);
     LL dt = (y - yy) / gap;
     //printf("dt = %lld \n", dt);
     x += dt * (p[] / g);
     //printf("x = %lld \n", x);
     printf("%lld\n", x);
     return;
 }

 inline void solve_a() {
     LL large = ;
     for(int i = ; i <= n; i++) {
         large = std::max(large, (a[i] - ) / use[i] + );
         LL g = gcd(use[i], p[i]);
         if(a[i] % g) {
             puts("-1");
             return;
         }
         if(p[i] == ) {
             vis[i] = Time;
             continue;
         }
         //printf("%lld %lld %lld \n", use[i], p[i], a[i]);
         a[i] /= g;
         p[i] /= g;
         use[i] /= g;
         use[i] %= p[i];
         a[i] %= p[i];
         if(!use[i]) {
             if(!a[i]) {
                 vis[i] = Time;
                 continue;
             }
             else {
                 puts("-1");
                 //printf("%lld %lld %lld \n", use[i], p[i], a[i]);
                 return;
             }
         }
         LL Inv, temp;
         Val = ;
         exgcd(use[i], p[i], Inv, temp);
         Inv = mod(Inv, p[i]);
         //printf("Inv = %lld \n", Inv);
         a[i] = mul(Inv, a[i], p[i]);
     }
     // x = a[i] (mod p[i])

     /*for(int i = 1; i <= n; i++) {
         printf("x === %lld mod %lld \n", a[i], p[i]);
     }*/

     bool fd = ;
     LL A = , P = ;
     for(int i = ; i <= n; i++) {
         //printf("%d \n", i);
         if(vis[i] == Time) {
             continue;
         }
         if(!fd) {
             A = a[i];
             P = p[i];
             fd = ;
             continue;
         }
         // merge i
         LL x, y;
         LL C = ((a[i] - A) % p[i] + p[i]) % p[i];
         LL g = gcd(P, p[i]);
         if(C % g) {
             puts("-1");
             return;
         }
         Val = g;
         exgcd(P, p[i], x, y);
         x = mul(x, C / g, P / g * p[i]);
         A += mul(x, P, P / g * p[i]);
         P *= p[i] / g;
         A = (A + P) % P;
     }
     // x = A (mod P)
     // 1 * x + y * P = A

     LL x, y;
     Val = A;
     exgcd(, P, x, y);
     x = mod(x, P);
     if(x < large) {
         x += P * ((large - x - ) / P + );
     }
     printf("%lld\n", x);
     return;
 }

 inline void solve() {
     scanf("%d%d", &n, &m);
     for(int i = ; i <= n; i++) {
         scanf("%lld", &a[i]);
     }
     for(int i = ; i <= n; i++) {
         scanf("%lld", &p[i]);
     }
     for(int i = ; i <= n; i++) {
         scanf("%lld", &awd[i]);
     }
     for(int i = ; i <= m; i++) {
         LL x;
         scanf("%lld", &x);
         S.insert(x);
     }
     for(int i = ; i <= n; i++) {
         it = S.upper_bound(a[i]);
         if(it != S.begin()) {
             it--;
         }
         use[i] = (*it);
         S.erase(it);
         S.insert(awd[i]);
     }

     //-------------------- p = 1  30pts -------
     bool f = ;
     for(int i = ; i <= n; i++) {
         if(p[i] > ) {
             f = ;
             break;
         }
     }
     if(f) {
         solve_p1();
         return;
     }

     //-------------------- n = 1  30pts -------
     if(n == ) {
         solve_n1();
         return;
     }

     solve_a();
     return;
 }

 int main() {

     int T;
     scanf("%d", &T);
     for(Time = ; Time <= T; Time++) {
         solve();
         if(Time < T) {
             S.clear();
         }
     }

     return ;
 }

AC代码

一共提交了14次.......