数据结构（六）查找---平衡二叉树（ASL）

前提

我们之前的二叉排序树的插入（构建）是按照我们输入的数据来进行的，若是我们的数据分布不同，那么就会构造不同的二叉树

{ , , , , , , , , ,  }

{ , , , , , , , , ,  }

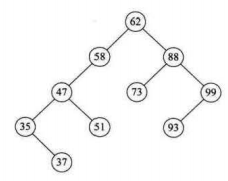
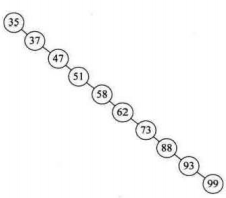
我们发现若是数组元素分布大小按顺序，那么我们极有可能得到一颗极不平衡的二叉树，而二叉树深度越大，查找的次数越多，其查找时间复杂度可以高达O(n),那么如何构造一颗平衡的二叉树？

平衡二叉树

一：定义

平衡：

左右均匀

平衡因子：

将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF(Balance Factor) BF=hl-hr

平衡二叉树（AVL树）：

是一种二叉排序树

空树或任一结点左右子树高度差的绝对值不超过1，即|BF|<=

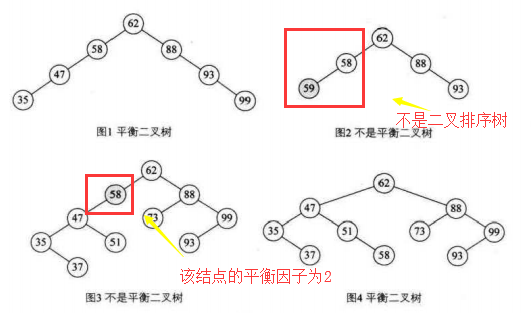
最小不平衡子树

距离插入结点最近的，且平衡因子绝对值大于1的结点为根 的子树，我们称为最小不平衡子树

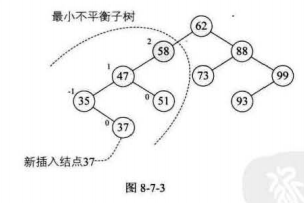
二：平衡二叉树实现原理

基本思想

在构建二叉排序树的过程中，每当插入一个结点时，先检查是否因插入而破坏了树的平衡性，若是，则找出最小不平衡子树。在保存二叉排序树的前提下，调整最小不平衡子树中各个结点之间的链接更新，进行相应的旋转，使之成为新的平衡子树

二叉排序树构建过程

{,,,,,,,,,}

我们若是按照二叉排序树进行构建 图一

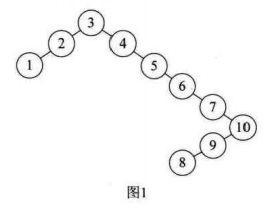
虽然会符合二叉排序树的定义，但是高度达到8的二叉树，查找不好，效率不高，我们应该尽可能是二叉排序树保持平衡，比如图二

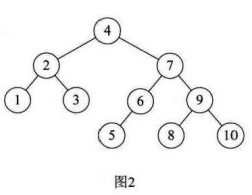
开始构建平衡二叉树AVL

1.选取第一个数据元素3，按照二叉排序树方法正常构建数据，树的平衡因子为0，符合平衡

2.选取第二个数据元素2，按照二叉排序树方法正常构建数据，树的平衡因子为1，符合平衡

3.选取第三个数据元素1，按照二叉排序树方法构建数据位置，树的根节点平衡因子为2，不符合平衡要求，我们找到最小不平衡子树，进行旋转

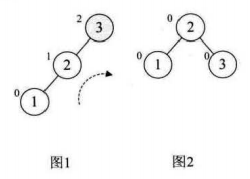
注意：平衡因子为正数，则右转，为负数，则左转

4.选取第四个数据元素4，按照二叉排序树方法正常构建数据，树的平衡因子没改变，符合平衡

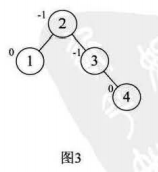
5.选取第五个数据元素5，按照二叉排序树方法正常构建数据，结点3的BF变为-2，说明要进行旋转，我们找到最小不平衡子树，进行旋转

负数，左旋

6.选取第六个数据元素6，按照二叉排序树方法正常构建数据，发现结点2的BF变为-2，说明要进行旋转，而且是左旋

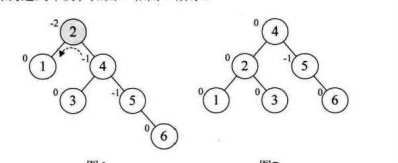
注意：此时本来结点3是结点4的左孩子，由于旋转后，需要满足二叉排序树图像，因此我们将他变为结点2的右孩子

7.选取第七个数据元素7，按照二叉排序树方法正常构建数据，发现结点5的BF变为-2，所以需要对这个最小不平衡子树进行左旋

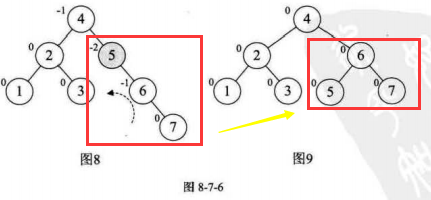
8.选取第八个数据元素10，按照二叉排序树方法正常构建数据，树的平衡因子没改变，符合平衡

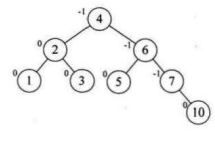
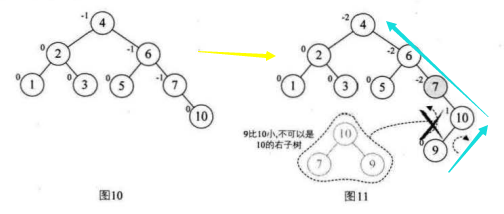
9.选取第八个数据元素9，按照二叉排序树方法正常构建数据，发现结点7的BF值为-2，我们需要进行旋转

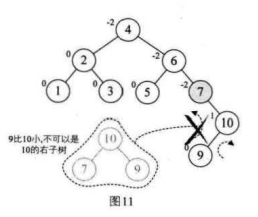
注意：因为我们的结点7的BF=-2，而他的子结点10的BF是1，对于两个符号不统一的最小不平衡子树，
我们都应该先让其符号相同，所以先对我们的最小不平衡子树的子树结点10和结点9安装其结点10的BF=1，正数，先进行两个结点的右旋，

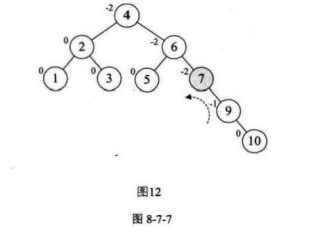
然后再对整个不平衡子树按照结点7的BF=-2进行左旋

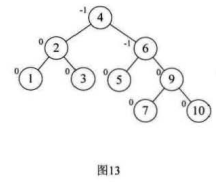
10.选取第九个数据元素8，按照二叉排序树方法正常构建数据，发现结点6的BF=-2，而且最小不平衡子树的符号不统一

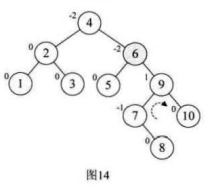
我们先对最小不平衡子树的子树进行旋转，使得其符号统一，按照结点9的BF=，进行右旋

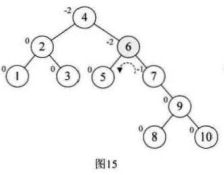
使最小不平衡子树符号相同，然后我们根据结点6的BF=-，进行左旋

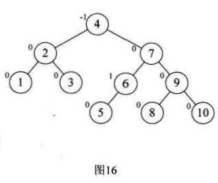
最后将所有的数据排序完成！！！

三：平衡二叉树的难点

1.我们需要知道每个结点的BF值，应该从哪得知？

所以我们要在结构体中加入平衡因子数据域

typedef struct _BiTNode
{
    ElemType data;
    int bf;
    struct _BiTNode* lchild, *rchild;
}BiTNode,*BiTree;

2.我们如何动态修改每个结点的BF值？

（1）我们需要知道，我们插入一个结点，只会影响到该结点到根节点的路径上的结点的BF值，是不会影响到其他结点的BF值

---

---

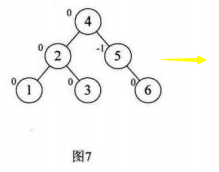
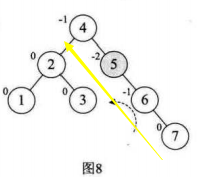
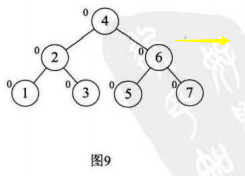
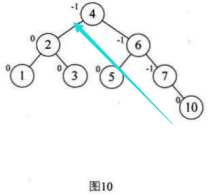
（2）我们插入一个新的结点，那么这个新的结点的BF值一定是0（可以看上图）

（3）我们对一个最小不平衡子树做了平衡处理后，会发现我们只对这个最小不平衡子树的BF进行了改变，而对于这棵树中的其他结点的BF值，虽然变换当中会改变，但是变化后和原来是一样的。

下面我们对添加新结点前，添加后，树平衡调整后的BF值进行观察

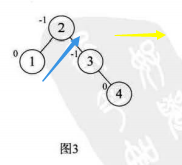
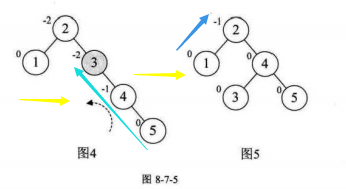
这里不在最小平衡子树中的点有0,1结点，开始和结束后其BF都没有变化

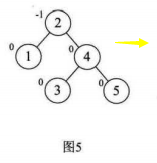
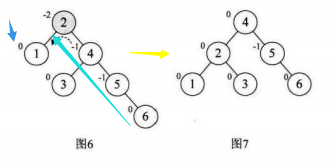
这里不在最小平衡子树中的点有1结点，开始和结束后其BF都没有变化

---

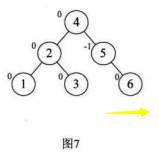
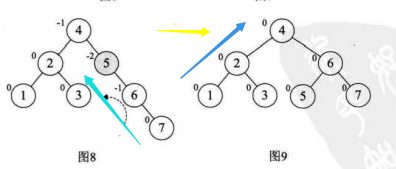
这里不在最小平衡子树中的点有1,,,4结点，开始和结束后其BF都没有变化

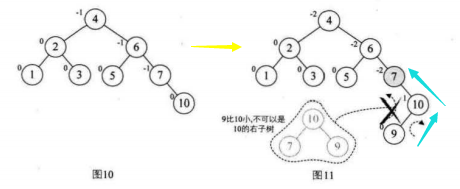
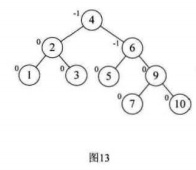
这里不在最小平衡子树中的点有1,,,,,6结点，开始和结束后其BF都没有变化

总之：我们在考虑树的结点的BF值时，我们只需要考虑我们的最小不平衡子树的结点的BF值即可。

（4）同3注意：我们还发现，除了 参与旋转的三个结点，在最小不平衡子树的其他结点的BF值也不会改变

LL型

LR型

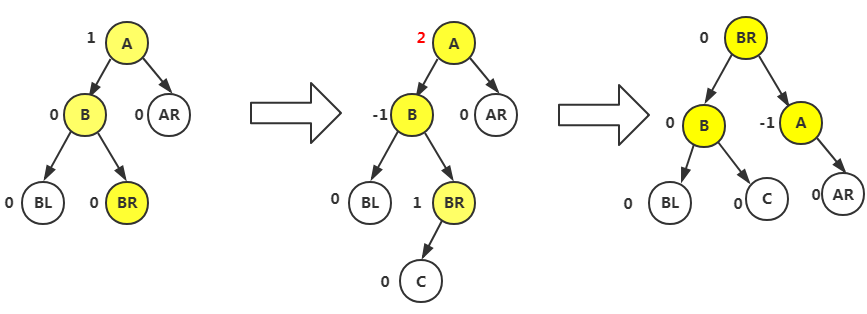
RR和RL型相同

所以：我们只需要考虑的结点是最小不平衡子树的3个旋转结点即可

（5）通过上面分析：我们只需要考虑3个结点的BF值变化即可，但是具体变化方式是不是有规律的？

LL型

插入结点时的变化，我们应该将BL的BF值修改，原来是0，插入子节点后变为1

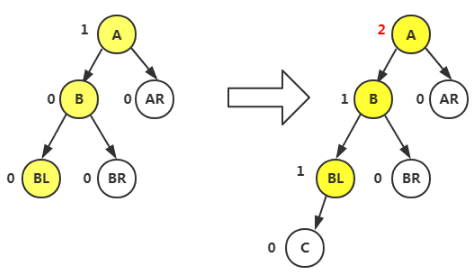
做了平衡旋转后，我们应该将最小不平衡子树的根节点A和左子树根节点B变为0

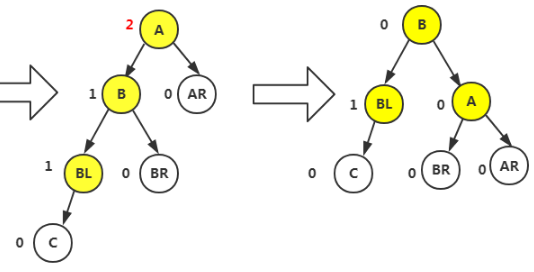
LR型（我们这里只考虑插入在双亲结点左侧：分多种情况，要根据第三个结点再次进行分析）

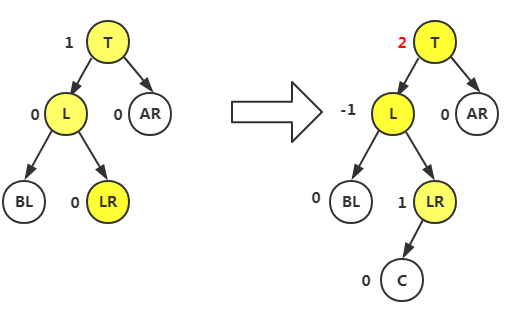
首先是T指向新插入的C结点的双亲BR由原来的0变为1，再向上走T等于其双亲，原来也是0，但是这里是右转所以由0变为-，之后转到A结点，发现是左转，原来BF值是1，直接进入左旋转平衡

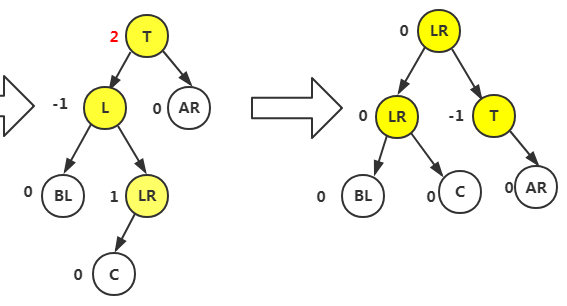
左旋转平衡，根据LR判断，若是为1，我们将最小不平衡子树根T置为-，L和LR结点设为0

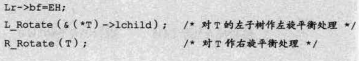
分为这三种情况（想吐）....RR和RL同上面分析。

四：代码实现

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

typedef int Status;
typedef int ElemType;

typedef struct _BiTNode
{
    ElemType data;
    int bf;
    struct _BiTNode* lchild, *rchild;
}BiTNode,*BiTree;

//右旋操作
/*
对以p为根节点的二叉排序树进行右旋操作
处理之后p指向新的树根结点，即旋转处理之前的左子树的根节点
*/
void R_Rotate(BiTree *p)
{
    BiTree L;
    L = (*p)->lchild;
    (*p)->lchild = L->rchild;
    L->rchild = (*p);
    *p = L;
}

//左旋操作
/*
对以p为根节点的二叉排序树进行左旋操作
处理之后p指向新的树根结点，即旋转处理之前的右子树的根节点
*/
void L_Rotate(BiTree *p)
{
    BiTree R;
    R = (*p)->rchild;
    (*p)->rchild = R->lchild;
    R->lchild = (*p);
    *p = R;
}

#define LH +1    //左高
#define EH 0    //等高
#define RH -1    //右高

//左平衡旋转处理代码
//其中传入的T都是最小不平衡子树的根节点
//我们在旋转时主要关注的BF值就是最小不平衡子树的根节点BF和根节点下面的子节点BF值
void LeftBalance(BiTree *T)        //左平衡。我们主要考虑LL,LR两种
{
    BiTree L,Lr;
    L = (*T)->lchild;
    switch (L->bf)    //由于已经是要做平衡处理，所以L->bf不会出现EH状态
    {
    case LH:    //LL直接右旋即可,注意LL后的结点平衡后都是0
        (*T)->bf = L->bf = EH;    //所有的BF跳转都是基于旋转之前的提前调整，方便些
        R_Rotate(T);
        break;
    case RH:    //LR旋转，我们需要注意先要左旋，然后右旋
        //在左右旋之前，我们要修改BF值
        Lr = L->rchild;    //Lr指向T的左孩子的右子树
        switch (Lr->bf)
        { /*  修改T及其左孩子的平衡因子 */
        case LH:
            (*T)->bf = RH;
            L->bf = EH;
            break;
        case EH:
            (*T)->bf = EH;
            L->bf = EH;
            break;
        case RH:
            (*T)->bf = EH;
            L->bf = LH;
            break;
        }
        Lr->bf = EH;
        L_Rotate(&(*T)->lchild);/*  对T的左子树作左旋平衡处理 */
        R_Rotate(T);    /*  对T作右旋平衡处理 */
        break;
    }
}

/*  对以指针T所指结点为根的二叉树作右平衡旋转处理， */
void RightBalance(BiTree* T)
{
    BiTree R, Rl;
    R = (*T)->rchild; /*  R指向T的右子树根结点 */
    switch (R->bf)
    {/*  检查T的右子树的平衡度，并作相应平衡处理 */
    case RH: /*  新结点插入在T的右孩子的右子树上，要作单左旋处理 */
        (*T)->bf = R->bf = EH;
        L_Rotate(T);
        break;
    case LH:/*  新结点插入在T的右孩子的左子树上，要作双旋处理 */
        Rl = R->lchild;/*  Rl指向T的右孩子的左子树根 */
        switch (Rl->bf)
        {
        case RH:
            (*T)->bf = LH;
            R->bf = EH;
            break;
        case EH:
            (*T)->bf = EH;
            R->bf = EH;
            break;
        case LH:
            (*T)->bf = EH;
            R->bf = RH;
            break;
        }
        Rl->bf = EH;
        R_Rotate(&(*T)->rchild);/*  对T的右子树作右旋平衡处理 */
        L_Rotate(T);
        break;
    }
}

/*  若在平衡的二叉排序树T中不存在和e有相同关键字的结点，则插入一个 */
/*  数据元素为e的新结点，并返回1，否则返回0。若因插入而使二叉排序树 */
/*  失去平衡，则作平衡旋转处理，布尔变量taller反映T长高与否。 */
Status InsertAVL(BiTree* T, int e, Status *taller)
{
    if (!*T)
    {
        //插入新结点
        *T = (BiTree)malloc(sizeof(BiTNode));
        (*T)->data = e;
        (*T)->lchild = (*T)->rchild = NULL;
        (*T)->bf = EH;
        *taller = TRUE;
    }
    else
    {
        if (e==(*T)->data)
        {
            //树中已经存在和e有相同的关键字的结点则不再插入
            *taller = FALSE;
            return FALSE;
        }
        else if (e<(*T)->data)
        {
            //应该继续在T的左子树中进行搜索
            if (!InsertAVL(&(*T)->lchild, e, taller))    //未插入
                return FALSE;
            if (*taller)    //已插入到T的左子树中，且左子树长高
            {
                switch ((*T)->bf)    //检测T树的平衡度
                {
                case LH:    //原来是其父节点T的BF值为1，现在插入左孩子，其BF值变为2，直接进行左平衡处理
                    LeftBalance(T);
                    *taller = FALSE;
                    break;
                case EH:    //原来左右子树等高，现因左子树增高而树增高
                    (*T)->bf = LH;
                    *taller = TRUE;
                    break;
                case RH:    //原来右子树比左子树高，现在左右等高
                    (*T)->bf = EH;
                    *taller = FALSE;
                    break;
                }
            }
        }
        else
        {
            //去右子树搜索
            if (!InsertAVL(&(*T)->rchild, e, taller))    //未插入
                return FALSE;
            if (*taller)    //已插入到T的左子树中，且左子树长高
            {
                switch ((*T)->bf)    //检测T树的平衡度
                {
                case LH:    //原来左子树比右子树高，现在左右等高
                    (*T)->bf = EH;
                    *taller = FALSE;
                    break;
                case EH:    //原来左右子树等高，现因右子树增高而树增高
                    (*T)->bf = RH;
                    *taller = TRUE;
                    break;
                case RH:    //原来右子树比左子树高，现在高了两个度，BF=2，需要进行右平衡旋转
                    RightBalance(T);
                    *taller = FALSE;
                    break;
                }
            }
        }
    }
    return TRUE;
}

int main()
{
    int i;
    int a[] = { , , , , , , , , ,  };
    BiTree T = NULL;
    Status taller;
    for (i = ; i < ;i++)
    {
        InsertAVL(&T, a[i], &taller);
    }
    system("pause");
    return ;
}

五：反思

不太熟练，需要多联系，等我把这些都复习一遍，在做题的时候会进行更多的查漏补缺，而且上面缺少删除部分代码，在我真正理解后，会补上