线性插值&双线性插值&三线性插值

http://www.cnblogs.com/yingying0907/archive/2012/11/21/2780092.html

內插是数学领域数值分析中的通过已知的离散数据求未知数据的过程或方法。

根据若干离散的数据，得到一个连续的函数（也就是曲线）或者更加密集的离散方程与已知数据相吻合。这个过程叫做拟合。內插是曲线必须通过已知点的拟合。

1.线性插值

已知坐标 (x0, y0) 与 (x1, y1)，要得到 [x0, x1] 区间内某一位置 x 在直线上的值。

由于 x 值已知，所以可以从公式得到 y 的值

已知 y 求 x 的过程与以上过程相同，只是 x 与 y 要进行交换。

例如，

原来的数值序列：0，10，20，30，40 
线性插值一次为：0，5，10，15，20，25，30，35，40 
即认为其变化（增减）是线形的，可以在坐标图上画出一条直线 。

线性插值经常用于补充表格中的间隔部分。

两值之间的线性插值基本运算在计算机图形学中的应用非常普遍，以至于在计算机图形学领域的行话中人们将它称为lerp。所有当今计算机图形处理器的硬件中都集成了线性插值运算，并且经常用来组成更为复杂的运算：例如，可以通过三步线性插值完成一次双线性插值运算。由于这种运算成本较低，所以对于没有足够数量条目的光滑函数来说，它是实现精确快速查找表的一种非常好的方法。

在一些要求较高的场合，线性插值经常无法满足要求。在这种场合，可以使用多项式插值或者样条插值来代替。

线性插值可以扩展到有两个变量的函数的双线性插值。双线性插值经常作为一种粗略的抗混叠滤波器使用，三线性插值用于三个变量的函数的插值。线性插值的其它扩展形势可以用于三角形与四面体等其它类型的网格运算。

2.双线性插值

在地球物理中，会经常用到双线性插值（Bilinear interpolation）。比如，模拟生成的地表均匀网格上的速度场或者同震位移场。要与GPS观测点上的观测同震位移场进行比较。就必须将均匀网格点的值插值到GPS太站上。这就需要用到双线性插值。

In mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables(e.g, x andy) on a regular grid. The interpolated function should not use the term of x2 or y2, but xy, which is the bilinear form of x and y.

其核心思想是在两个方向分别进行一次线性插值。

The key idea is to perform linear interpolation first in one direction, and then again in the other direction.Although each step is linear in the sampled values and in the position, the interpolation as a whole is not linear but rather quadratic in the sample location (details below).

红色的数据点与待插值得到的绿色点

假如我们想得到未知函数 f 在点 P = (x, y) 的值，假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值。

首先在 x 方向进行线性插值，得到

然后在 y 方向进行线性插值，得到

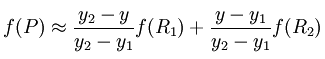
这样就得到所要的结果 f(x, y)，

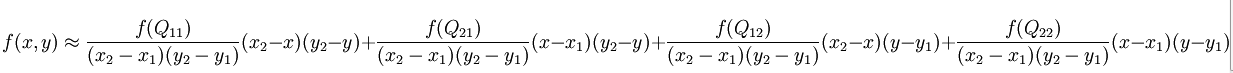
如果选择一个坐标系统使得 f 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简为

或者用矩阵运算表示为

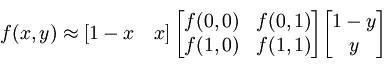
与这种插值方法名称不同的是，这种插值方法并不是线性的，它的形式是

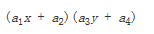
它是两个线性函数的乘积。看到了吧，双线性插值并不是线性。

Contrary to what the name suggests, the bilinear interpolant is not linear

另外，插值也可以表示为

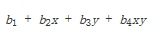
对于单位正方形，

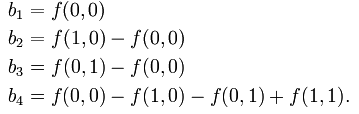
在这两种情况下，常数的数目都对应于给定的 f 的数据点数目。

线性插值的结果与插值的顺序无关。首先进行 y 方向的插值，然后进行 x 方向的插值，所得到的结果是一样的。

双线性插值的一个显然的三维空间延伸是三线性插值。

3.三线性插值

　　三线性插值是在三维离散采样数据的张量积网格上进行线性插值的方法。这个张量积网格可能在每一维度上都有任意不重叠的网格点，但并不是三角化的有限元分析网格。这种方法通过网格上数据点在局部的矩形棱柱上线性地近似计算点 (x,y,z) 的值。

• 三线性插值在一次n=1三维D=3(双线性插值的维数：D=2，线性插值：D=1)的参数空间中进行运算，这样需要(1 + n)^D = 8个与所需插值点相邻的数据点。
• 三线性插值等同于三维张量的一阶B样条插值。
• 三线性插值运算是三个线性插值运算的张量积。

　　实例

　　在一个步距为1的周期性立方网格上，取x_d,y_d,z_d　为待计算点，距离小于　x,y,z,　的最大整数的差值，即，

　　

　　首先沿着z轴插值，得到：

　　

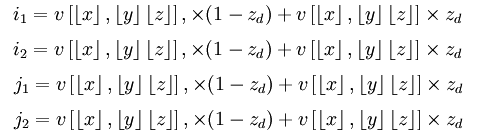
　　然后，沿着y轴插值，得到：

　　w₁ = i₁(1 − y_d) + i₂y_d

　　w₂ = j₁(1 − y_d) + j₂y_d

　　最后，沿着x轴插值，得到：

　　IV = w₁(1 − x_d) + w₂x_d
　　这样就得到该点的预测值。

　　三线性插值的结果与插值计算的顺序没有关系，也就是说，按照另外一种维数顺序进行插值，例如沿着 x、 y、z 顺序插值将会得到同样的结果。这也与张量积的交换律完全一致。