Histogram of Oriented Gridients(HOG) 方向梯度直方图

Histogram of Oriented Gridients，缩写为HOG，是目前计算机视觉、模式识别领域很常用的一种描述图像局部纹理的特征。这个特征名字起的也很直白，就是说先计算图片某一区域中不同方向上梯度的值，然后进行累积，得到直方图，这个直方图呢，就可以代表这块区域了，也就是作为特征，可以输入到分类器里面了。那么，接下来介绍一下HOG的具体原理和计算方法，以及一些引申。

1.分割图像

因为HOG是一个局部特征，因此如果你对一大幅图片直接提取特征，是得不到好的效果的。原理很简单。从信息论角度讲，例如一幅640*480的图像，大概有30万个像素点，也就是说原始数据有30万维特征，如果直接做HOG的话，就算按照360度，分成360个bin，也没有表示这么大一幅图像的能力。从特征工程的角度看，一般来说，只有图像区域比较小的情况，基于统计原理的直方图对于该区域才有表达能力，如果图像区域比较大，那么两个完全不同的图像的HOG特征，也可能很相似。但是如果区域较小，这种可能性就很小。最后，把图像分割成很多区块，然后对每个区块计算HOG特征，这也包含了几何（位置）特性。例如，正面的人脸，左上部分的图像区块提取的HOG特征一般是和眼睛的HOG特征符合的。

接下来说HOG的图像分割策略，一般来说有overlap和non-overlap两种，如下图所示。overlap指的是分割出的区块（patch）互相交叠，有重合的区域。non-overlap指的是区块不交叠，没有重合的区域。这两种策略各有各的好处。

先说overlap，这种分割方式可以防止对一些物体的切割，还是以眼睛为例，如果分割的时候正好把眼睛从中间切割并且分到了两个patch中，提取完HOG特征之后，这会影响接下来的分类效果，但是如果两个patch之间overlap，那么至少在一个patch会有完整的眼睛。overlap的缺点是计算量大，因为重叠区域的像素需要重复计算。

再说non-overlap，缺点就是上面提到的，有时会将一个连续的物体切割开，得到不太“好”的HOG特征，优点是计算量小，尤其是与Pyramid（金字塔）结合时，这个优点更为明显。

2.计算每个区块的方向梯度直方图

将图像分割后，接下来就要计算每个patch的方向梯度直方图。步骤如下：

A.利用任意一种梯度算子，例如：sobel，laplacian等，对该patch进行卷积，计算得到每个像素点处的梯度方向和幅值。具体公式如下：

其中，Ix和Iy代表水平和垂直方向上的梯度值，M(x,y)代表梯度的幅度值，θ(x,y)代表梯度的方向。

B.将360度（2*PI）根据需要分割成若干个bin，例如：分割成12个bin，每个bin包含30度，整个直方图包含12维，即12个bin。然后根据每个像素点的梯度方向，利用双线性内插法将其幅值累加到直方图中。

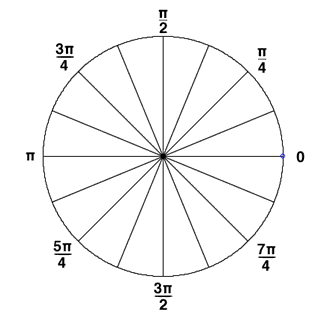
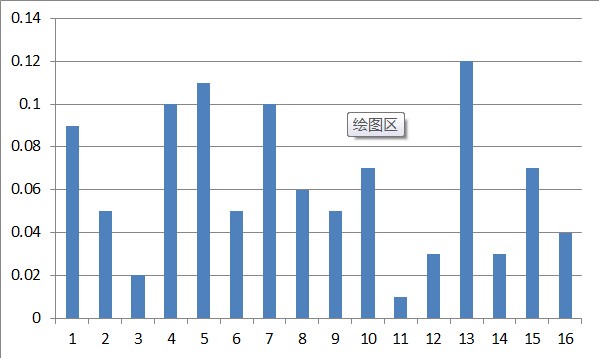
C.（可选）将图像分割成更大的Block，并利用该Block对其中的每个小patch进行颜色、亮度的归一化，这一步主要是用来去掉光照、阴影等影响的，对于光照影响不剧烈的图像，例如很小区域内的字母，数字图像，可以不做这一步。而且论文中也提及了，这一步的对于最终分类准确率的影响也不大。

3.组成特征

将从每个patch中提取出的“小”HOG特征首尾相连，组合成一个大的一维向量，这就是最终的图像特征。可以将这个特征送到分类器中训练了。例如：有4*4=16个patch，每个patch提取12维的小HOG，那么最终特征的长度就是：16*12=192维。

4.一些引申

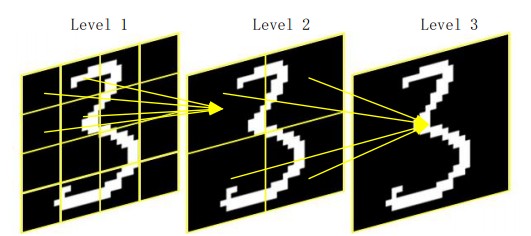
与pyramid相结合，即PHOG。PHOG指的是，对同一幅图像进行不同尺度的分割，然后计算每个尺度中patch的小HOG，最后将他们连接成一个很长的一维向量，作为特征。例如：对一幅512*512的图像先做3*3的分割，再做6*6的分割，最后做12*12的分割。接下来对分割出的patch计算小HOG，假设为12个bin即12维。那么就有9*12+36*12+144*12=2268维。需要注意的是，在将这些不同尺度上获得的小HOG连接起来时，必须先对其做归一化，因为3*3尺度中的HOG任意一维的数值很可能比12*12尺度中任意一维的数值大很多，这是因为patch的大小不同造成的。PHOG相对于传统HOG的优点，是可以检测到不同尺度的特征，表达能力更强。缺点是数据量和计算量都比HOG大了不少。

参考文献：

Navneet Dalal and Bill Triggs，《Histograms of Oriented Gradients for Human Detection》，2005

A. Bosch, A. Zisserman, and X. Munoz, 《Representing shape with a spatial pyramid kernel》，2007