JZOJ 4744.同余

\(\text{Problem}\)

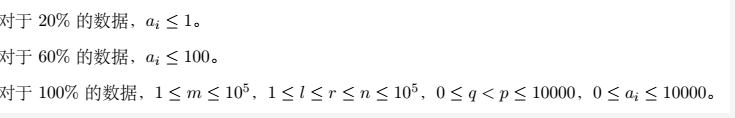
\(\text{Solution}\)

考虑 \(60\) 分

设 \(f_{i,j,k}\) 表示前 \(i\) 个数，模 \(j\) 同余 \(k\) 的个数

由于空间太大，离线后把询问 \(l,r\) 拆开，挂到相应的位置上

然后按位置顺着扫一遍即可

考虑更一般的做法，仍旧离线挂询问

对于 \(p,q\)，需要的 \(a_i\) 一定是 \(px + q\) 形式的

枚举 \(x\) ，记录个数即可

两种做法都无法通过本题

那就平衡规划一番

在 \(p <= 100\) 是采取第一个做法，否则采取第二个做法

\(\text{Code}\)

#include<cstdio>
#include<cmath>
#define re register
using namespace std;

const int N = 1e5 + 5;
int n, m, mx, a[N], ans[N], h[N], buc[N], g[105][105];
struct edge{int nxt, r, fl, p, q, id;}e[N * 2];
inline void add(int r, int fl, int p, int q, int id)
{
	static int tot = 0;
	e[++tot] = edge{h[r], r, fl, p, q, id}, h[r] = tot;
}

inline void read(int &x)
{
	x = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + ch - '0', ch = getchar();
}

int main()
{
	read(n), read(m);
	for(re int i = 1; i <= n; i++) read(a[i]), mx = mx < a[i] ? a[i] : mx;
	int lim = 0;
	for(re int i = 1, l, r, p, q; i <= m; i++)
	{
		read(l), read(r), read(p), read(q), lim = lim < p ? p : lim;
		add(l - 1, -1, p, q, i), add(r, 1, p, q, i);
	}
	lim = sqrt(lim);
	for(re int i = 0; i <= n; i++)
	{
		if (i)
		{
			++buc[a[i]];
			for(re int p = 1; p <= lim; p++) g[p][a[i] % p]++;
		}
		for(re int j = h[i]; j; j = e[j].nxt)
		{
			if (e[j].p > lim)
				for(re int k = 0; k + e[j].q <= mx; k += e[j].p)
					ans[e[j].id] += e[j].fl * buc[k + e[j].q];
			else ans[e[j].id] += e[j].fl * g[e[j].p][e[j].q];
		}
	}
	for(re int i = 1; i <= m; i++) printf("%d\n", ans[i]);
}