《自动控制原理》个人笔记（来自ppt课件）

控制的含义

控制（CONTROL）----某个主体使某个客体按照一定的目的动作。
主体–人：人工控制； 机器：自动控制
客体–指一件物体，一套装置，一个物化过程，一个特定系统。

人工控制与自动控制

人在控制过程中起三个作用：
（1）观测：用眼睛去观测，如温度计、转速表等的指示值；
（2）比较与决策：人脑把观测得到的数据与要求的数据相比较，并进行判断，根据给定的控制规律给出控制量；
（3）执行：根据控制量用手具体调节，如调节阀门开度、改变触点位置。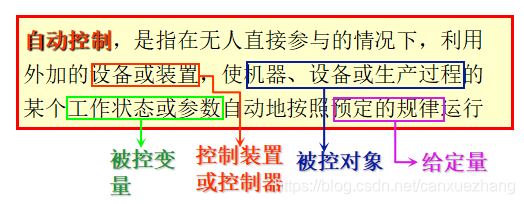

开环控制和闭环控制

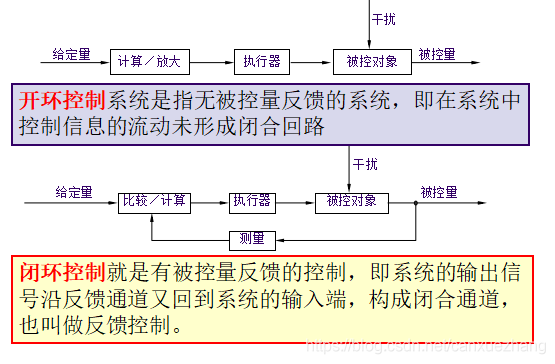
典型开环系统

典型闭环系统

自动控制系统的组成

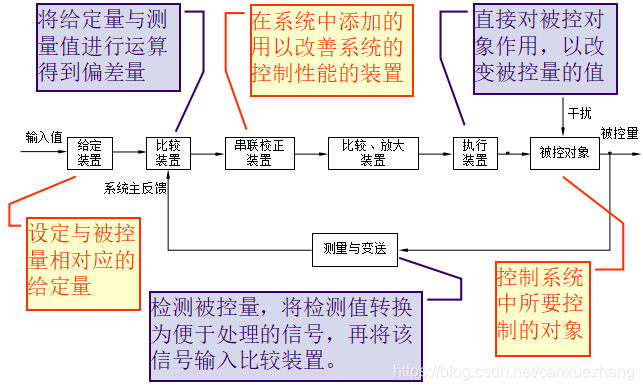
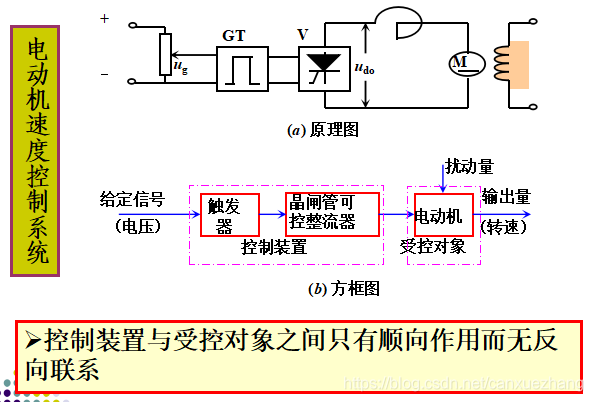
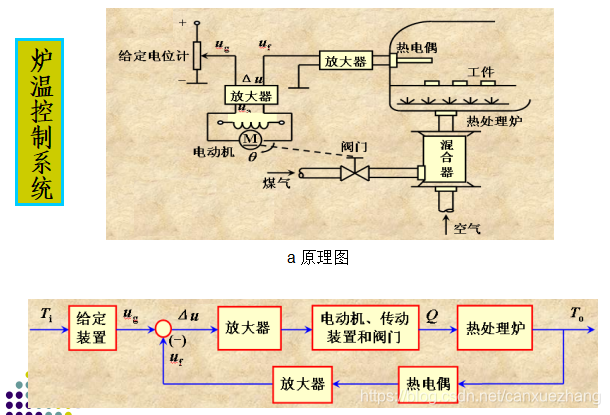
自动控制系统实例

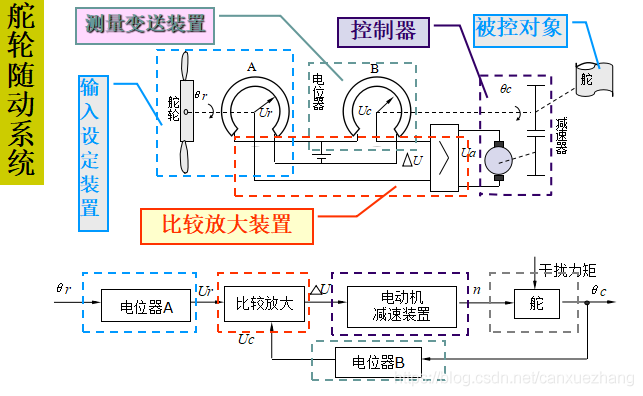
自动控制系统的任务：
被控量和给定值，在任何时候都相等或保持一个固定的比例关系，没有任何偏差，而且不受干扰的影响 。
系统的动态过程：
也称为过渡过程，是指系统受到外加信号(给定值或干扰)作用后，被控量随时间变化的全过程。
自动控制的性能指标：
反映系统控制性能优劣的指标，工程上常常从稳定性、快速性、准确性三个方面来评价。

数学模型基础

控制系统数学模型的概念

描述控制系统输入、输出变量以及内部各变量之间关系的数学表达式，称为系统的数学模型。

建立数学模型的目的

建立系统的数学模型，是分析和设计控制系统的首要工作（或基础工作）。

线性系统的时域数学模型

微分方程

是控制系统最基本的数学模型，要研究系统的运动，必须列写系统的微分方程。

传递函数

控制系统的微分方程是在时间域描述系统动态性能的数学模型，在给定外部作用和初始条件下，求解微分方程可以得到系统的输出响应。这种方法比较直观。
拉普拉斯变换是求解线性微分方程的有力工具，它可以将时域的微分方程转化为复频域中的代数方程，并且可以得到控制系统在复数域中的数学模型——传递函数。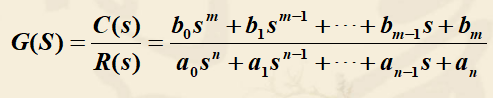

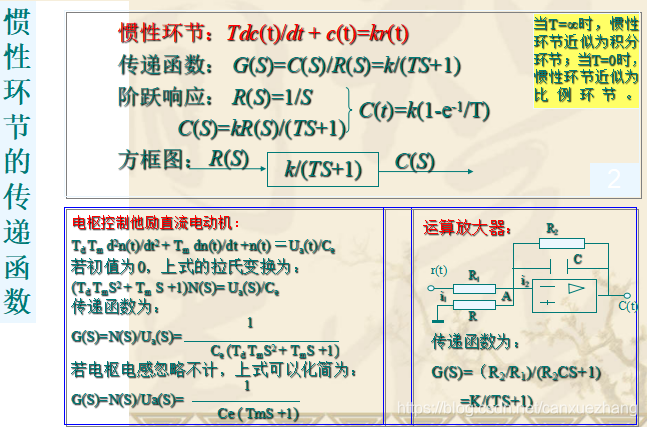
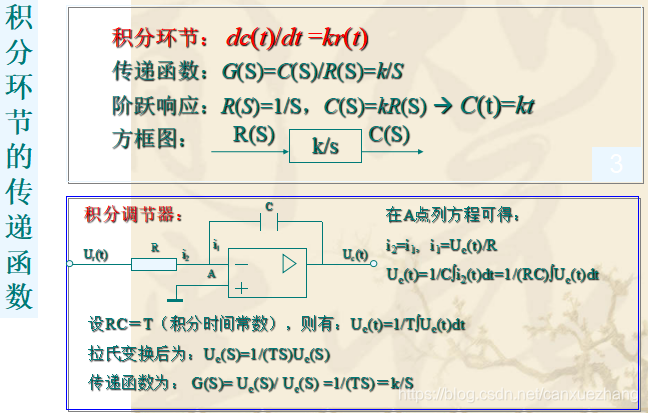
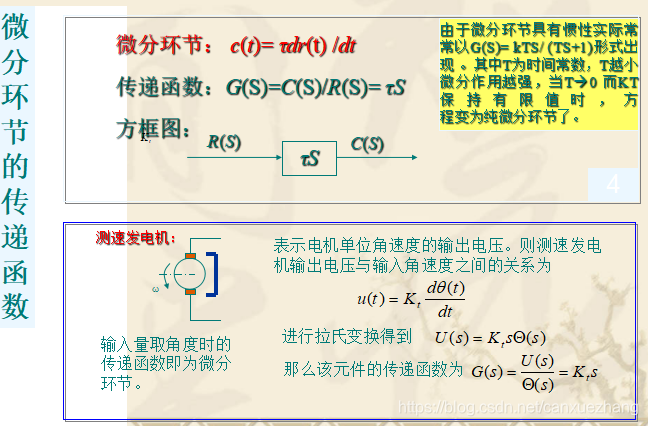
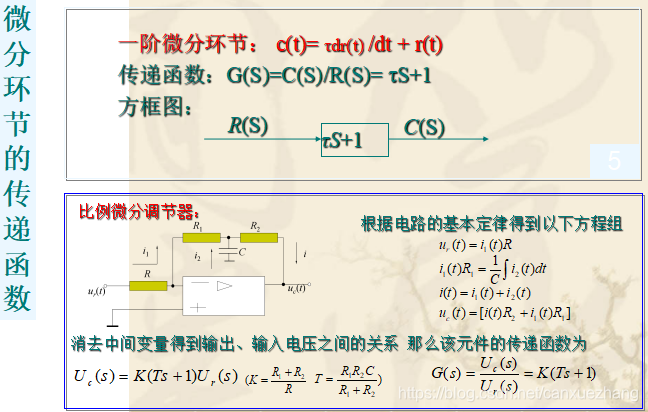
典型环节传递函数

常用的典型环节有比例环节、惯性环节、积分环节、微分环节、振荡环节、延迟环节等。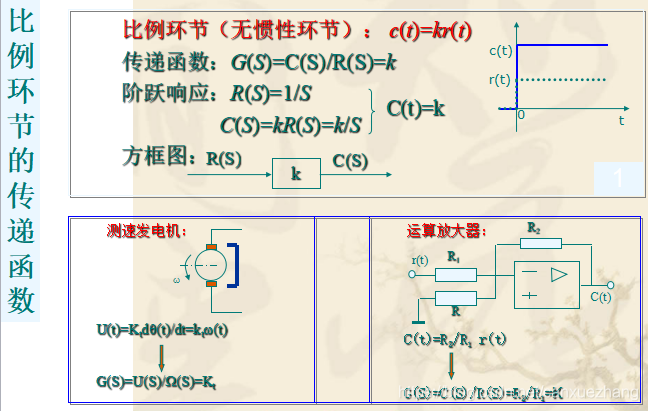

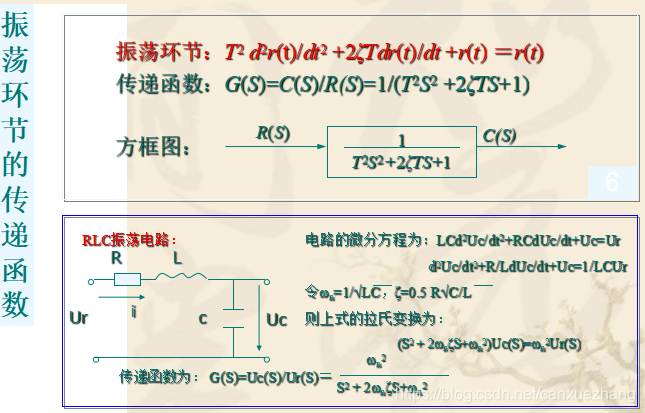
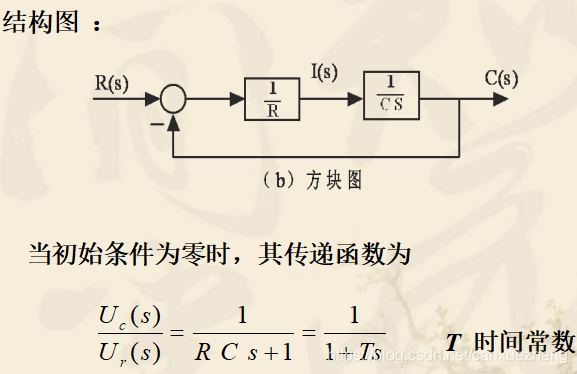
结构图

是数学模型的图解化，它描述了组成系统的各元部件的特性及相互之间信号传递的关系，表达了系统中各变量所进行的运算。

结构图的绘制

绘制系统结构图的根据是系统各环节的动态微分方程式及其拉斯变换。具体步骤如下：

1. 列写系统的微分方程组，并求出其对应的拉斯变换方程组。
2. 从输出量开始写，以系统输出量作为第一个方程左边的量。
3. 每个方程左边只有一个量。从第二个方程开始，每个方程左边的量是前面方程右边的中间变量。列写方程时尽量用已出现过的量。
4. 输入量至少要在一个方程的右边出现；除输入量外，在方程右边出现过的中间变量一定要在某个方程的左边出现。
5. 按照上述整理后拉斯变换方程组的顺序，从输出端开始绘制系统的结构图。

结构图的简化和变换规则

自控系统的典型结构

总之，当求系统的传递函数时，简单的系统可以直接利用结构图求解；复杂的系统可以将其看作信号流图后，利用梅逊公式计算。

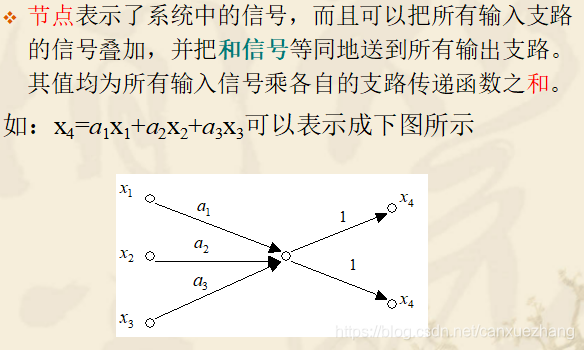
梅逊增益公式

应用梅森公式求解信号流图的具体步骤是

1. 观察信号流图，找出所有的回路，并写出它们的回路增益 L1，L2，L3 ，…… ；
2. 找出所有可能组合的2个，3个，……找出所有可能组合的2个，3个，……
   互不接触（无公共节点）回路，并写出回路增益；
3. 写出信号流图特征式；
4. 观察并写出所有从输入节点到输出节点的前向通道的增益：
5. 分别写出与第k条前向通道不接触部分信号流图的特征式；
6. 代入梅森增益公式。

线性系统的时域分析法

典型输入信号

控制系统的性能评价分为动态性能指标和稳态性能指标两类。为了了解系统的时间响应，必须了解输入信号的解析表达式。

线性定常系统的时域响应

稳态性能指标

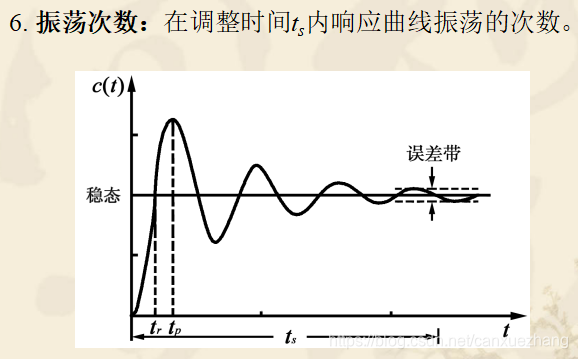
动态性能指标

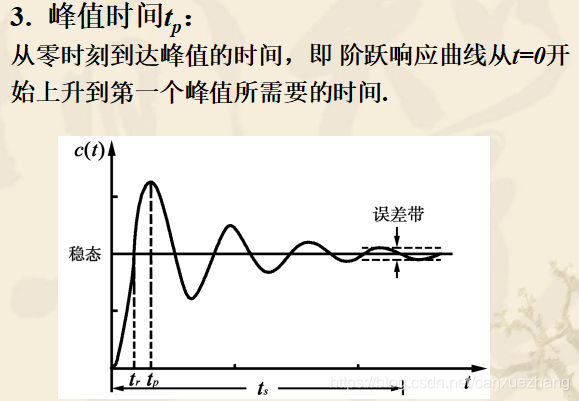
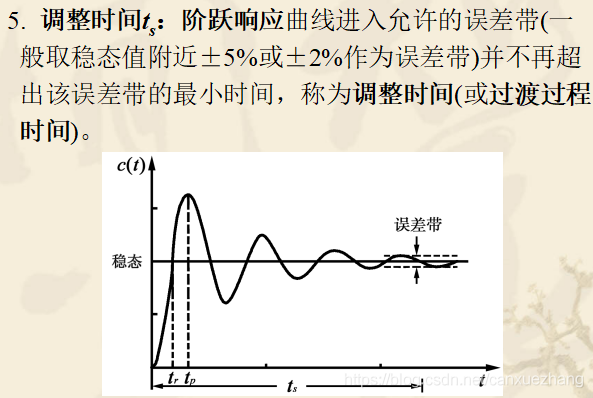
一阶系统的时域分析

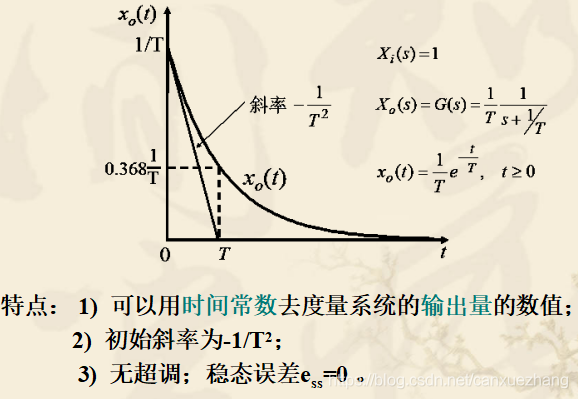
一阶系统的单位阶跃响应

一阶系统的单位脉冲响应

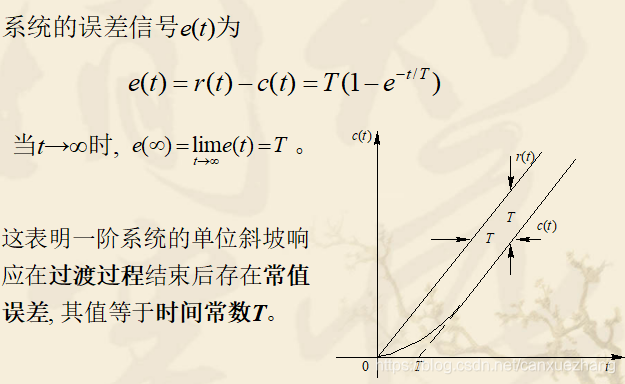
一阶系统的单位斜坡响应

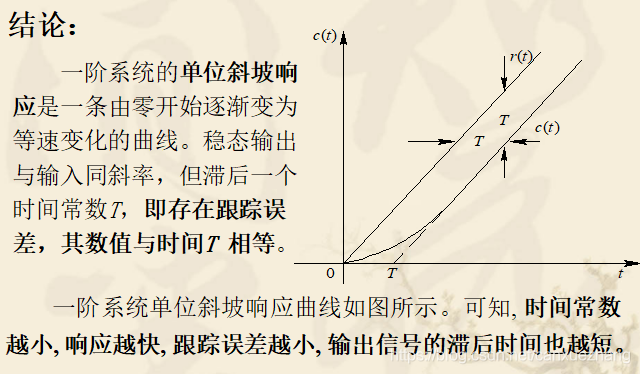
二阶系统的时域分析

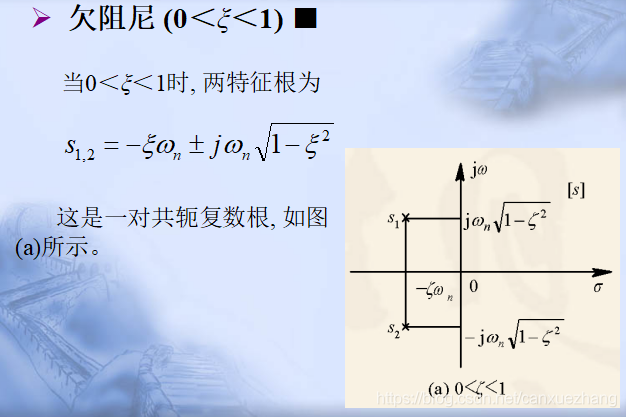
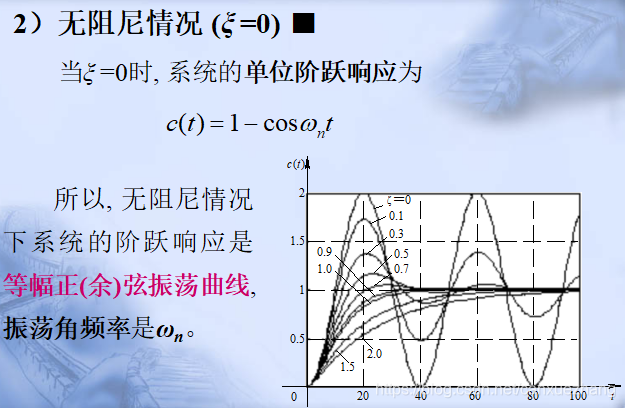
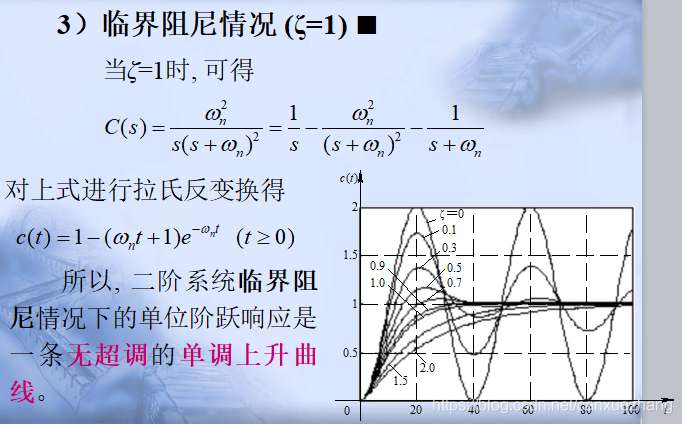
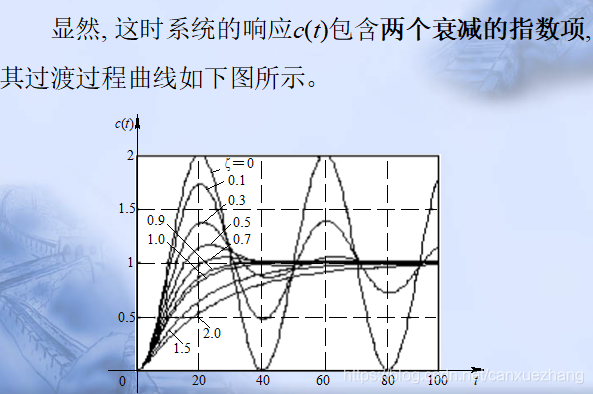
二阶系统的单位阶跃响应

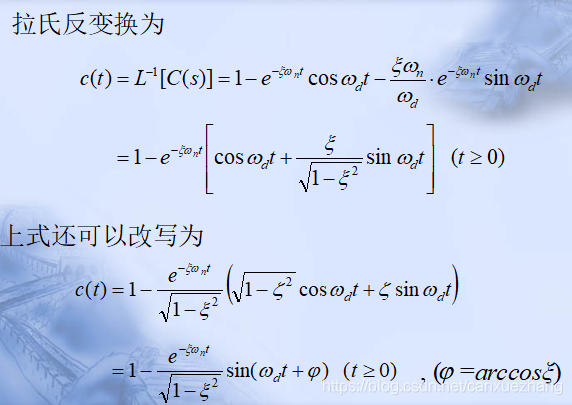
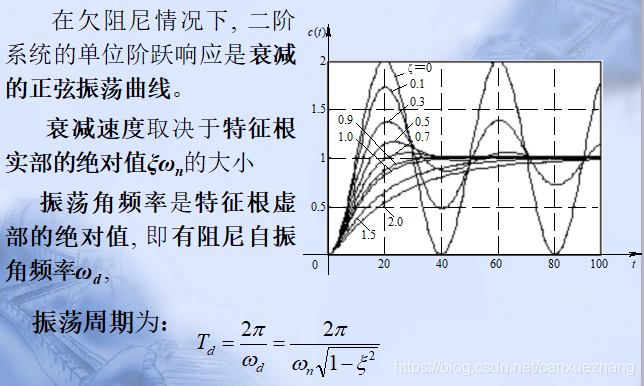
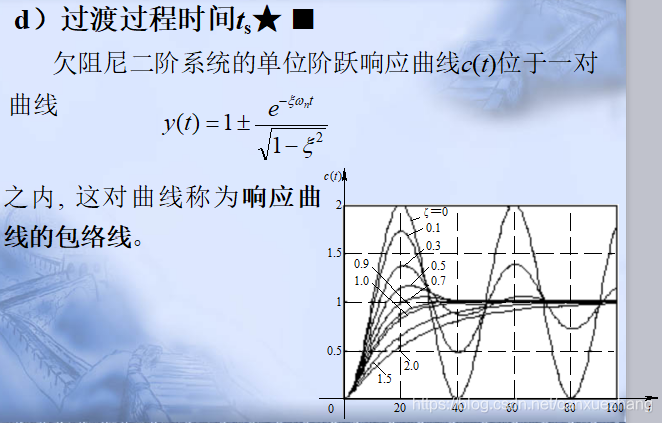
二阶系统的性能指标

线性系统的稳定性分析

劳斯稳定判据

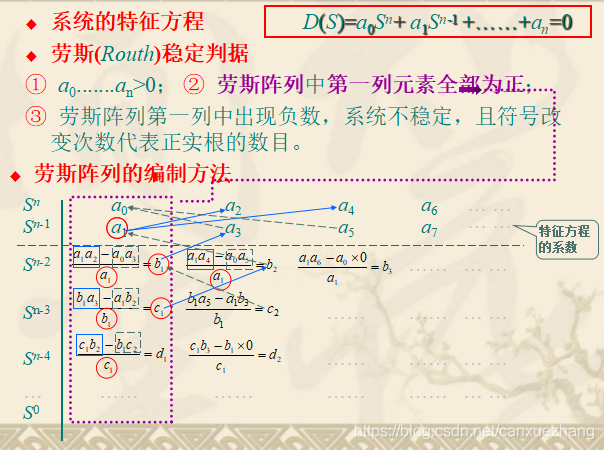
系统参数对稳定性的影响

应用代数判据不仅可以判断系统的稳定性，还可以用来分析系统参数对系统稳定性的影响。

控制系统的稳态误差

误差与稳态误差

根据控制系统的一般结构, 可以定义系统的误差与稳态误差。

控制系统的一般结构

系统的类型

稳态误差的计算

设定输入作用下系统稳态误差的计算

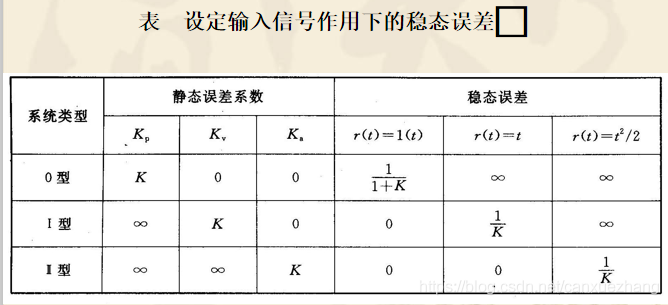
扰动输入作用下系统稳态误差的计算

1.  
   对于扰动输入作用下系统稳态误差的计算, 也可以按照类似设定输入情况的方法进行计算。
2.  
   在这种情况下, 稳定误差的计算稍复杂些, 这里就不再加以论述。
3.  
    

• 1
• 2

第四章 根轨迹法

什么是根轨迹？

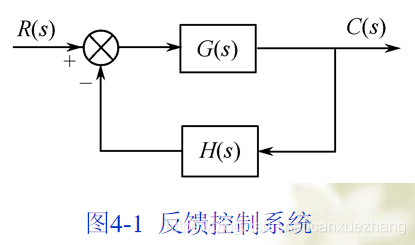
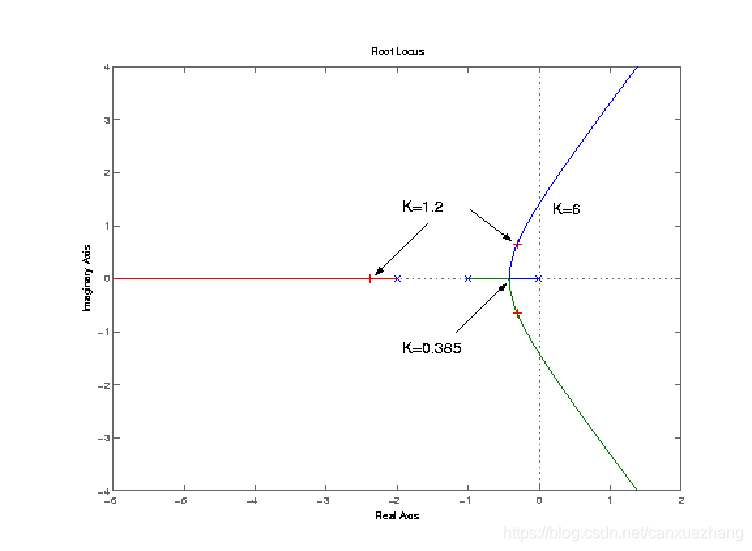
图4-2 根轨迹图
从根轨迹图可以看到：当0<K<0.385时三个闭环极点都是负实数;
当K>0.385时有两个闭环极点成为共轭复数，只要0<K<6闭环系统一定稳定。
一但K值给定，比如K=1.2，3个闭环极点就是3支根轨迹上3个特定点（标有+号的点）。
可见，根轨迹清晰地描绘了闭环极点与开环增益K的关系。

相角条件

今天，在计算机上绘制根轨迹已经是很容易的事，由于计算机强大的计算能力，所以计算机绘制根轨迹大多采用直接求解特征方程的方法，也就是每改变一次增益K求解一次特征方程。
让K从零开始等间隔增大，只要K的取值足够多足够密，相应解特征方程的根就在S平面上绘出根轨迹。
传统的根轨迹法是不直接求解特征方程的，它创造了一套行之有效的办法——图解加计算的手工绘图法。

绘制典型根轨迹

我们可以把现有的绘制根轨迹图的方法分为三类：

1）手工画概略图（草图）

1.  
   这种方法适合调试现场的应急分析、项目开始的粗略分析等不要求很精确的场合。
2.  
   一个熟习根轨迹基本规则的人几分钟就可以画出一张很有用的概略图。

• 1
• 2

2）手工图解加计算画准确图

   这种方法曾经沿用很久，以往的教科书讲述了很多绘图的技艺，不仅繁琐，精度也差，这类方法在实际应用中已逐步淘汰。

• 1

3）计算机绘制精确图

   目前主要指用Matlab工具绘制根轨迹图。它准确快捷，短时间内可以对多个可调参数进行研究，有效地指导设计与调试。

• 1

开环零极点与相角条件

图4-3 相角条件的图示

基本规则

纯粹用试验点的办法手工作图，工作量是十分巨大的，而且对全貌的把握也很困难，于是人们研究根轨迹图的基本规则，以便使根轨迹绘图更快更准。

概括起来， 以开环增益K为参变量的根轨迹图主要有下列基本规则：

控制系统的频域分析

频 率 特 性

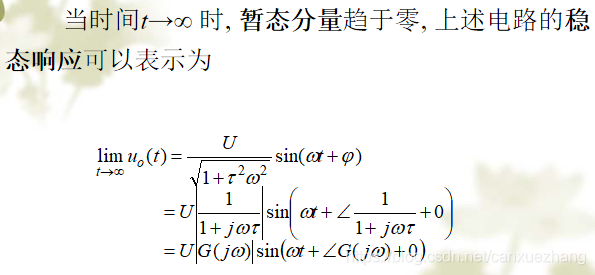
频率特性的求取

频率特性及其表示法

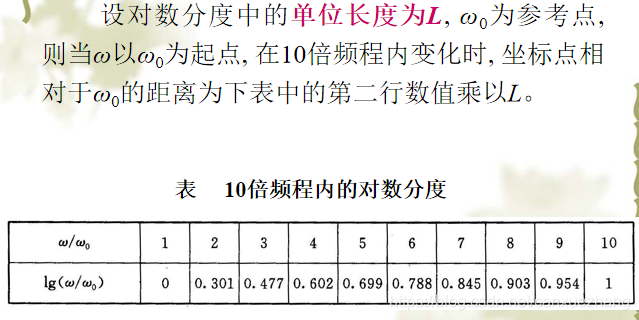
伯德图

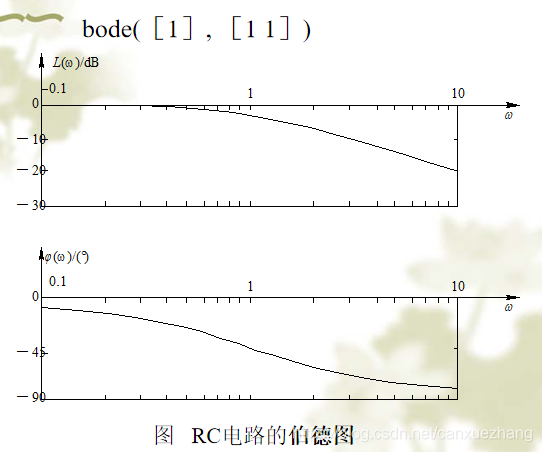
典型环节的频率特性

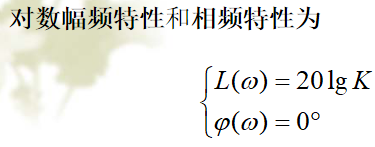
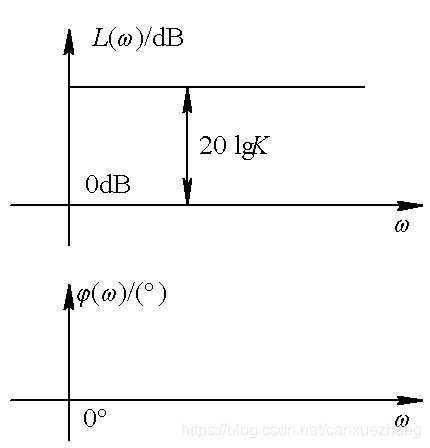
图 比例环节的伯德图


图 积分环节的伯德图


图 微分环节的伯德图







图 惯性环节的Bode图



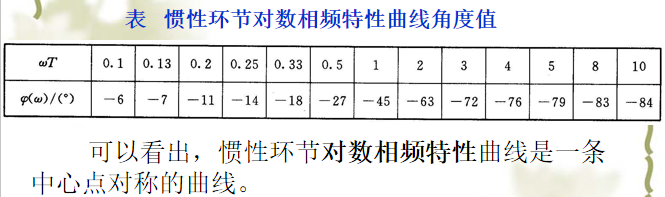
图 MATLAB绘制的惯性环节的伯德图


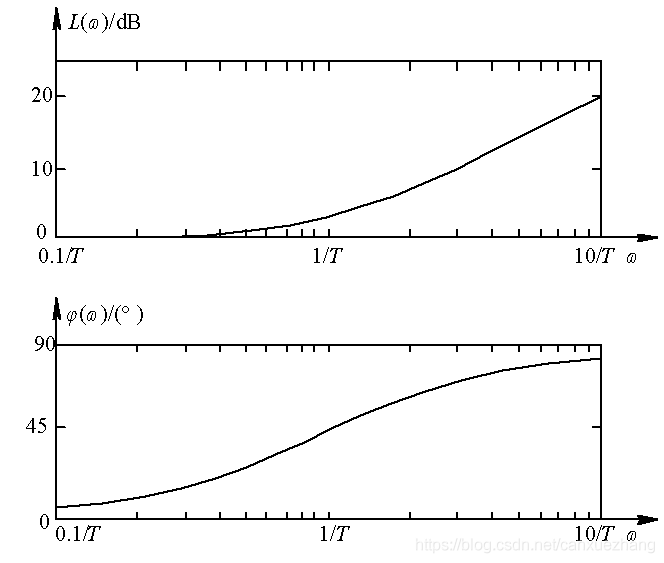
图 一阶微分环节的伯德图





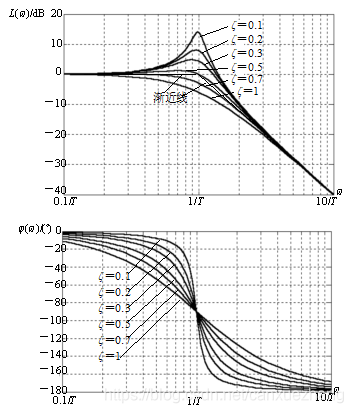
图 二阶振荡环节的伯德图

表 二阶振荡环节对数幅频特性曲线渐近线和精确曲线的误差(dB)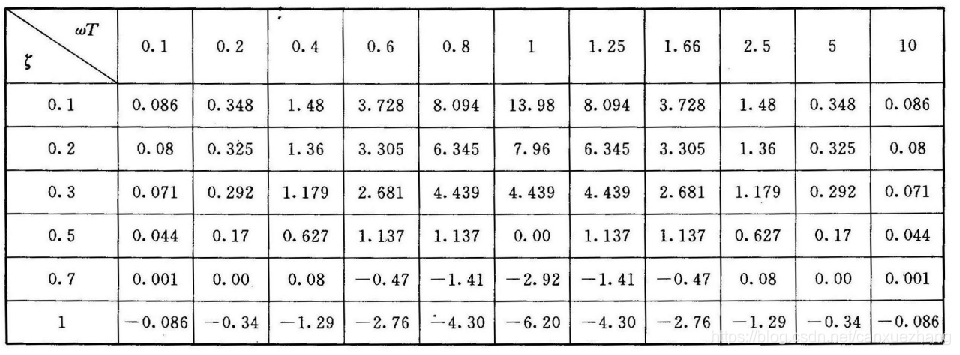

表 二阶振荡环节对数相频特性曲线角度值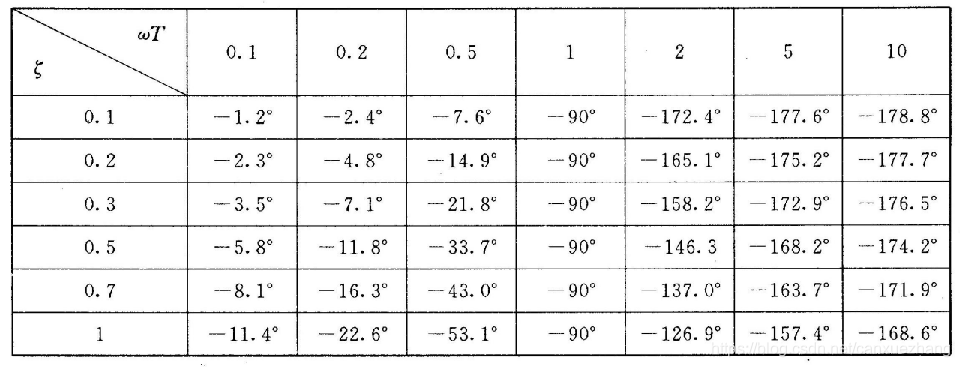



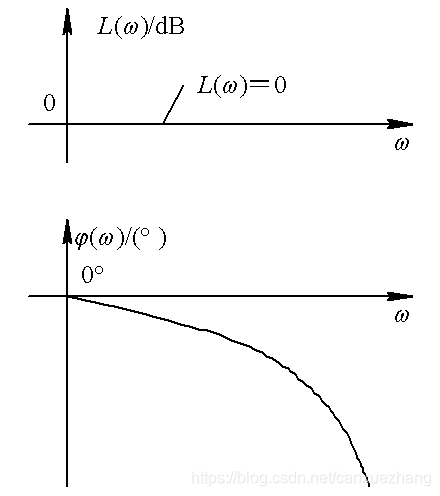
图 迟后环节的伯德图

控制系统开环频率特性伯德图的绘制

例子在另一篇文章里。

最小相位系统

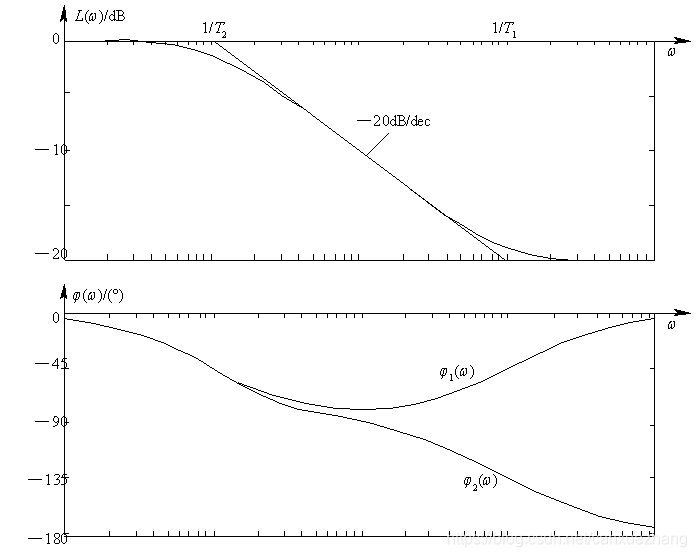
图 5-31 最小相位系统和非最小相位系统的伯德图

对数频率稳定判据

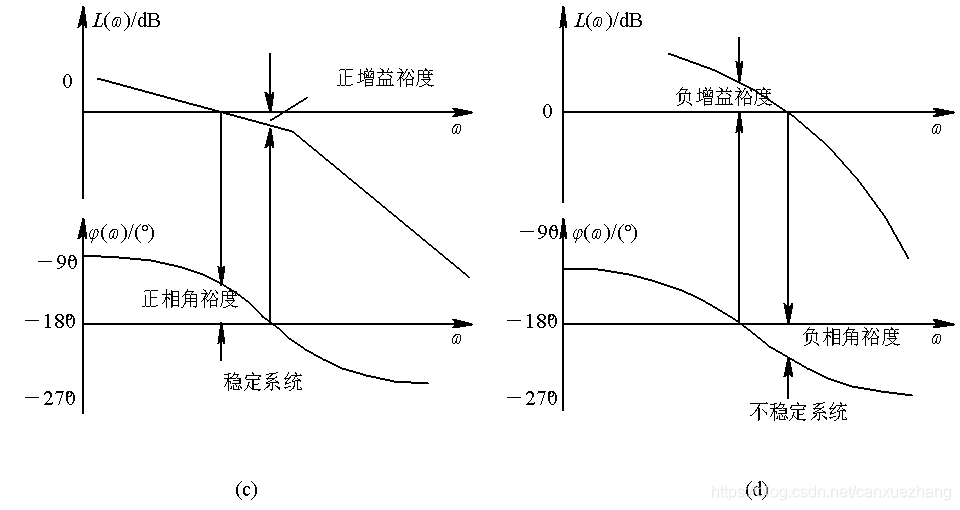
稳 定 裕 度

图 5-45 相角裕度和增益裕度

增益裕度Kg

频率响应法

闭环频率特性与开环频率特性的关系

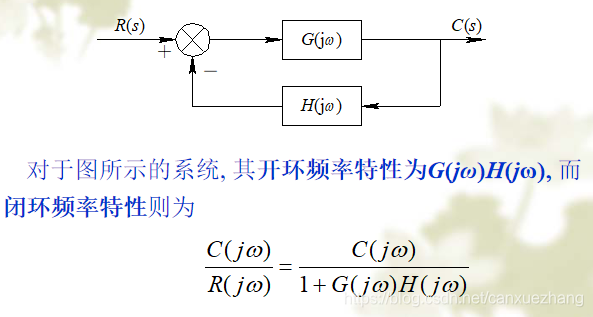
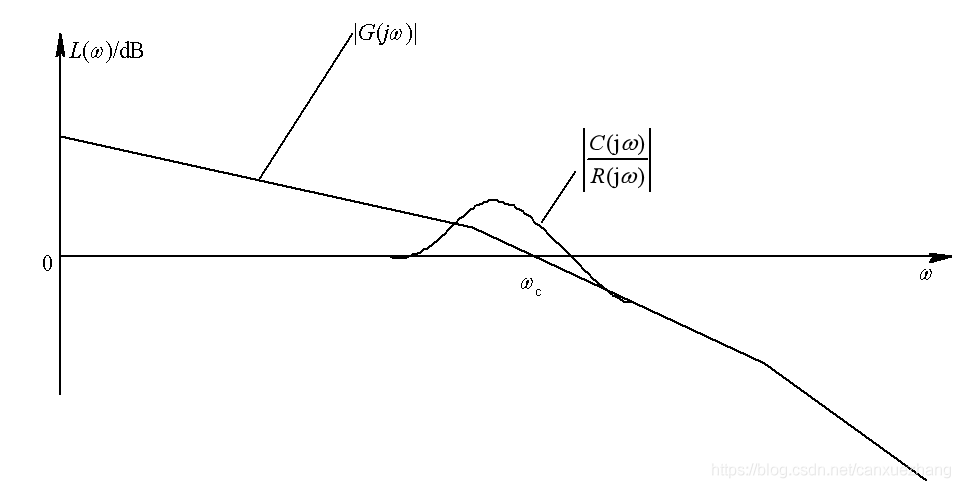
图 闭环幅频特性

闭环系统频域性能指标

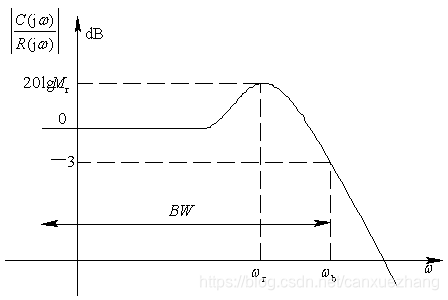
闭环频域性能指标与时域性能指标的关系

谐振峰值Mr和时域超调量Mp之间的关系

谐振频率ωr 与峰值时间tp的关系

闭环截止频率ωb 与过渡过程时间ts的关系

开环频率特性与时域响应的关系

低频段

中频段

高频段

控制系统的设计和校正

校正的基本概念

系统的性能指标

时域性能指标

频域性能指标

系统的校正方式

串联校正

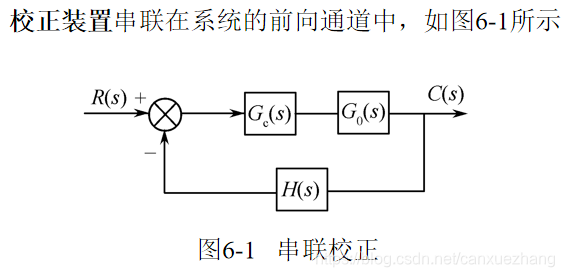
反馈（并联）校正

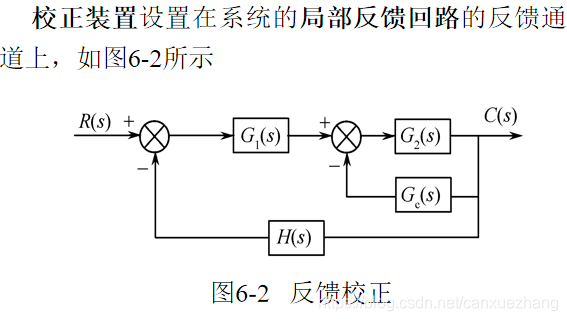
前置校正

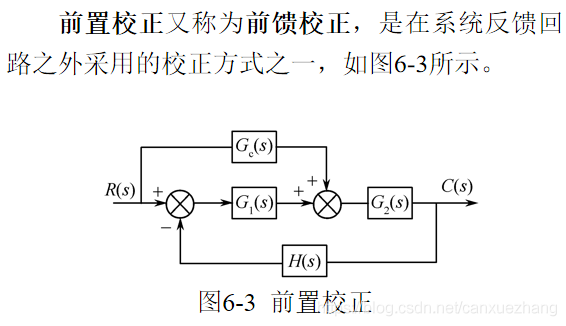
干扰补偿

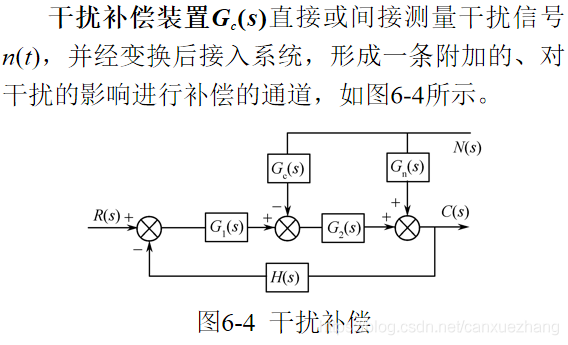
超前校正装置

滞后校正装置

滞后-超前校正装置

校正装置及其特性

超前校正装置

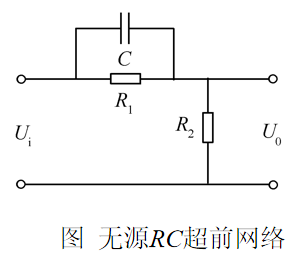
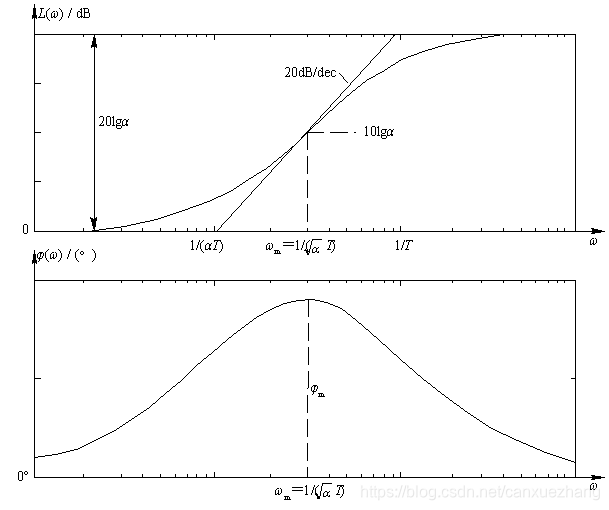
图6 超前网络的Bode图

相频曲线具有正相角，即网络的稳态输出在相位上超前于输入，故称为超前校正网络。

频率法进行串联校正

串联相位超前校正

滞后校正装置

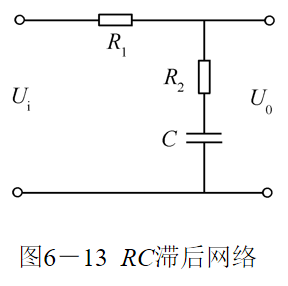
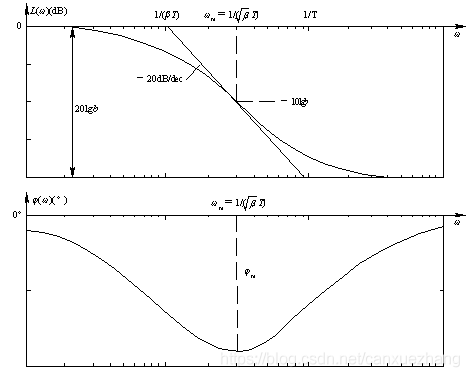
由于传递函数分母的时间常数大于分子的时间常数, 所以其幅频特性具有负斜率段, 相频特性出现负相移。
负相移表明, 校正网络在正弦信号作用下的正弦稳态输出信号, 在相位上迟后于输入信号, 所以称为迟后校正装置或迟后网络。

串联相位迟后校正

滞后校正的伯德图如下图所示。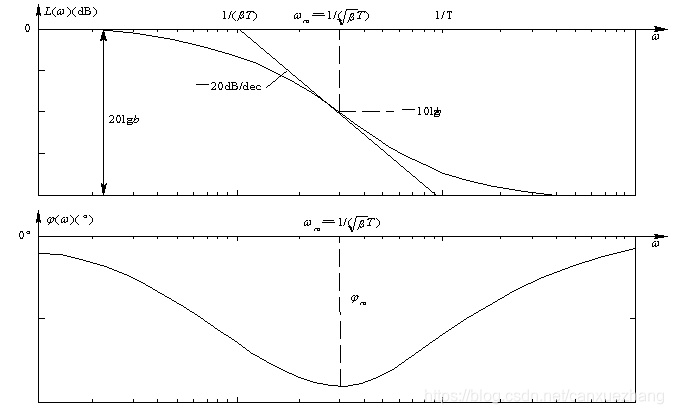

设计步骤

采样控制系统分析基础

概述

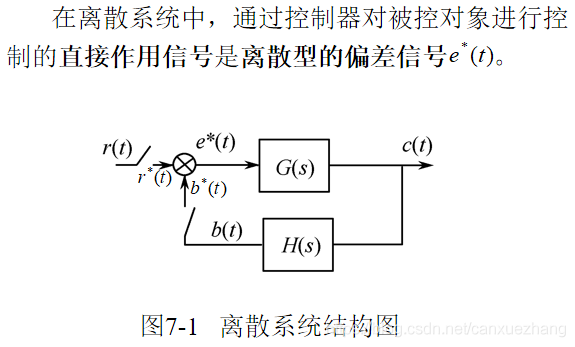
采样过程与采样定理

采样过程

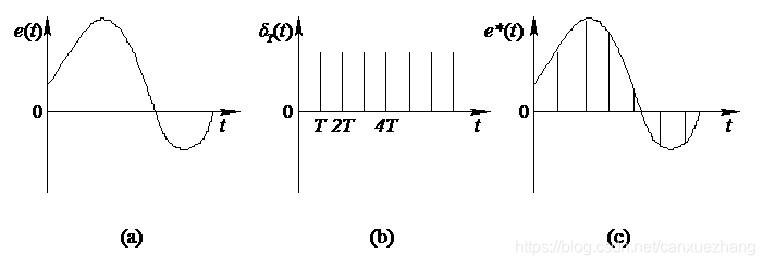
图7-6 理想采样过程

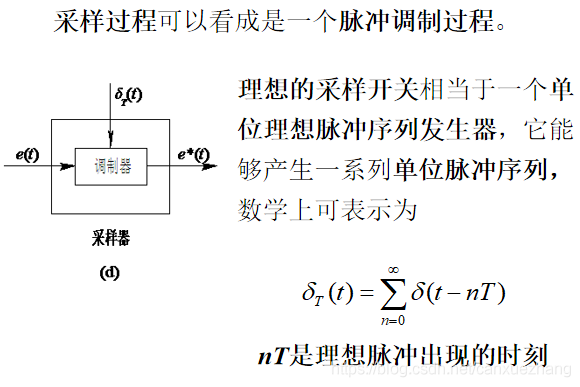
保持器

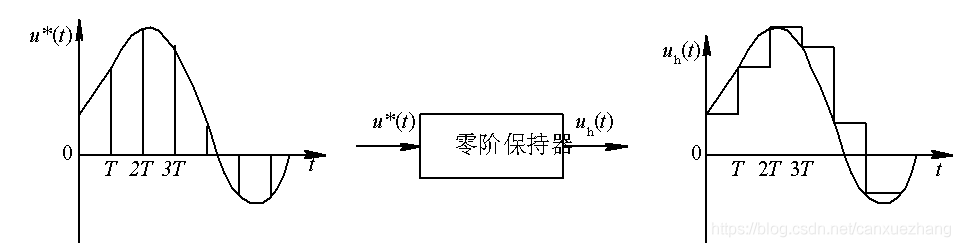
图 7-7 零阶保持器的输入和输出信号

采样定理

Z变换及反变换

Z变换定义

Z变换的基本方法

级数求和法

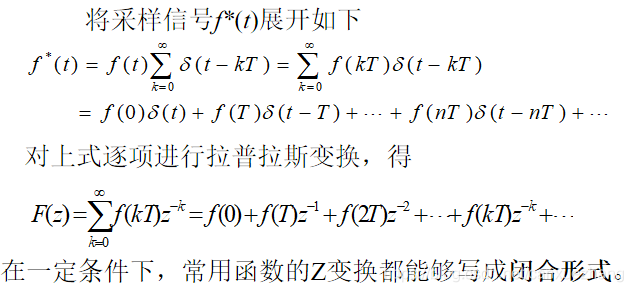
部分分式法

留数计算法（略）

Z反变换

长除法——幂级数法

部分分式法

脉冲传递函数

脉冲传递函数的基本概念

串联环节的脉冲传递函数

两个环节有采样开关时

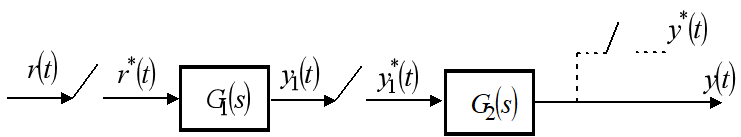
两个环节没有采样开关时

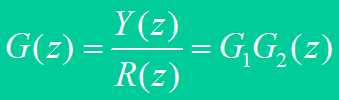
有零阶保持器时的开环系统脉冲传递函数

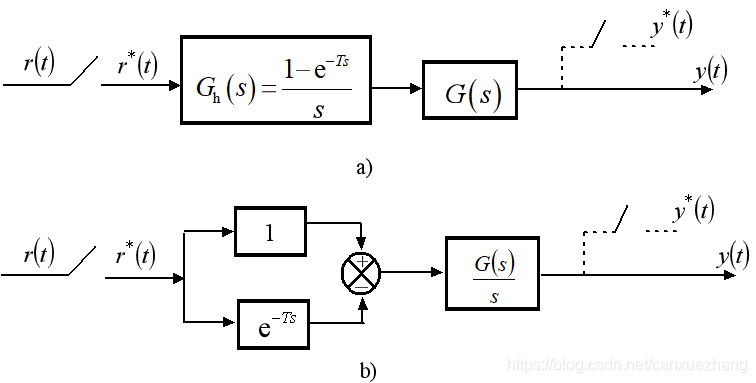
有零阶保持器时的开环采样系统

闭环系统的脉冲传递函数

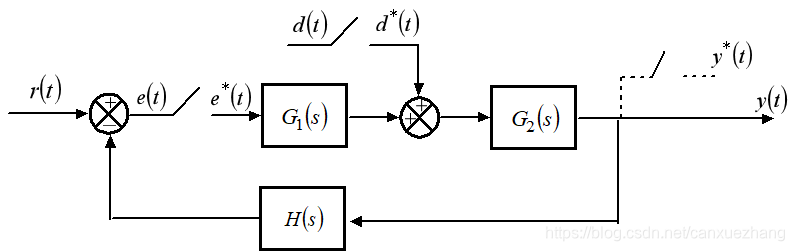
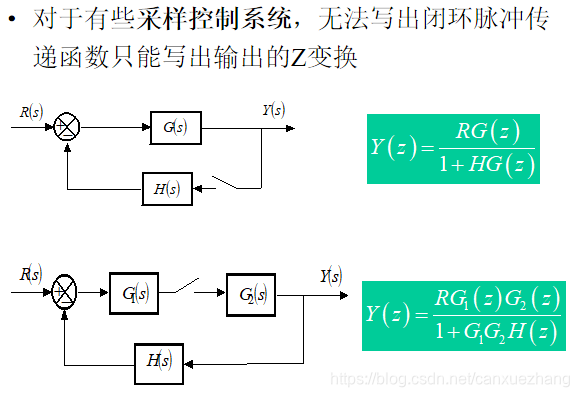
采样控制系统的性能分析

采样控制系统的稳态性能分析

s平面与z平面的映射关系

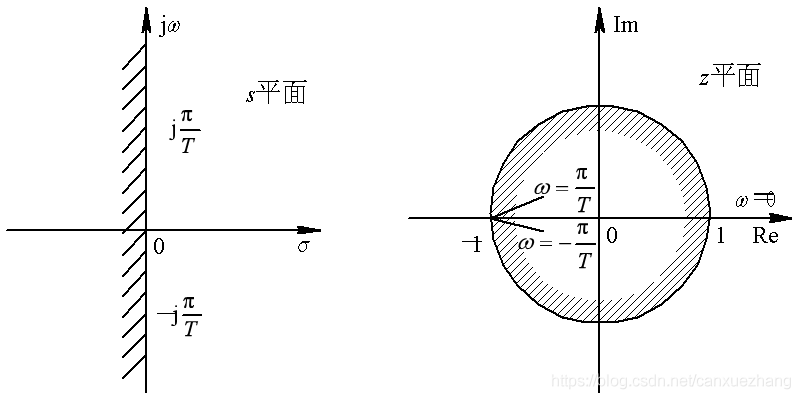
图 s平面上虚轴在z平面上的映像

稳定条件

线性采样系统劳斯判据

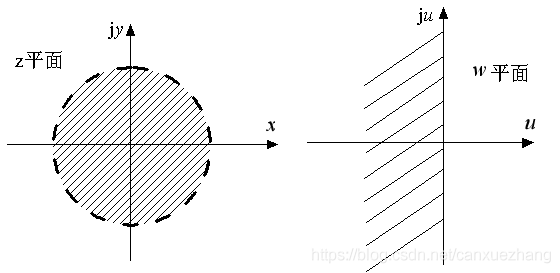
数字控制系统的稳态误差

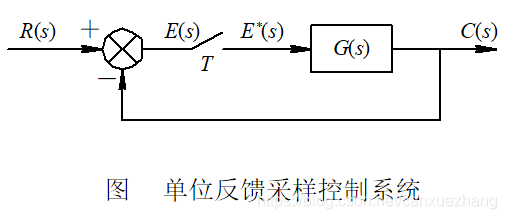
表 7-1 单位反馈离散系统的稳态误差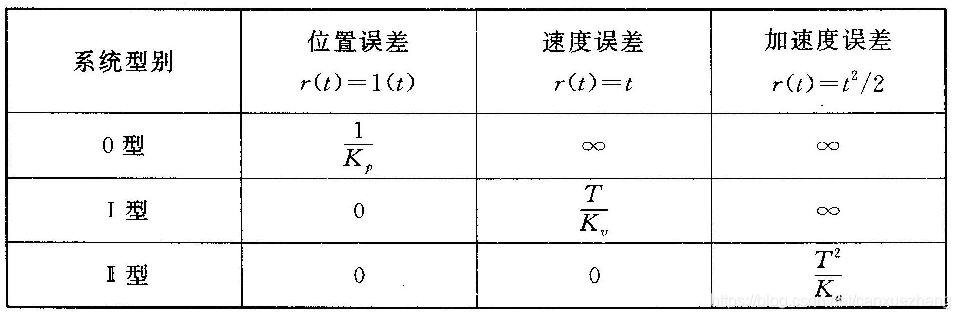

采样控制系统的动态性能分析

转载：

《自动控制原理》个人笔记（来自ppt课件）