Kosaraju 算法

Kosaraju 算法

一.算法简介

在计算科学中，Kosaraju的算法（又称为–Sharir Kosaraju算法）是一个线性时间(linear time)算法找到的有向图的强连通分量。它利用了一个事实，逆图（与各边方向相同的图形反转, transpose graph）有相同的强连通分量的原始图。

有关强连通分量的介绍在之前Tarjan 算法中：Tarjan Algorithm

逆图(Tranpose Graph ):

我们对逆图定义如下：

G^T=(V, E^T)，E^T={(u, v):(v, u)∈E}}

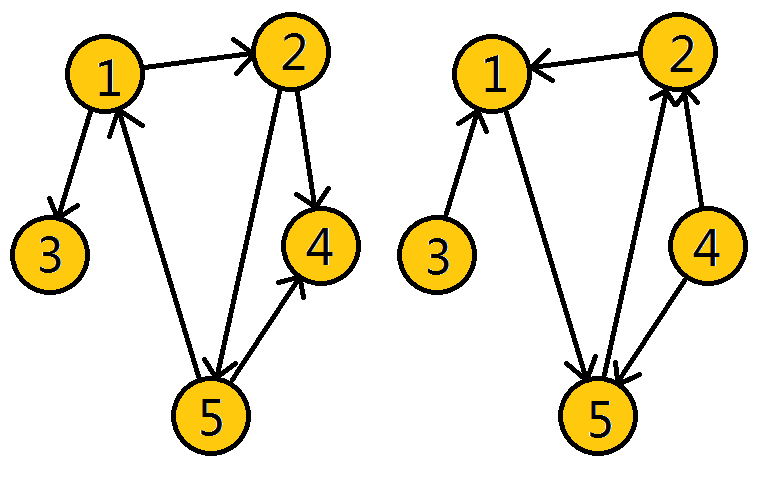
上图是有向图G ， 和图G的逆图 G^T 

摘录维基百科上对Kosaraju Algorithm 的描述：

(取自https://en.wikipedia.org/wiki/Kosaraju%27s_algorithm)

• For each vertex u of the graph, mark u as unvisited. Let L be empty.
• For each vertex u of the graph do Visit(u), where Visit(u) is the recursive subroutine:

  If u is unvisited then:

  1. Mark u as visited.
  2. For each out-neighbour v of u, do Visit(v).
  3. Prepend u to L.

  Otherwise do nothing.

• For each element u of L in order, do Assign(u,u) where Assign(u,root) is the recursive subroutine:

  If u has not been assigned to a component then:

  1. Assign u as belonging to the component whose root is root.
  2. For each in-neighbour v of u, do Assign(v,root).

  Otherwise do nothing.

通过以上的描述我们发现，Kosaraju 算法就是分别对原图G 和它的逆图 G^T 进行两遍DFS，即：

1).对原图G进行深度优先搜索，找出每个节点的完成时间(时间戳)

2).选择完成时间较大的节点开始，对逆图G^T 搜索，能够到达的点构成一个强连通分量

3).如果所有节点未被遍历，重复2). ，否则算法结束；

二.算法图示

上图是对图G,进行一遍DFS的结果，每个节点有两个时间戳，即节点的发现时间u.d和完成时间u.f

我们将完成时间较大的，按大小加入堆栈

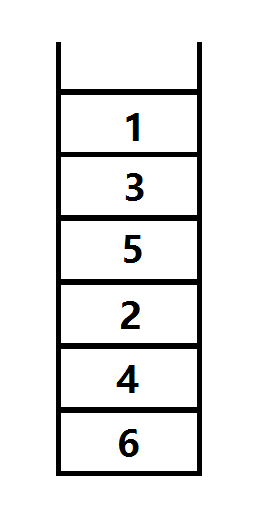
1)每次从栈顶取出元素

2)检查是否被访问过

3)若没被访问过，以该点为起点，对逆图进行深度优先遍历

4)否则返回第一步，直到栈空为止

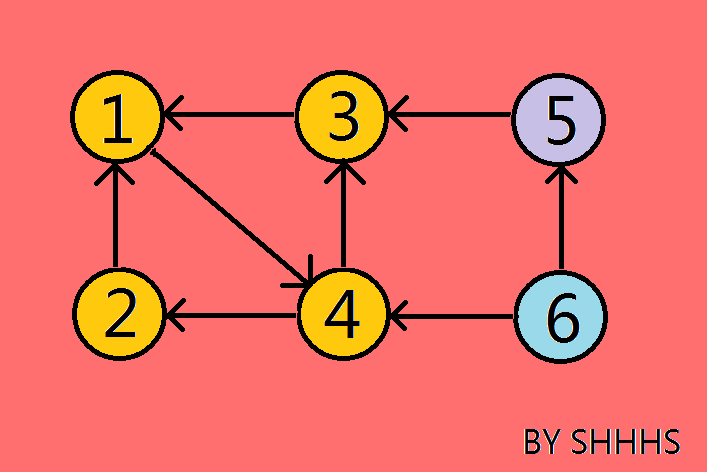
[ATTENTION] : 对逆图搜索时，从一个节点开始能搜索到的最大区块就是该点所在的强连通分量。

从节点1出发，能走到  2 ，3，4 ， 所以{1 , 2 , 3 , 4 }是一个强连通分量

从节点5出发，无路可走，所以{ 5 }是一个强连通分量

从节点6出发，无路可走，所以{ 6 }是一个强连通分量

自此Kosaraju Algorithm完毕，这个算法只需要两遍DFS即可，是一个比较易懂的求强连通分量的算法。

STRONG-CONNECTED-COMPONENTS ( GRAPH G )
1 call DFS(G) to compute finishing times u.f for each vertex u
2 compute G^T
3 call DFS (G^T) , but in the main loop of DFS , consider the vertices
         in order of decreasing u.f ( as computed in line 1 )
4 output the vertices of each tree in the depth-first forest formed in line 3 as a
         separate strongly-connected-componet

三.算法复杂度

邻接表：O(V+E)

邻接矩阵：O(V²)

该算法在实际操作中要比Tarjan算法要慢

四.算法模板&注释代码

 #include "cstdio"
 #include "iostream"
 #include "algorithm"
 
 using namespace std ;
 
 const int maxN =  , maxM = ;
 
 struct Kosaraju { int to , next ; } ;
 
 Kosaraju E[  ][ maxM ] ;
 bool vis[ maxN ];
 int head[  ][ maxN ] , cnt[  ] , ord[maxN] , size[maxN] ,color[ maxN ];
 
 int tot , dfs_num  , col_num , N , M  ;
 
 void Add_Edge( int x , int y , int _ ){//建图
          E[ _ ][ ++cnt[ _ ] ].to = y ;
          E[ _ ][ cnt[ _ ] ].next = head[ _ ][ x ] ;
          head[ _ ][ x ] = cnt[ _ ] ;
 }
 
 void DFS_1 ( int x , int _ ){
          dfs_num ++ ;//发现时间
          vis[ x ] = true ;
          for ( int i = head[ _ ][ x ] ; i ; i = E[ _ ][ i ].next ) {
                  int temp = E[ _ ][ i ].to;
                  if(vis[ temp ] == false) DFS_1 ( temp , _ ) ;
          }
          ord[(N<<) +  - (++dfs_num) ] = x ;//完成时间加入栈
 }
 
 void DFS_2 ( int x , int _ ){
          size[ tot ]++ ;// 强连通分量的大小
          vis[ x ] = false ;
          color[ x ] = col_num ;//染色
          for ( int i=head[ _ ][ x ] ; i ; i = E[ _ ][ i ].next ) {
                  int temp = E[ _ ][ i ].to;
                  if(vis[temp] == true) DFS_2(temp , _);
          }
 }
 
 int main ( ){
          scanf("%d %d" , &N , &M );
          for ( int i= ; i<=M ; ++i ){
                  int _x , _y ;
                  scanf("%d %d" , &_x , &_y ) ;
                  Add_Edge( _x , _y ,  ) ;//原图的邻接表
                  Add_Edge( _y , _x ,  ) ;//逆图的邻接表
          }
          for ( int i= ; i<=N ; ++i )
                  if ( vis[ i ]==false )
                           DFS_1 ( i ,  ) ;//原图的DFS 
 
          for ( int i =  ; i<=( N << ) ; ++i ) {
                  if( ord[ i ]!= && vis[ ord[ i ] ] ){
                           tot ++ ; //强连通分量的个数
                           col_num ++ ;//染色的颜色
                           DFS_2 ( ord[ i ] ,  ) ;
                  }
          }
 
          for ( int i= ; i<=tot ; ++i )
                  printf ("%d ",size[ i ]);
          putchar ('\n');
          for ( int i= ; i<=N ; ++i )
                  printf ("%d ",color[ i ]);
          return ;
 }

2016-09-18 00:16:19

(完)