Linux 入门记录：八、Linux 文件系统

一、文件系统

操作系统通过文件系统管理文件及数据，磁盘或分区需要创建文件系统之后，才能被操作系统所用，创建文件系统的过程又称之为格式化。没有文件系统的设备又称之为裸设备（raw），某些环境会需要裸设备，例如安装 Oracle 时会需要裸设备。

1. 常见的文件系统类型

常见的文件系统有 fat32、NTFS、ext2、ext3、ext4、xfs、HFS 等。其中，fat32 和 NTFS 是 Windows 中的文件系统，ext2、ext3、ext4、xfs、HFS 是 Linux 中的文件系统。NTFS 是当今 Windows 主流的文件系统，ext3、ext4 是 Linux 中主流的文件系统。

2. 不同文件系统之间的区别

是否带有日志
支持的分区大小
支持的单个文件大小
性能
......

二、Linux支持的文件系统

常见的有 ext2、ext3、ext4、fat(msdos)、vfat、nfs、iso9660（光盘的文件系统）、proc（Linux 内存中的虚拟文件系统）、gfs（Linux 中的 global file system，全局文件系统）、jfs （带日志的文件系统）等等，不同的 Linux 发行版本，文件系统略有不同。

三、mke2fs命令

命令 mke2fs 用来创建文件系统：

mke2fs -t ext4 /dev/sda3     给第一块 SATA 硬盘的 3 号分区创建 ext4 文件系统

常用参数：

-b blocksize   指定文件系统块大小（文件系统每次读写数据时的最小单位）

-c             建立文件系统时检查块坏损（check，检查）

-L label       打标签（类似 Windows 的磁盘卷标）

-j             建立文件系统日志（journal，日志），ext3 和 ext4 默认带日志

四、mkfs命令

命令 mkfs 也可以用来创建文件系统，相较于 mke2fs 更加简单，但是支持的参数较少，不能进行精细化的控制。

它还有一些子命令：

mkfs.ext3 /dev/sda3

mkfs.ext4 /dev/sda3

mkfs.vfat /dev/sda3

五、dumpe2fs命令

命令 dumpe2fs 可以用来查看分区的文件系统信息：

dumpe2fs /dev/sda1

六、journal日志

带日志的文件系统（ext3、ext4）拥有较强的稳定性，主要体现在出错时可以恢复。

使用带日志的文件系统，文件系统会使用一个叫做“两阶段提交”的方式进行磁盘操作，当进行磁盘操作时，文件系统进行以下操作：

文件系统将准备执行的事务的具体内容写入日志
文件系统进行操作
操作成功后，将事务的具体内容从日志删除

这样做的好处是，当事务执行的时候如果出现意外（如断电或磁盘故障），可以通过查询日志进行恢复操作。缺点是会丧失一定的性能（额外的日志读写操作）。

七、e2label命令

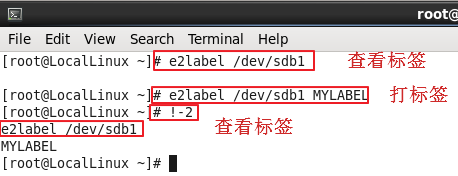
命令 e2label 可以用来为文件系统打标签：

e2label /dev/sda2           显示 sda2 的标签

e2label /dev/sda2 MYLABEL   将 sda2 的标签设置为 MYLABEL

八、fsck命令

命令 fsck 用来检查并修复坏损的文件系统：

fsck /dev/sda2

使用 -y 参数不提示而直接进行修复
默认 fsck 会自动判断文件系统类型，如果文件系统损坏比较严重，请使用 -t 参数指定文件系统类型
对于识别为文件的损坏数据（文件系统无记录），fsck 会将该文件放入 lost+found 目录
系统启动时会对磁盘进行 fsck 操作