【OpenJudge9277】【递推】Logs Stacking堆木头

Logs Stacking堆木头

总时间限制: 1000ms 内存限制: 131072kB

【描述】

Daxinganling produces a lot of timber. Before loading onto trains, the timberjacks will place the logs to some place in the open air first. Looking from the sideway, the figure of a logs stack is as follows: 
We have known that the number of logs in each layer is fewer than the lower layer for at least one log, and that in each layer the logs are connected in a line. In the figure above, there are 12 logs in the bottom layer of the stack. Now, given the number of logs in the bottom layer, the timberjacks want to know how many possible figures there may be. 
给出在最底层的木头的个数，问有多少种堆放木头的方式，当然你的堆放方式不能让木头掉下来. 
在堆放的时候木头必须互相挨着在一起.

【输入】

The first line of input contains the number of test cases T (1 <= T <= 1000000). Then T lines follow. Every line only contains a number n (1 <= n <= 200000) representing the number of logs in the bottom layer.

【输出】

For each test case in the input, you should output the corresponding number of possible figures. Because the number may be very large, just output the number mod 10^5.

【样例输入】

4
1
2
3
5

【样例输出】

1
2
5
34

【Solution】

　　用dp[i]表示底层数为i的总方案数。

　　我们可以发现，当底层数为i，上一层要放j个木头的时候，一共有(i-j)种情况。举个例子，当底层为5准备放2个木头时共有一下5-2=3种情况：

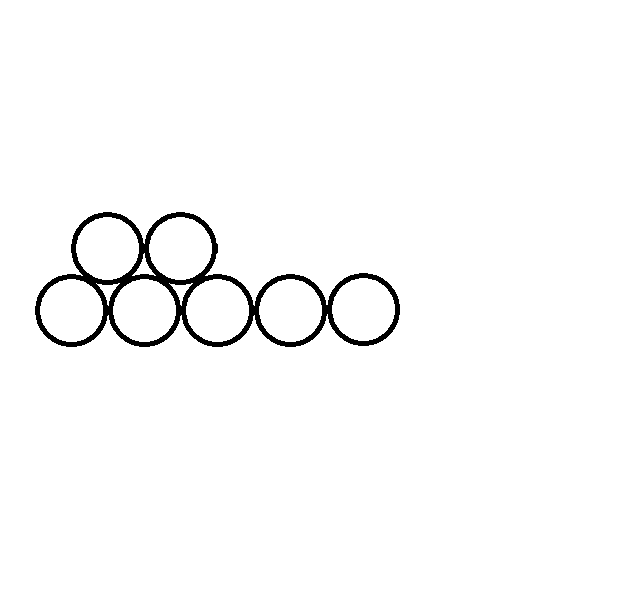
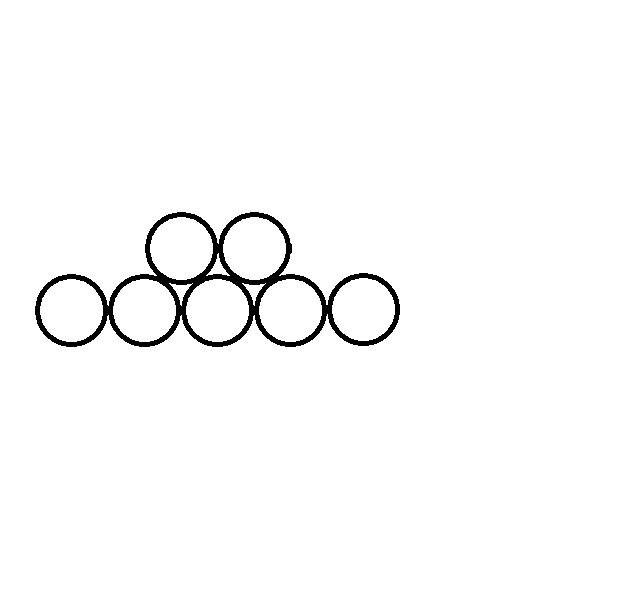
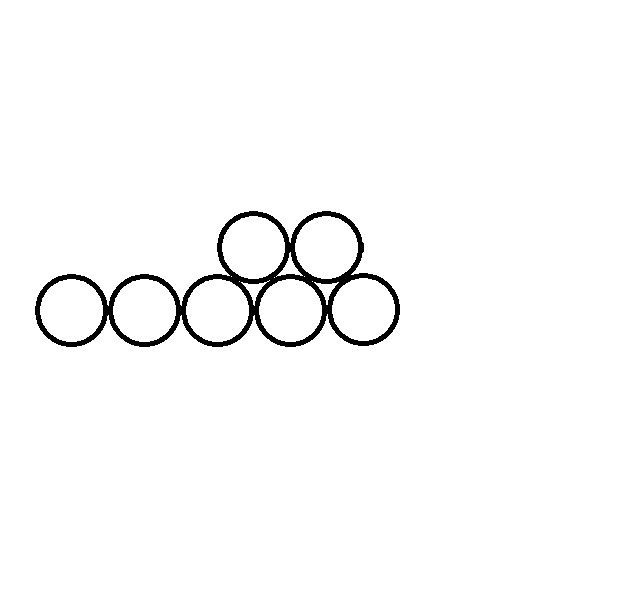
　　所以我们可以得到一个状态转移方程式：dp[i]=dp[i-1]*(i-(i-1))+dp[i-2]*(i-(i-2))+...+dp[1]*(i-1)+1。这个转移方程可以理解为枚举所有可以往基层上一层放木头的可能性，把所有的可能方案相加。

　　于是我就傻乎乎的N2算了一波，结果TLE（内心：这么性感的程序你还给我TLE？？？）。怎么优化到N呢？拿dp[4]和dp[5]做例子:

　　dp[4]=dp[3]*1+dp[2]*2+dp[1]*3+1

　　dp[5]=dp[4]*1+dp[3]*2+dp[2]*3+dp[1]*4+1

　　注意红色的部分，我们发现dp[5]比dp[4]多了一个dp[1]+dp[2]+dp[3]+dp[4],我们会发现dp[i]比dp[i-1]多一个dp[1]+dp[2]+...+dp[i-1]。

看到这里应该都能想到优化方案——用前缀和优化，这道题就A啦。

　　AC代码：

　　

 #include <cstdio>
 int T,N;
 int dp[],sum[];
 int main(){
     scanf("%d",&T);
     while(T--){
         scanf("%d",&N); dp[]=sum[]=;
         for(int i=;i<=N;++i){
             dp[i]=(dp[i-]%+sum[i-]%)%;
             sum[i]=(sum[i-]%+dp[i]%)%;
         }
         printf("%d\n",dp[N]%);
     }
     return ;
 }