洛谷mNOIP模拟赛Day2-星空

题目背景

pdf题面和大样例链接：http://pan.baidu.com/s/1cawM7c 密码：xgxv

命运偷走如果只留下结果， 时间偷走初衷只留下了苦衷。
你来过，然后你走后，只留下星空。

题目描述

逃不掉的那一天还是来了，小 F 看着夜空发呆。

天上空荡荡的，没有一颗星星——大概是因为天上吹不散的乌云吧。

心里吹不散的乌云，就让它在那里吧，反正也没有机会去改变什么了。

小 C 拿来了一长串星型小灯泡，假装是星星，递给小 F，想让小 F 开心一点。不过，有 着强迫症的小 F 发现，这串一共 n 个灯泡的灯泡串上有 k 个灯泡没有被点亮。小 F 决定 和小 C 一起把这个灯泡串全部点亮。

不过，也许是因为过于笨拙，小 F 只能将其中连续一段的灯泡状态给翻转——点亮暗灯 泡，熄灭亮灯泡。经过摸索，小 F 发现他一共能够翻转 m 种长度的灯泡段中灯泡的状态。

小 C 和小 F 最终花了很长很长很长很长很长很长的时间把所有灯泡给全部点亮了。他 们想知道他们是不是蠢了，因此他们找到了你，让你帮忙算算：在最优的情况下，至少需要 几次操作才能把整个灯泡串给点亮？

输入输出格式

输入格式：

从标准输入中读入数据。

输入第 1 行三个正整数 n,k,m。

输入第 2 行 kk 个正整数，第 i 个数表示第 i 个被没点亮的灯泡的位置 a_iai​。

输入第 3 行 mm 个正整数，第 i 个数表示第 i 种操作的长度 b_ibi​。

保证所有 b_ibi​ 互不相同；保证对于 1 \le i < k1≤i<k，有 a_i< a_i+1ai​<ai​+1；保证输入数据有解。

输出格式：

输出标准输入中。

输出一行一个非负整数，表示最少操作次数。

输入输出样例

输入样例#1： 复制

5 2 2
1 5
3 4

输出样例#1： 复制

2

说明

【样例 1 解释】

【数据范围与约定】

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解 决一部分测试数据。

每个测试点的数据规模及特点如下表

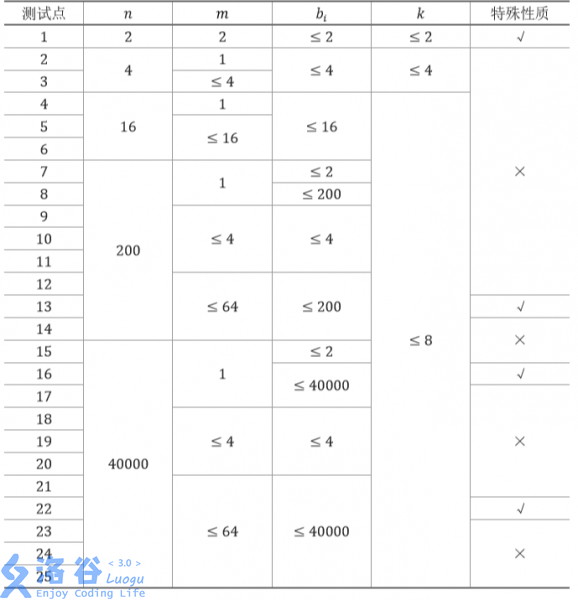
特殊性质：保证答案小于 4

---

不妨就暴力一点吧。。。

 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 #include<map>
 #include<set>
 #include<queue>
 #include<vector>
 #define INF 0x7f7f7f7f
 #define pii pair<int,int>
 #define ll long long
 #define MOD 19260817
 using namespace std;
 int read(){
     int x=,f=;char ch=getchar();
     while(ch<''||ch>''){if('-'==ch)f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 struct Node{
     int cost;
     int sum;
     int a[];
     Node(int p1=,int p2=,int b[]={}){
         cost=p1;
         sum=p2;
         memcpy(a,b,sizeof(a));
     }
 };
 ll hash(Node t){
     ll ret=;
     for(int i=;i<=;i++){
         ret=((ret<<)+t.a[i])%MOD;
     }
     return ret;
 }
 set<ll> s;
 int n,k,m;
 int L[];
 queue<Node> q;
 void init(){
     n=read(),k=read(),m=read();
     int t[]={};
     for(int i=;i<=k;i++){
         t[read()]=;
     }
     for(int i=;i<=m;i++){
         L[i]=read();
     }
     q.push(Node(,k,t));
     s.insert(hash(Node(,k,t)));
 }
 void solve(){
     while(!q.empty()){
         int a[]={};
         int cost=q.front().cost;
         int sum=q.front().sum;
         memcpy(a,q.front().a,sizeof(a));
         q.pop();
         for(int i=;i<=m;i++){
             for(int j=;j<=n-L[i]+;j++){
                 int b[]={},dsum=sum;
                 memcpy(b,a,sizeof(b));
                 for(int l=j;l<=j+L[i]-;l++){
                     if(!b[l]){
                         dsum++;
                     }
                     else{
                         dsum--;
                     }
                     b[l]=(!b[l]);
                 }
                 if(!dsum){
                     printf("%d\n",cost+);
                     return;
                 }
                 Node t=Node(cost+,dsum,b);
                 ll h=hash(t);
                 if(s.count(h)){
                     continue;
                 }
                 q.push(t);
                 s.insert(h);
             }
         }
     }
 }
 int main()
 {
 //    freopen("starlit2.in","r",stdin);
     init();
     solve();
     return ;
 }

太暴力啦QAQ

考虑正解：

首先我们知道异或满足差分的性质：可逆性

从本质上来说，异或就是取反的过程，所以正过来可以，反过去也是可以了

这样就把一段区间取反转化为端点取反了。

问题转化为：

给定一个长度为n的0-1序列，最多包含2k个1，每次可以把间隔一定长度的两个位置取反，求最少多少次把序列全部变成0

然后我们发现，肯定是要对1操作的，不可能平白无故地把两个0取反（尽管最后的结果与操作顺序无关，但这里考虑下操作顺序）

如果是1和0的话，就可以看成1转移到了0的位置并花费了一次操作的代价

如果是1和1的话，就可以看成1转移到了另一个1的位置，然后两个1都消去了并花费了一次操作的代价

这样问题转化为：

给定一个长度为n的0-1序列，最多包含2k个1，每次可以把1转移到相距一定长度的位置，如果两个1在同一位置就会消去，求最少多少次把序列全部变成0

进一步转化为：

给定一个n个节点的图，其中最多2k的节点有物品，每次可以把一件物品转移到相距一定长度的位置，如果一个节点出现两个物品就会消去，求最少多少次把物品全部消除

我们可以用2k次bfs处理出每个物品与另外所有物品消去的代价，

这样问题转化为：

给定2k个物品，其中每2个物品消去都会消耗一定的代价，求把所有物品消去的最小代价

这样就是状压dp了，可以用SPFA来解决

 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 #include<cstring>
 #include<vector>
 #include<queue>
 #define MAXK 9
 #define MAXN 40005
 #define pii pair<int,int>
 using namespace std;
 int read(){
     int x=;char ch=getchar();
     while(ch<''||ch>''){ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+(ch^);ch=getchar();}
     return x;
 }
 int n,k,m;
 int a[MAXN],b[MAXN],ed[MAXN];
 int Cost[MAXK<<][MAXK<<];
 int cnt;
 int len[];
 vector<int> v;
 void init(){
     n=read();k=read();m=read();
     for(int i=;i<=k;i++){
         a[read()]=;
     }
     n++;
     for(int i=;i<=n;i++){
         b[i]=a[i]^a[i-];
     }
     for(int i=;i<=n;i++){
         if(b[i]){
             b[i]=(++cnt);
             v.push_back(i);
         }
     }
     for(int i=;i<=m;i++){
         len[i]=read();
     }
 }
 queue<pii> q;
 void bfs(){
     memset(Cost,-,sizeof(Cost));
     for(int z=;z<v.size();z++){
         int x=v[z];
         memset(ed,-,sizeof(ed));
         while(!q.empty()) q.pop();
         q.push(make_pair(x,));
         ed[x]=;
         while(!q.empty()){
             int t=q.front().first;
             int c=q.front().second;
             q.pop();
             for(int i=;i<=m;i++){
                 for(int j=-;j<=;j+=){
                     int dt=t+j*len[i];
                     if(<=dt&&dt<=n&&-==ed[dt]){
                         ed[dt]=c+;
                         if(b[dt]){
                             Cost[b[x]][b[dt]]=ed[dt];
                         }
                         q.push(make_pair(dt,ed[dt]));
                     }
                 }
             }
         }
     }
 }
 queue<int> Q;
 int dp[<<(MAXK*)];
 int used[<<(MAXK*)];
 void solve(){
     memset(dp,0x7f,sizeof(dp));
     dp[(<<cnt)-]=;
     Q.push((<<cnt)-);
     used[(<<cnt)-]=;
     while(!Q.empty()){
         int t=Q.front();
         Q.pop();
         used[t]=;
         for(int i=;i<cnt;i++){
             if((t>>(i-))&){
                 for(int j=i+;j<=cnt;j++){
                     if((t>>(j-))&){
                         int dt=t;
                         dt^=(<<(i-));
                         dt^=(<<(j-));
                         if(Cost[i][j]!=-&&dp[dt]>dp[t]+Cost[i][j]){
                             dp[dt]=dp[t]+Cost[i][j];
                             if(!used[dt]){
                                 Q.push(dt);
                                 used[dt]=;
                             }
                         }
                     }
                 }
             }
         }
     }
     printf("%d\n",dp[]);
 }
 int main()
 {
 //    freopen("a.in","r",stdin);
 //    freopen("a.out","w",stdout);
     init();
     bfs();
     solve();
     return ;
 }

AC

以上为正解思路，这也揭示了题目的本质

总结：很好的一道题，考察较高的思维能力