Class Activation Mapping (CAM)

目录

• 概
• 主要内容
• CAM
• Grad-CAM
• Grad-CAM++
• Score-CAM
  • 最后
• 代码

Zhou B., Khosla A., Lapedriza A., Oliva A. and Torralba A. Learning Deep Features for Discriminative Localization. CVPR, 2016.

Selvaraju R., Das A., Vedantam R>, Cogswell M., Parikh D. and Batra D.Grad-CAM: Why did you say that? Visual Explanations from Deep Networks via Gradient-based Localization. ICCV, 2017.

Chattopadhyay A., Sarkar A. and Balasubramanian V. Grad-CAM++: Improved Visual Explanations for Deep Convolutional Networks. IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, 2018.

Wang H., Wang Z., Mardziel P., Hu X., Yang F., Du M., Ding S. and Zhang Z.Score-CAM: Score-Weighted Visual Explanations for Convolutional Neural Networks. CVPR, workshop, 2020.

概

CAM (class activation mapping) 是一种非常实用的可视化方法, 同时在弱监督学习中(如VQA)起了举足轻重的作用.

主要内容

CAM的概念, 用于解释, 为什么神经网络能够这么有效, 而它究竟关注了什么?

符号	说明
\(f(\cdot)\)	网络
\(X\)	网络输入
\(A_l^k\)	第\(l\)层的第\(k\)张特征图(特指在卷积层中)
\(w\)	权重
\(c\)	所关心的类别
\(\alpha\)	用于CAM的权重

CAM

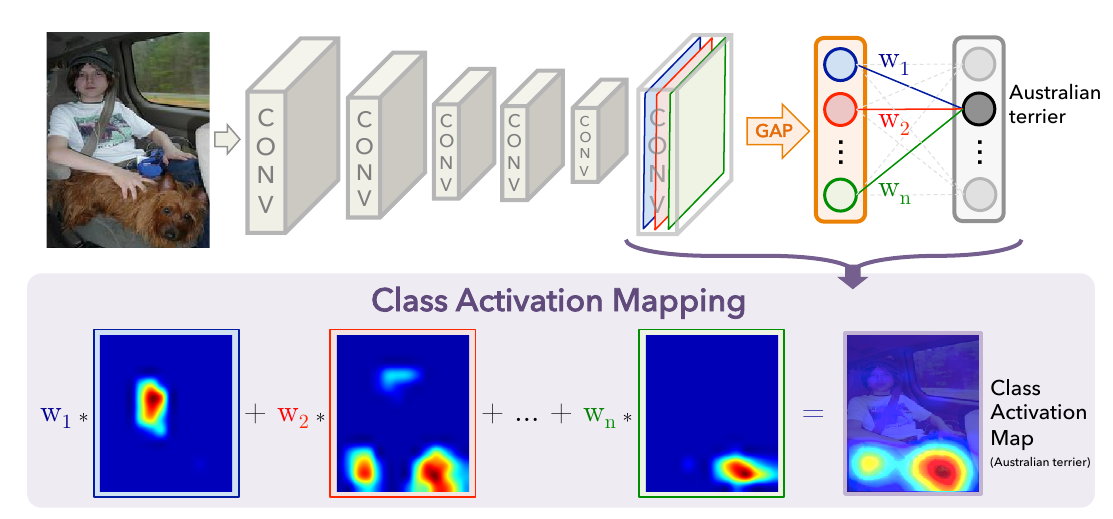
最开始的CAM仅用于特殊的CNN: 卷积层 + AvgPool + FC的结构,

设最后一层卷积层的特征图为\(A_L\), 则

\[f_c(X) = {w^c}^T GP(A_L), [GP(A_L)]_k = \frac{1}{HW}\sum_i^H \sum_j^W [A_L^k]_{ij}, k=1,\cdots, K.
\]

进一步可以注意到,

\[f_c(X) = \frac{1}{HW} \sum_i^H \sum_j^W [\sum_{k=1}^K w_k^c [A_L^k]_{ij}].
\]

于是可以定义:

\[[L_{CAM}^c]_{ij} = \sum_{k=1}^K \alpha_k^c [A_L^k]_{ij}, \quad i=1,\cdots H, j=1,\cdots, W.
\]

这里, \(\alpha = \frac{w}{HW}\).

即

\[L_{CAM}^c = \sum_{k=1}^K \alpha_k^c A_L^k.
\]

一般, 这种score会最后加个relu:

\[L_{CAM}^c = \mathrm{ReLU}(\sum_{k=1}^K \alpha_k^c A_L^k).
\]

Grad-CAM

普通的CAM有限制, Grad-CAM在此基础上进行扩展.

\[L_{Grad-CAM}^c = \mathrm{ReLU}(\sum_{k=1}^K \alpha_k^c A_l^k),
\]

\[\alpha_k^c = GP(\frac{\partial f^c}{\partial A_l^k})=\frac{1}{HW}\sum_i \sum_j \frac{\partial f_c}{\partial [A_l^k]_{ij}}.
\]

注意: \(L \rightarrow l\).

Grad-CAM++

作者认为, Grad-CAM++不能很好应对多个目标的情况, 应该进一步加权:

\[\alpha_k^c = \frac{1}{HW} \sum_i \sum_j \alpha_{ij}^{kc} \mathrm{ReLU}(\frac{\partial f_c}{\partial [A_{l}^k]_{ij}}),
\]

\[\alpha_{ij}^{kc}=\frac{\frac{\partial^2 f_c}{(\partial[A_{l}^k]_{ij})^2}}{2\frac{\partial^2 f_c}{(\partial[A_{l}^k]_{ij})^2}+\sum_i\sum_j[A_l^k]_{ij}\frac{\partial^3 f_c}{(\partial[A_{l}^k]_{ij})^3}}.
\]

Score-CAM

作者认为, 利用梯度计算score并不是一个很好的主意.

\[\alpha_k^c = f_c(X \circ H_l^k) - f(X_b),
\]

这里\(X_b\)是一个固定的基准向量, 作者直接取\(f(X_b)=\mathbb{0}\),

\[H_l^k = s(Up(A_l^k)),
\]

为将\(A_l^k\)上采样至和\(X\)相同大小, 并标准化:

\[s(M) = \frac{M - \min M}{\max M - \min M},
\]

使其落于\([0, 1]\).

最后

\(L^c_*\)最后也只是\(H\times W\)的, 需要上采样到和\(X\)一样的大小.

代码

Pytorch-GradCAM

GradCAM

GradCAM++

ScoreCAM