matplotlib.pyplot 让数据可视化

1.条形图

import matplotlib.pyplot as plt
plt.style.use('ggplot')  #  使用ggplot样式来模拟ggplot2风格的图形，ggplot2是一个常用的R语言绘图包
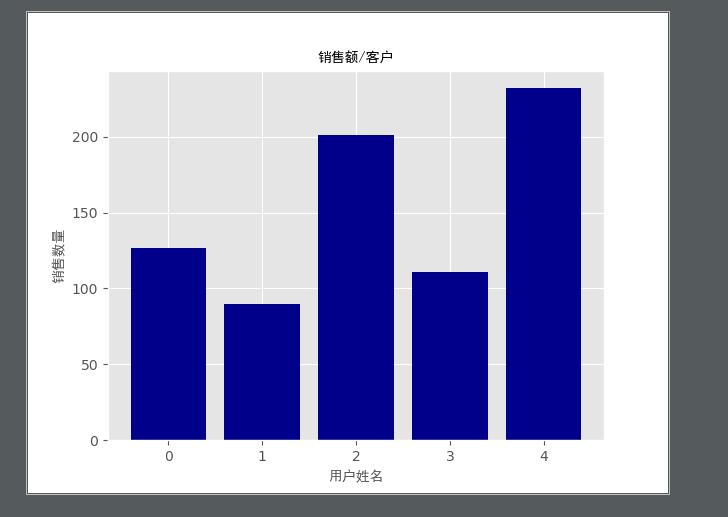
customers = ['ABC','DEF','GHI','JKL','MNO']
customers_index = range(len(customers))
sale_amounts = [127,90,201,111,232]
fig = plt.figure() #  创建基础图
ax1 = fig.add_subplot(1,1,1)  #  向基础图中添加一个子图  1,1,1表示穿件1行1列的子图，并使用第一个也是唯一的一个子图
ax1.bar(customers_index,sale_amounts,align='center',color='darkblue') # 创建条形图，customers_index设置天性左侧在x轴上的坐标,sale_amounts设置条形图的高度，align 设置条形图与标签中间对齐，color设置条形图的衍射

plt.xlabel('用户姓名', fontproperties="SimHei") #  设置X轴的标题
plt.ylabel('销售数量', fontproperties="SimHei") # 设置Y轴的标题
plt.title('销售额/客户', fontproperties="SimHei") #  设置title的标题

plt.savefig('bar_plot.png',dpi=400,bbox_inches='tight')  # 讲统计图保存在当前文件夹中，文件名为bar_plot.png，dpi=400设置图形分辨率，【每英寸（1英寸=2.54厘米）的点数】,bbox_inches='tight' 表示在保存图形时，将图形四周的空白部分去掉
plt.show() # 在一个新窗口中显示统计图，

2.直方图

# @author: erlang
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
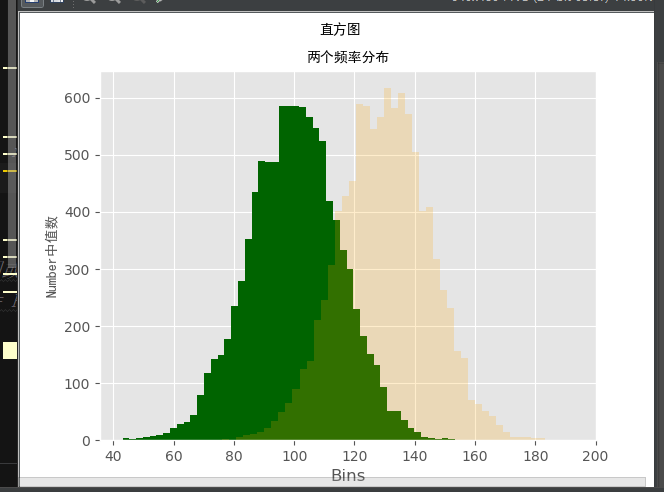
mu1,mu2,sigma = 100,130,15
x1 = mu1 + sigma * np.random.randn(10000)  # 生成两个正太分布变量x1和x2，x1的均值是100，x2的均值是130,
x2 = mu2 + sigma * np.random.randn(10000)
fig = plt.figure()
ax1 = fig.add_subplot(1,1,1)
n, bins, patches = ax1.hist(x1,bins=50,normed=False,color='darkgreen')  #创建两个柱形图或称频率分布图，bins= 50表示每个变量的值应该被分成50份
n, bins, patches = ax1.hist(x2,bins=50,normed=False,color='orange',alpha=0.2) # normed= False表示直方图显示是平率分布，而不是概率密度。alpha=0.2 表示第二个直方图应该是透明的
ax1.xaxis.set_ticks_position('bottom')
ax1.yaxis.set_ticks_position('left')
plt.xlabel('Bins')
plt.ylabel('Number中值数',fontproperties="SimHei")
fig.suptitle('直方图',fontproperties="SimHei")
ax1.set_title('两个频率分布',fontproperties="SimHei")
plt.savefig('histogram.png',dpi=400,bbox_inches='tight')
plt.show()

3.折线图

# @author: erlang
from numpy.random import randn
import matplotlib.pyplot as plt
import matplotlib
#  保证图中的中文可以正常显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False

plt.style.use('ggplot')
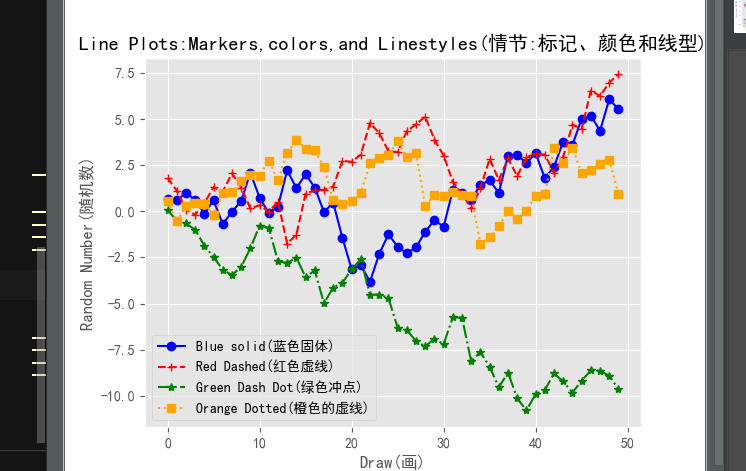
plot_data1 = randn(50).cumsum()
plot_data2 = randn(50).cumsum()
plot_data3 = randn(50).cumsum()
plot_data4 = randn(50).cumsum()

fig = plt.figure()
ax1 = fig.add_subplot(1,1,1)

# 穿件4条折线，每条折线都可以通过选项进行设置。使用不同的数据点类型、颜色和现行，label参数盘整折线在图列中可以正确标记
ax1.plot(plot_data1,marker='o',color=u'blue',linestyle='-',label='Blue solid(蓝色固体)',)
ax1.plot(plot_data2,marker='+',color=u'red',linestyle='--',label='Red Dashed(红色虚线)',)
ax1.plot(plot_data3,marker='*',color=u'green',linestyle='-.',label='Green Dash Dot(绿色冲点)',)
ax1.plot(plot_data4,marker='s',color=u'orange',linestyle=':',label='Orange Dotted(橙色的虚线)',)

ax1.xaxis.set_ticks_position('bottom')
ax1.yaxis.set_ticks_position('left')
ax1.set_title('Line Plots:Markers,colors,and Linestyles(情节:标记、颜色和线型)')
plt.xlabel('Draw(画)')  # x轴标题
plt.ylabel('Random Number(随机数)')# Y轴标题
plt.legend(loc='best') # 指示matplotlib根据图中空白部分将图列放在最合适的位置
plt.savefig('line_plot.png',dpi=400,bbox_inches='tight')
plt.show()

4散点图

# @author: erlang
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
#  保证图中的中文可以正常显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False

plt.style.use('ggplot')
x = np.arange(start=1.,stop=15.,step=1.)

y_linear = x + 5. * np.random.randn(14)
y_quadratic = x** 2 + 10. * np.random.randn(14) # 通过随机数是数据与一条直线和一条二次曲线悄悄偏离

#  使用numpy的polyfit函数通过函数两组数据点（x，y_linear）和（x，y_quadratic）拟合出一条直线和一条二次曲线
#  再使用polyid函数根据直线和二次曲线的参数与生成一个线性方程和二次方程
fn_linear = np.poly1d(np.polyfit(x,y_linear,deg=1))
fn_quadratic = np.poly1d(np.polyfit(x,y_quadratic,deg=2)) #

fig = plt.figure()
ax1 = fig.add_subplot(1,1,1)

# 代码创建带有两个回归曲线的散点图,'bo'表示（x,_y_linear）点事是蓝色圆圈,'go'表示(,x,y_quadratic)点是绿色圆圈,
# 同样'b-'表示（x,y_linear）点之间的显示一条蓝色实线 'g-'表示(,x,y_quadratic)点是绿色实线, 通过linewidth可以设置线的高度
ax1.plot(x,y_linear,'bo',x,y_quadratic,'go',x,fn_linear(x),'b-',x,fn_quadratic(x),'g-',linewidth = 2.)
ax1.xaxis.set_ticks_position('bottom')
ax1.yaxis.set_ticks_position('left')
ax1.set_title('Scatter ploys Regression Lines(散射伎俩回归直线)',)
plt.xlabel('x')
plt.ylabel('f(x)')

# 设置了x轴和Y轴的范围。这两条曲线使用min和max函数基于实际数据设置坐标轴范围，你也可以使用具体的数值设置范围，列入xlim(0,20)和ylom(0,200)
# 如果你没有设置坐标范围，那么matplotlib会替你自己设置，
plt.xlim(min(x)-1,max(x)+1)
plt.ylim(min(y_quadratic)-10.,max(y_quadratic)+10.)
plt.savefig('scatter_plot.png',dpi=400,bbox_inches='tight')
plt.show()