UVA11987 Almost Union-Find [带权并查集]

　　洛谷传送门

Almost Union-Find

题目描述

输入输出格式

输入格式：

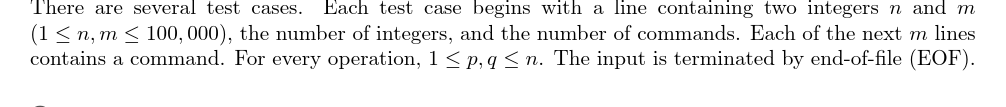
输出格式：

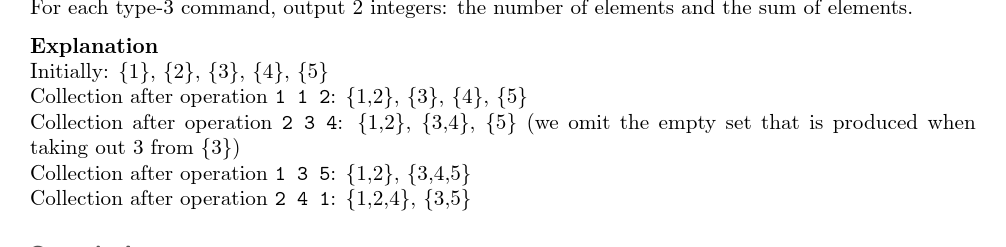
输入输出样例

输入样例#1：

5 7
1 1 2
2 3 4
1 3 5
3 4
2 4 1
3 4
3 3

输出样例#1：

3 12
3 7
2 8

---

　　分析：

　　不得不说是一道神奇的题目

　　如果只有操作1和操作3，那就是一道普通的带权并查集。然而，TM还有个毁天灭地的操作2。。。因为并查集是不支持删除操作的，所以我们得想个办法表示某一个元素在该集合中被删除。

　　这里我们用一个数组$id[i]$记录$i$节点当前的编号，如果我们删除了一个点，我们就把$id[i]$指向一个新的地址，在原本的集合中删除掉它的信息，然后把这个新的地址与要合并的集合合并。原本的点就基本可以当作是“被废弃了”，因为我们每次查找一个点的集合的时候就直接$find(id[x])$。当然，$id[x]$一开始就赋值为$x$。

　　不过貌似有巨佬用可持久化并查集$A$了，并不知道怎么用可持久化并查集做。。。。。。

　　$PS$：写了个启发式合并，读优输优，水了个最优解$hahahaha$。

　　Code：

　　

//It is made by HolseLee on 22nd Aug 2018
//UVA11987
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<iomanip>
#include<algorithm>
using namespace std;

typedef long long ll;
const int N=2e5+;
int n,m,id[N],fa[N],cnt[N],rk[N];
ll sum[N];

inline int read()
{
    char ch=getchar();int num=;bool flag=false;
    while(ch<''||ch>''){if(ch=='-')flag=true;ch=getchar();}
    while(ch>=''&&ch<=''){num=num*+ch-'';ch=getchar();}
    return flag?-num:num;
}

inline void print(int x)
{
    if(x>)print(x/);
    putchar(x%+'');
}

inline int find(int x)
{
    return fa[x]==x?x:fa[x]=find(fa[x]);
}

inline void merge(int x,int y)
{
    int fx=find(id[x]),fy=find(id[y]);
    if(rk[fx]>rk[fy]){
        fa[fy]=fx;
        sum[fx]+=sum[fy];
        cnt[fx]+=cnt[fy];
    }else{
        fa[fx]=fy;
        sum[fy]+=sum[fx];
        cnt[fy]+=cnt[fx];
        if(rk[fx]==rk[fy])rk[fy]++;
    }
}

inline void del(int x)
{
    int fx=find(id[x]);
    cnt[fx]--;sum[fx]-=(ll)x;
    id[x]=++n;
    fa[id[x]]=id[x];
    cnt[id[x]]=rk[id[x]]=;
    sum[id[x]]=(ll)x;
}

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF){
        for(int i=;i<=n;++i)fa[i]=id[i]=i,sum[i]=(ll)i,cnt[i]=rk[i]=;
        int op,x,y;
        for(int i=;i<=m;++i){
            op=read();
            switch(op){
                case :
                    x=read();y=read();
                    if(find(id[x])!=find(id[y]))merge(x,y);
                    break;
                case :
                    x=read();y=read();
                    if(find(id[x])!=find(id[y])){
                        del(x);merge(x,y);
                    }
                    break;
                case :
                    x=read();
                    print(cnt[find(id[x])]);
                    putchar(' ');
                    print(sum[find(id[x])]);
                    putchar('\n');
                    break;
            }
        }
    }
    return ;
}