[CSP-S模拟测试]:飞(fly)（数状数组+简单几何）

题目描述

$liu\_runda$决定提高一下知识水平，于是他去请教郭神。郭神随手就给了$liu\_runda$一道神题，$liu\_runda$并不会做，于是把这个题扔到联考里给高二的做。
郭神有$n$条位于第一象限内的线段，给出每条线段与$x$轴和$y$轴交点的坐标，显然这样就可以唯一确定每一条线段。
$n$条线段和$y$轴交点的纵坐标分别为$1,2,3,4...n$。我们记和$y$轴交点纵坐标为$i$的线段和$x$轴交点的横坐标为$x_i+1,x_i$按这样的方式生成：
$x_1$由输入给出。
$x_i=(x_{i-1}+a)\%mod,2\leqslant i\leqslant n$。
即：如果$x_3=4$，则与$y$轴交点纵坐标为$3$的抛物线，和$x$轴交点的横坐标为$4+1=5$。
我们保证给出的$n,x_1,a,mod$使得所有的$x_i$互不相同。
对于第一象限内的所有点（点的横纵坐标可以是任意实数），如果一个点被$x$条线段经过，它的鬼畜值就是$\frac{x\times (x-1)}{2}$。
求第一象限内的所有点的鬼畜值之和。

---

输入格式

一行$4$个整数$n,x_1,a,mod$。

---

输出格式

$1$行一个整数表示鬼畜值之和。

---

样例

样例输入1：

5 2 4 7

样例输出1：

5

样例输入2：

100000 233 23333 5026733

样例输出2：

2496173893

样例输入3：

10000000 233 8 66777383

样例输出3：

12430707670886

样例输入4：

10000000 6666 6666 30099271

样例输出4：

24993727056912

样例输入5：

10000000 23336666 100000 66777383

样例输出5：

24999931370887

---

数据范围与提示

第$1,2$个测试点，$n\leqslant 100$。
第$3,4$个测试点，$n\leqslant {10}^5$。
第$5,6$个测试点的数据，$a\leqslant 10$。
第$7,8$个测试点，$x_1=a$。
第$9,10$个测试点，无特殊限制。
对于全部数据，$1\leqslant n\leqslant {10}^7,1\leqslant a\leqslant {10}^5,1\leqslant mod\leqslant {10}^8$，$a,mod$互质，$n<mod$，给出的$n,x_1,a,mod$使得所有的$x_i$互不相同。
请选手注意，${10}^7$个$int$类型的变量将占用大约$40MB$的内存，导致内存超限，本题得$0$分。

---

题解

看到这道题，我还以为是道数论，准备弃掉，然后在认真算了一下，我就$AK$了这套卷……

首先，题目中所说的交点贡献的$\frac{x\times (x-1)}{2}$吓到了不少人，也包括我，况且点还都不是整数点，这要是爆精度不就凉了嘛。

仔细算一下便会发现，其实我们根本就不用考虑这一点，我们来化一下式子：

　　假设现在有$x$条线已经交到了一个点上，那么这个点现在的贡献显然就是$\frac{x\times (x-1)}{2}$；

　　现在又来了一条直线，交到了这个点上，那么这个点的贡献就变成了$\frac{(x+1)\times x)}{2}$；

　　将上面两个式子做差得$x$，也就是说，一条直线对一个点的贡献就等于这个点原本就有的直线的个数；

　　那么接着转化，就可以认为一条直线对答案的贡献与它与多少条直线交于一个点无关，而只与它与多少条直线相交有关。

接着就会发现，问题就可以转化为求逆序对的个数。

然后你可能会想到，$\Theta(n\log n)$求逆序对，卡卡常没准就$A$了，然而……

空间限制$32MB$，在爆零面前你选择了屈服。

那么怎么办呢？

认真阅读数据范围$ing...$

忽然发现$a$好小，考虑从$a$入手，突然发现式子$x_i=(x_{i-1}+a)\%mod$中如果不$mod$的的话就是一个等差数列，再画画图？

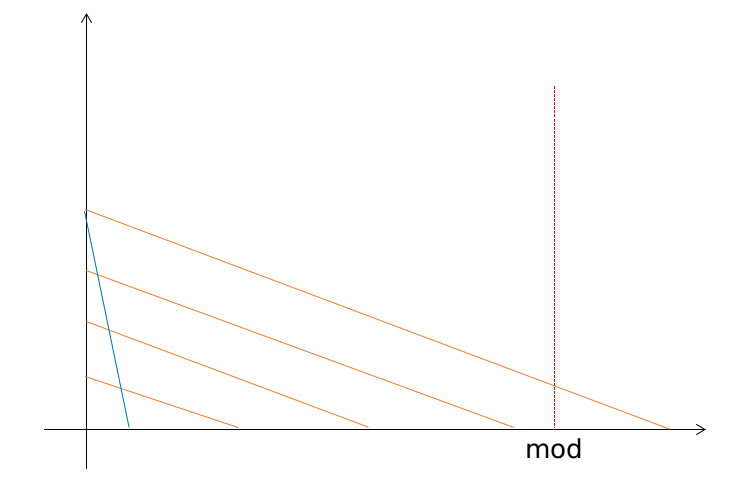
发现不超过$mod$的一组线是平行的，进而，我们可以只维护小于$a$的逆序对，剩下的通过上一位推出来就好了。

情况挺多，细节不少，详细看标程吧。

时间复杂度：$\Theta(a\log a)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n,x,a,mod;
int tr[500000];
int flag,pls,cut;
long long ans;
int lowbit(int x){return x&-x;}
void change(int x)
{
	for(int i=x;i<=a;i+=lowbit(i))
		tr[i]++;
}
int ask(int x)
{
	int res=0;
	for(int i=x;i;i-=lowbit(i))
		res+=tr[i];
	return res+1;
}
int main()
{
	scanf("%d%d%d%d",&n,&x,&a,&mod);
	if(x<a)change(x+1);
	flag=x;
	for(int i=2;i<=n;i++)
	{
		flag=(flag+a)%mod;
		if(flag<a){pls=i-ask(flag+1);cut++;change(flag+1);}
		else{if(flag<x)pls++;pls-=cut;}
		ans+=pls;
	}
	printf("%lld",ans);
	return 0;
}

---

rp++