【HDU6621】K-th Closest Distance【线段树】

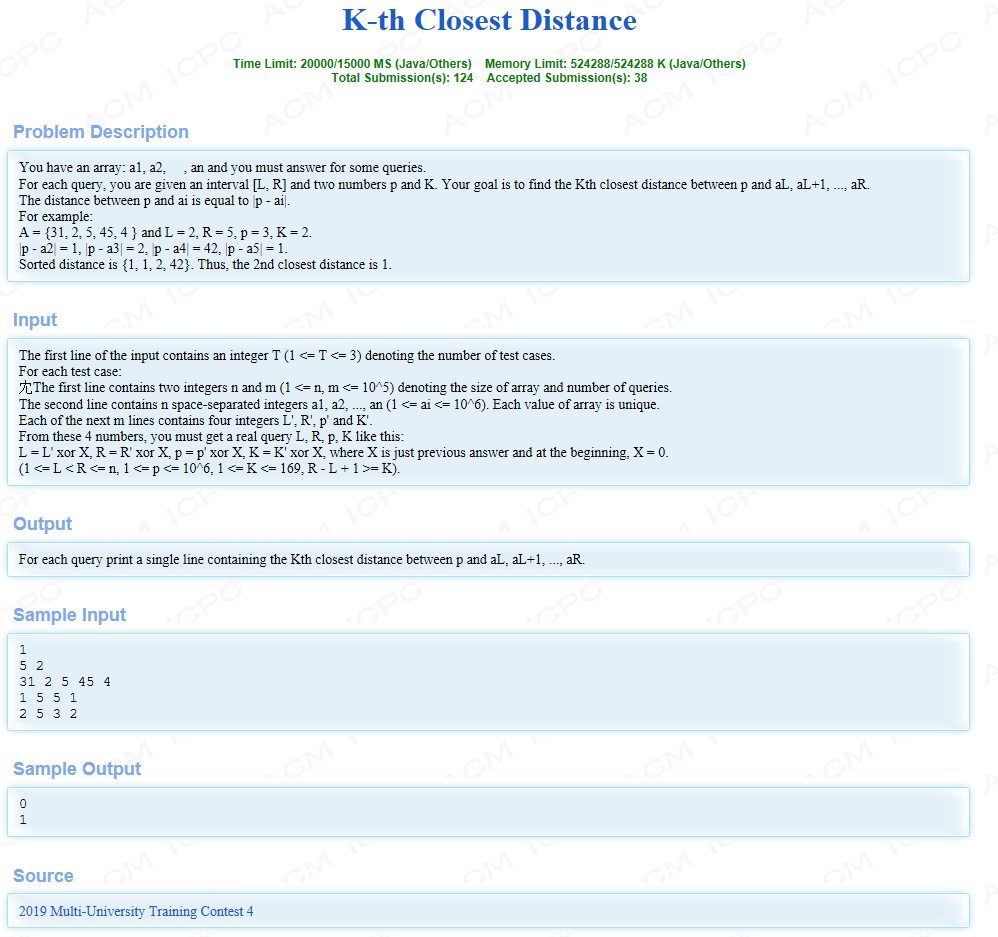
题目大意：给你一堆数，每次询问区间[l,r]中离p第k小的|ai-p|

题解：考虑二分答案，对于每个可能的答案，我们只需要看在区间[l,r]里是否有≥k个比二分的答案还要接近于p的

考虑下标线段树，并将其可持久化，线段树i存储1~i中每个数有几个

因为数比较大，考虑离散化，这样最多1e5个数，可以接受

判断时只需要查找第r棵线段树和第l-1棵线段树的区间[l,r]中位于[p-k,p+k]的数有几个然后将返回的值相减看是否≥k即可，注意这里有一些细节

时间复杂度O(mlog^2n)

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
using namespace std;
int T,n,m,ans;
struct node
{
    int v,bh;
}a[];
bool cmp(const node &T1,const node &T2){return T1.v<T2.v;}
bool cmp2(const node &T1,const node &T2){return T1.bh<T2.bh;}
int L[],R[];

int head[],lson[*],rson[*],cnt[*],tn;
void insert(int l,int r,int p,int now)
{
    if(l==r && l==p){cnt[now]++;return;}
    int mid=l+r>>;
    if(p<=mid)
    {
      tn++;
      lson[tn]=lson[lson[now]];
      rson[tn]=rson[lson[now]];
      cnt[tn]=cnt[lson[now]];
      lson[now]=tn;
      insert(l,mid,p,lson[now]);
    }
    else
    {
      tn++;
      lson[tn]=lson[rson[now]];
      rson[tn]=rson[rson[now]];
      cnt[tn]=cnt[rson[now]];
      rson[now]=tn;
      insert(mid+,r,p,rson[now]);
    }
    cnt[now]=cnt[lson[now]]+cnt[rson[now]];
}
void init()
{
    tn=;
    for(int i=;i<=n;i++)
    {
      head[i]=++tn;
      lson[head[i]]=lson[head[i-]];
      rson[head[i]]=rson[head[i-]];
      cnt[head[i]]=cnt[head[i-]];
      insert(,n,L[a[i].v],head[i]);
    }
}
int ask(int l,int r,int al,int ar,int now)
{
    if(al>ar) return ;
    if(l==al && r==ar)return cnt[now];
    int mid=l+r>>;
    if(ar<=mid)return ask(l,mid,al,ar,lson[now]);
    if(al>mid)return ask(mid+,r,al,ar,rson[now]);
    return ask(l,mid,al,mid,lson[now])+ask(mid+,r,mid+,ar,rson[now]);
}

int aa,bb,val,k;
int main()
{
    scanf("%d",&T);
    while(T--)
    {
      scanf("%d%d",&n,&m);
      memset(L,,sizeof(L));
      memset(R,,sizeof(R));
      ans=;
      for(int i=;i<=n;i++){scanf("%d",&a[i].v);a[i].bh=i;}
      sort(a+,a++n,cmp);
      for(int i=;i<=n;i++)if(!L[a[i].v])L[a[i].v]=R[a[i].v]=i;
      for(int i=;i<=;i++)if(R[i-]> && R[i]==)R[i]=R[i-];
      for(int i=;i>;i--)if(L[i+]> && L[i]==)L[i]=L[i+];
      sort(a+,a++n,cmp2);
      init();
      while(m--)
      {
        scanf("%d%d%d%d",&aa,&bb,&val,&k);
        aa^=ans;bb^=ans;val^=ans;k^=ans;
        int l=,r=,mid,tl,tr;
        while(l<r)
        {
          mid=l+r>>;
          tl=val-mid;tr=val+mid;
          tl=max(tl,);tr=min(tr,);
          if(R[tr]<L[tl] || R[tr]== || L[tl]==){l=mid+;continue;}
          int t1=ask(,n,L[tl],R[tr],head[bb]),t2=;
          if(aa>)t2=ask(,n,L[tl],R[tr],head[aa-]);
          if(t1-t2<k)l=mid+;
          else r=mid;
        }
        printf("%d\n",r);
        ans=r;
      }
    }
    return ;
}

心得：考场上很快就想到做法，但是被卡了很久，因为数组没开够。。第一次见到*200的线段树，不知道什么原因开这么大，欠缺思考

实际上*20能过，只不过考场上可能数据出锅或者评测机出锅导致没过，赛后重测过了