Lucene的FuzzyQuery中用到的Levenshtein Distance(LD)算法

2019独角兽企业重金招聘Python工程师标准>>>

Lucene的FuzzyQuery中用到的Levenshtein Distance(LD)算法 博客分类： java 搜索引擎，爬虫

主题:Levenshtein Distance(LD);

相关介绍：Levenshtein distance是由俄国科学家Vladimir Levenshtein在1965年设计并以他的名字命名的。如果不能拼写或发Levenshtein音，通常可以称它edit distance（编辑距离）；

用途：该算法用于判断两个字符串的距离，或者叫模糊度。个人理解就是差异程度。而差异的标准就是1）加一个字母(Insert),2)删一个字母(Delete),3改变一个字母(Substitute)。

算法描述：

Step	Description
1	Set n to be the length of s.Set m to be the length of t. If n = 0, return m and exit.If m = 0, return n and exit. Construct a matrix containing 0..m rows and 0..n columns.
2	Initialize the first row to 0..n. Initialize the first column to 0..m.
3	Examine each character of s (I from 1 to n).
4	Examine each character of t (j from 1 to m).
5	If s[i] equals t[j], the cost is 0. If s[i] doesn’t equal t[j], the cost is 1.
6	Set cell d[I,j] of the matrix equal to the minimum of: a. The cell immediately above plus 1: d[i-1,j] + 1. b. The cell immediately to the left plus 1: d[I,j-1] + 1. c. The cell diagonally above and to the left plus the cost: d[i-1,j-1] + cost.
7	After the iteration steps (3, 4, 5, 6) are complete, the distance is found in cell d[n,m].

1、  得到源串s长度n与目标串t的长度m，如果一方为的长度0，则返回另一方的长度。

2、  初始化(n+1)*(m+1)的矩阵d，第一行第一列的值为0增至对应的长度。

3、  遍历数组中的每一个字符(i,j从1开始)。如果s[i]与t[j]的值相等，cost值为0，否则为1。D[i][j]的值为d[i-1,j] + 1(左边的值加1)、d[I,j-1] + 1.(上边的值加1)、d[i-1,j-1] + cost (斜上角的值加cost) 中的最小者。

4、  等第三步遍历完后，右下角d[n,m]的值就为两个字符串的距离。

应用演示：source:word与target:world比较过程。

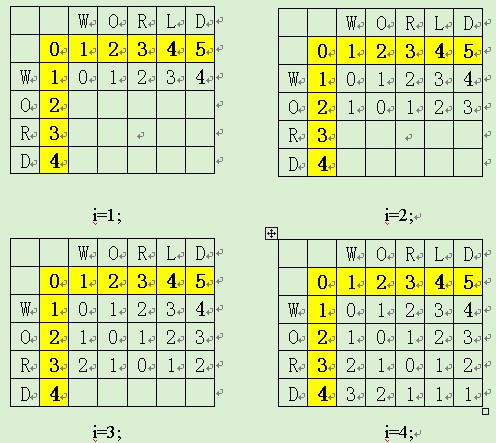
应用举例：据《开发自己的搜索引擎——Lucene 2.0+Heriterx

》记载P134页记载，lucene中FuzzyQuery(模糊匹配)就是应用该算法的；也可用于Spell checking(拼写检查),Speech recognition(语句识别),DNA analysis(DNA分析) ,Plagiarism detection(抄袭检测)。

参考资料：

http://www.merriampark.com/ld.htm

http://my.oschina.net/MrMichael/blog/339217

转载于:https://my.oschina.net/xiaominmin/blog/1597443