Intersection of Two Prisms(AOJ 1313)

• 原题如下：

  Suppose that P₁ is an infinite-height prism whose axis is parallel to the z-axis, and P₂ is also an infinite-height prism whose axis is parallel to the y-axis. P₁ is defined by the polygon C₁ which is the cross section of P₁ and the xy-plane, and P₂is also defined by the polygon C₂ which is the cross section of P₂ and the xz-plane.

  Figure I.1 shows two cross sections which appear as the first dataset in the sample input, and Figure I.2 shows the relationship between the prisms and their cross sections.

  

  Figure I.1: Cross sections of Prisms

  

  Figure I.2: Prisms and their cross sections

  

  Figure I.3: Intersection of two prisms

  Figure I.3 shows the intersection of two prisms in Figure I.2, namely, P₁ and P₂.

  Write a program which calculates the volume of the intersection of two prisms.

  Input

  The input is a sequence of datasets. The number of datasets is less than 200.

  Each dataset is formatted as follows.

  m n
  x₁₁ y₁₁
  x₁₂ y₁₂ 
  .
  .
  .
  x_1m y_1m 
  x₂₁ z₂₁
  x₂₂ z₂₂
  .
  .
  .
  x_2n z_2n

  m and n are integers (3 ≤ m ≤ 100, 3 ≤ n ≤ 100) which represent the numbers of the vertices of the polygons, C₁ and C₂, respectively.

  x_1i, y 1 i, x _2j and z _2j are integers between -100 and 100, inclusive. ( x _1i, y _1i) and ( x _2j , z _2j) mean the i-th and j-th vertices' positions of C ₁ and C ₂respectively.

  The sequences of these vertex positions are given in the counterclockwise order either on the xy-plane or the xz-plane as in Figure I.1.

  You may assume that all the polygons are convex, that is, all the interior angles of the polygons are less than 180 degrees. You may also assume that all the polygons are simple, that is, each polygon's boundary does not cross nor touch itself.

  The end of the input is indicated by a line containing two zeros.

  Output

  For each dataset, output the volume of the intersection of the two prisms, P₁ and P₂, with a decimal representation in a line.

  None of the output values may have an error greater than 0.001. The output should not contain any other extra characters.

  Sample Input

  4 3
  7 2
  3 3
  0 2
  3 1
  4 2
  0 1
  8 1
  4 4
  30 2
  30 12
  2 12
  2 2
  15 2
  30 8
  13 14
  2 8
  8 5
  13 5
  21 7
  21 9
  18 15
  11 15
  6 10
  6 8
  8 5
  10 12
  5 9
  15 6
  20 10
  18 12
  3 3
  5 5
  10 3
  10 10
  20 8
  10 15
  10 8
  4 4
  -98 99
  -99 -99
  99 -98
  99 97
  -99 99
  -98 -98
  99 -99
  96 99
  0 0
  

  Output for the Sample Input

  4.708333333333333
  1680.0000000000005
  491.1500000000007
  0.0
  7600258.4847715655

• 题解：朴素想法，求出公共部分的凸多面体的顶点坐标，然后再计算其体积。公共部分的凸多面体的顶点都是一个棱柱的侧面与另一个棱柱的侧棱的交点，可以通过O(nm)时间的枚举求得，但因为涉及三维空间的几何运算，实现起来是非常麻烦的。
  事实上，沿x轴对棱柱切片即可：按某个值对侧棱与z轴平行的棱柱P₁切片后，就得到了[y₁,y₂]*(-∞,∞)这样的在z轴方向无限延伸的长方形的横截面，同样的，我们按某个x值对侧棱与y轴平行的棱柱P₂切片后，就得到了(-∞,∞)*[z₁,z₂]这样的在y轴方向无限延伸的长方形的横截面。因此，我们按某个x值对两个棱柱的公共部分切片后，得到的横截面就是长方形[y₁,y₂]*[z₁,z₂]。而长方形的面积通过(y₂-y₁)*(z₂-z₁)就可以求得，关于x轴对面积求积分就能得到公共部分的体积了。
  首先，枚举出原棱柱底面顶点的所有x坐标并排序，在相邻两个x坐标之间的区间中按x值切片得到的长方形的顶点坐标是关于x的线性函数，所以面积就是关于x的二次函数，其积分很容易计算，虽然可以通过求得表达式后再来计算二次函数的积分，但应用Simpson公式则更为轻松。Simpson公式如下：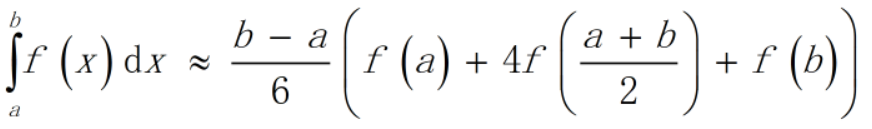
  

  Simpson公式就是在数值积分中用二次函数来近似原函数进行积分而得到的公式，如果原函数本身就是次数不超过二的多项式，那么用Simpson公式就可以得到精确的积分值。利用该公式，无需求出关于x的多项式，而只要计算按区间的端点和中点切片得到的长方形的面积就够了。

• 代码：

  #include<cstdio>
  #include<algorithm>
  #include<vector>
  
  using namespace std;
  
  const int INF=0x3f3f3f3f;
  const double EPS=1e-;
  const int MAX_N=;
  int N,M;
  int X1[MAX_N], Y1[MAX_N], X2[MAX_N], Z2[MAX_N];
  
  double max(double x, double y)
  {
      if (x>y+EPS) return x;
      return y;
  }
  
  double min(double x, double y)
  {
      if (x<y-EPS) return x;
      return y;
  }
  
  double width(int * X, int * Y, int n, double x)
  {
      double lb=INF, ub=-INF;
      for (int i=; i<n; i++)
      {
          double x1=X[i], y1=Y[i], x2=X[(i+)%n], y2=Y[(i+)%n];
          if ((x1-x)*(x2-x)<= && x1!=x2)
          {
              double y=y1+(y2-y1)*(x-x1)/(x2-x1);
              lb=min(lb, y);
              ub=max(ub, y);
          }
      }
      return max(0.0, ub-lb);
  }
  
  int main()
  {
      while (~scanf("%d %d", &M, &N))
      {
          if (M== && N==) break;
          for (int i=; i<M; i++)
          {
              scanf("%d %d", &X1[i], &Y1[i]);
          }
          for (int i=; i<N; i++)
          {
              scanf("%d %d", &X2[i], &Z2[i]);
          }
          int min1=*min_element(X1, X1+M), max1=*max_element(X1, X1+M);
          int min2=*min_element(X2, X2+N), max2=*max_element(X2, X2+N);
          vector<int> xs;
          for (int i=; i<M; i++) xs.push_back(X1[i]);
          for (int i=; i<N; i++) xs.push_back(X2[i]);
          sort(xs.begin(), xs.end());
          double res=;
          for (int i=; i+<xs.size(); i++)
          {
              double a=xs[i], b=xs[i+], c=(a+b)/;
              if (min1<=c && c<=max1 && min2<=c && c<=max2)
              {
                  double fa=width(X1, Y1, M, a)*width(X2, Z2, N, a);
                  double fb=width(X1, Y1, M, b)*width(X2, Z2, N, b);
                  double fc=width(X1, Y1, M, c)*width(X2, Z2, N, c);
                  res+=(b-a)/*(fa+*fc+fb);
              }
          }
          printf("%.10f\n", res);
      }
  }