Luogu 3376 【模板】网络最大流

0.网络流解释：如果你还是不能理解，我们就换一种说法，假设s城有inf个人想去t城，但是从s到t要经过一些城市才能到达，（以上图为例）其中s到3城的火车票还剩10张，3到t的火车票还剩15张，其他路以此类推，问最终最多能有多少人能到达t城？（假设这个地区只有火车，没有汽车飞机，步行和骑自行车会累死就不考虑了，再假设所有人都买得起火车票。）

1.https://www.cnblogs.com/zsboy/archive/2013/01/27/2878810.html EK 算法 ，但是“反悔”那个图应该9 1 9 1 9 。

2. Dinic算法可以每次找出多条增广路，为什么要分层呢？分层图是有向无环图。

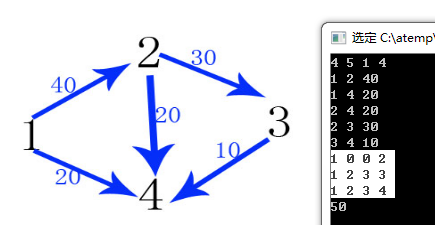
每bfs一次的结果在运行框中。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<queue>
#define inf 0x3f3f3f3f
using namespace std;
int hd[10005],cnt=-1,d[10005],vis[10005],cur[10005];
struct Edge{
    int to,vl,nxt;
}edge[200005];
void add(int u,int v,int w)
{
    cnt++;
    edge[cnt].to =v;
    edge[cnt].nxt=hd[u];
    edge[cnt].vl=w;
    hd[u]=cnt;
}
queue<int> q;
int s,t;
int bfs()
{
    memset(d,0,sizeof d);
    memset(vis,0,sizeof vis);
    while(q.size()) q.pop() ;//这个不写会T
    d[s]=1;vis[s]=1;
    q.push(s);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=hd[u];i!=-1;i=edge[i].nxt)//边是从零开始的，因此这里可以不能是i>0 //同一条边还有容量可以流怎么办，边已经遍历完
        {
            int v=edge[i].to;
            if(!vis[v] && edge[i].vl>0)
            {
                vis[v]=1;
                d[v]=d[u]+1;
                q.push(v);
                if(v==t)return 1;
            }
        }
    }
    return 0;
}

int dinic(int u,int res)//
{
    if(u==t) return res;
    int sum=0;
    for(int i=cur[u];i!=-1;i=edge[i].nxt)
    {
        cur[u]=i;//当前弧优化,不符合的通道就不再判断了
        int v=edge[i].to;
        if(d[u]+1==d[v] && edge[i].vl>0 && res>0)//
        {
            int k=dinic(v,min(res,edge[i].vl));    //剩余流量及该路径容量的最小值
            if(!k)
            {
                d[v]=0;//去掉增广完的点
                break;
            }
            edge[i].vl-=k;
            edge[i^1].vl+=k;
            res-=k;
            sum+=k;
        }
    }
    return sum;
}
int n,m,u,v,w,flow,mxflow;
int main()
{
    scanf("%d%d%d%d",&n,&m,&s,&t);
    memset(hd,-1,sizeof hd);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);
        add(v,u,0);
    }
//    for(int i=1;i<=n;i++)
//        cout<<d[i]<<" ";
//    cout<<endl;
    while(bfs()){
        while(flow=dinic(s,inf))
            mxflow+=flow;
    }
    cout<<mxflow<<endl;
}