（新手向）N皇后问题详解（DFS算法）

非常经典的一道题：

N皇后问题： 
国际象棋中皇后的势力范围覆盖其所在的行、列以及两条对角线，现在考察如下问题：如何在n x n的棋盘上放置n个皇后，使得她们彼此互不攻击 。

免去麻烦我们这里假定n不是很大。。。

（图片来自百度百科（这是8皇后问题的一种解法））

某leetcode大犇曾说过：“这个问题和解数独题目有一个很大的共同点，那就是：我都不会。”

好了下面开始分析：（废话警告）

初步判断这问题的特点有：

1.有个场地来放置单位。

2.各个单位之间有制约。

3.没有特殊的数学方法，得把某一个摆法摆出来才能判断是否可行。

于是萌新一般都会这么想：对于1,：我搞个二维数组来存。对于2：我搞个判定函数来一个一个判定。对于3：我暴力枚举。

那么算法框架大概就是：我对二维数组的所有情况进行枚举，然后对每种情况进行判定

over ，输个数字n，按下回车，双手离开键盘，等了老半天发现命令提示符只有个光标在跳动 |

如果是在做网题，说不定就判定是超时或者内存溢出，过不了。

然后就开始思考怎么优化：

对于1，我可以缩减吗····，改成一维数组，，，似乎徒增麻烦。

对于2，我可以有更巧妙的判断方法吗？·············有个鬼，还不得把每个棋子的每一行每一列每两个斜线都瞅一下。

对于3，我一定要把所有情况都举出来嘛？···(于是脑子里面开始摆起了棋子,模拟算法过程)

然后就会发现  比如第一行前两个格子一开始就摆了两个相邻的棋子，诶这不明摆着皇后互怼了吗！后面还继续枚举就太傻了吧···

　　　　　这种傻事情做了不是白白增加耗时吗！

　　　　　　所以就思考如何在这种“傻情况”出现的时候就pass掉后面所有情况。。。

于是脑子陷入了一团乱麻。。。

打住！

咱们换个思考方式，既然直接想有点困难，不如我们想办法先做点处理，让这些玩意儿便于我们把弄。

再回头想想规则，皇后可以吃掉所处的一行一列以及斜线上的棋子，那也就是说，每一行都最多只能有一个棋子，每一列都最多只能有一个棋子，

那我们不妨把每一行看成一组！

那么这一组就只有n个可能性（一行n个位置 每一次只有一个位置被占用）

也就是单个一行有n种可能性

因为有n行

哈哈那么就瞬间只需要讨论n*n种可能性了！

还记得我们之前的思考吗？：

对于3，我一定要把所有情况都举出来嘛？···(于是脑子里面开始摆起了棋子,模拟算法过程)

     然后就会发现  比如第一行前两个格子一开始就摆了两个相邻的棋子，诶这不明摆着皇后互怼了吗！后面还继续枚举就太傻了吧···

　　　这种傻事情做了不是白白增加耗时吗！

　　　所以就思考如何在这种“傻情况”出现的时候就pass掉后面所有情况。。。

像这种情况：

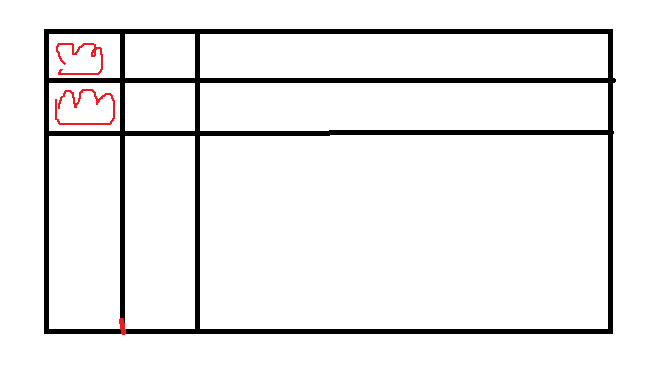（我的天这皇后画的...）

显然下面3,4,5····行都不用枚举了，直接pass掉

于是我们思路慢慢清晰了起来：

我们从第一行开始枚举，第一行第一格：

然后枚举第二行，也从第一格开始：

判定一下，哇，不行，咋办呢？这情况下面所有行都没有枚举的必要了，但是本行还是可以继续的。。。于是我们开始枚举第二行第二个情况：

不行（斜线上互吃）。

继续第二行下一个情况：

行嘞！

那么我们就可以开第三行了：

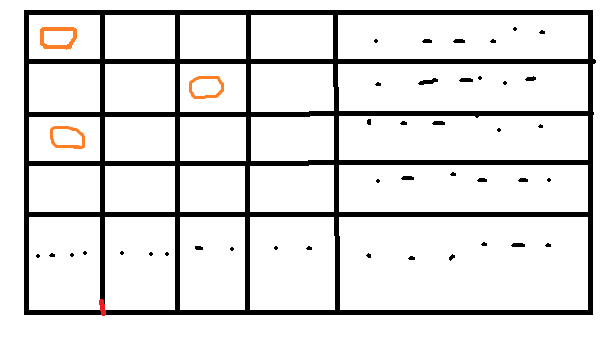
不行（一列上吃）。

不行（斜线上吃）

不行。

还不行

行嘞！

··················

好了，算法思路大概就出来了。

我们就这样干下去，直到最后一行可行，那么我们就获得了一个可行解了，

然后我们想继续获得其他解，那么继续枚举下去，但是要退一步：

先从倒数第一行开始，我们枚举下一个，有解则输出，无解则继续。

倒数第一行结束了，咋办？

别忘了倒数第二行的情况还不一定枚举完了呢。

于是退到倒数第二行，继续如上操作。

··················

---

干说着没用，撸代码：

#include<iostream>

using namespace std;
int main()
{
    return ;
}

先准备好需要用的存储（这里用64个绰绰有余）

ans是用来存每一次的解 ans[1]表示第一行的那个元素的所在列的位置

 #include<iostream>

 using namespace std;
 bool colMark[] = {  };//元素所在列  如果有了元素在第k列 那么colMark[k]就标记上true
 bool naMark[] = {  };//捺，撇···顾名思义，表示元素所在的两个斜线o.o 原理同上
 bool pieMark[] = {  };
 int total = ;           //解的总个数
 int N = ;
 int ans[] = {  };
 int main()
 {
     return ;
 }

然后下面先写一个显示函数：

 void showOneSolution()//用来显示一个解
 {
     total++;
     for (int i = ; i<=N; ++i)
     {
         cout << ans[i] << " ";
     }
         cout << endl;
 }

下面是核心：

void Dfs(int i)   //可以百度学习 深度优先搜索
{
    if (i > N)              //判断是否已经枚举完了N行
    {
        showOneSolution();  //枚举完了就输出（此刻我们处于N+1行）
        return;             //返回到第N行
    }
    for (int j = ; j <= N; ++j) //这里的j表示  本行的第j列
    {
        if ((!colMark[j])&&(!naMark[j-i+N])&&(!pieMark[i+j]))    //这里的"j-i+N"  "i+j"建议自己体会
        {　　　　　　　　　　//判断这个格子所在的两个斜线和所在列是否为空
            colMark[j] = true;
            naMark[j - i + N] = true;
            pieMark[i + j] = true;
            ans[i] = j;
            Dfs(i + );
            colMark[j] = false;      //这个格子枚举完了要进入本行第j+1个格子（或者结束本行） 走之前别忘了恢复标记
            naMark[j - i + N] = false;
            pieMark[i + j] = false;
        }
    }
}

最后组装起来：（当然啦，还是建议自己撸代码，你会发现很多意想不到的问题~解决问题的同时也是进步）

 #include<iostream>

 using namespace std;
 bool colMark[] = {  };
 bool naMark[] = {  };
 bool pieMark[] = {  };
 int total = ;
 int N = ;
 int ans[] = {  };
 void showOneSolution()//用来显示一个解
 {
     total++;
     for (int i = ; i<=N; ++i)
     {
         cout << ans[i] << " ";
     }
         cout << endl;
 }
 void Dfs(int i)
 {
     if (i > N)              //判断是否已经枚举完了N行
     {
         showOneSolution();  //枚举完了就输出（此刻我们处于N+1行）
         return;             //返回到第N行
     }
     for (int j = ; j <= N; ++j) //这里的j表示  本行的第j列
     {
         if ((!colMark[j]) && (!naMark[j - i + N]) && (!pieMark[i + j]))
         {　　　　　　　　　　//判断这个格子所在的两个斜线和所在列是否为空
             colMark[j] = true;
             naMark[j - i + N] = true;
             pieMark[i + j] = true;
             ans[i] = j;
             Dfs(i + );
             colMark[j] = false;      // 走之前别忘了恢复标记
             naMark[j - i + N] = false;
             pieMark[i + j] = false;
         }
     }
 }
 int main()
 {
     cin >> N;
     Dfs();
     cout << total;
     system("pause");
     return ;
 }

---

总结：

思路混乱不妨换个角度理一理。

在纸上面画一画算法过程会有不少帮助。

代码少出错还是得多撸。

想什么呢？！撸代码！