Andrew Ng机器学习课程笔记（二）之逻辑回归

Andrew Ng机器学习课程笔记（二）之逻辑回归

版权声明：本文为博主原创文章，转载请指明转载地址

http://www.cnblogs.com/fydeblog/p/7364636.html

前言

学习了Andrew Ng课程，开始写了一些笔记，现在写完第5章了，先把这5章的内容放在博客中，后面的内容会陆续更新！

这篇博客主要记录了Andrew Ng课程第二章逻辑回归，主要介绍了梯度下降法，逻辑回归的损失函数，多类别分类等等

简要介绍：逻辑回归算法是分类算法，我们将它作为分类算法使用。有时候可能因为这个算法的名字中出现了回归”使你感到困惑，但逻辑回归算法实际上是一种分类算法，它适用于标签 y 取值离散的情况，如：1 0 0 1。比如对邮件进行分类，垃圾邮件用表示，非垃圾邮件用0表示。

实现算法：梯度下降算法

1. 建立逻辑回归假设

括号内的 x跟线性回归的一样，主要是套上g(x)，压缩它的函数值范围，方便分类判决。

g(x)的表达式如下：

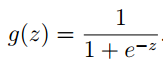
根据这个函数特性，我们可以知道，g(z)的范围是在（0,1），函数图形如下：

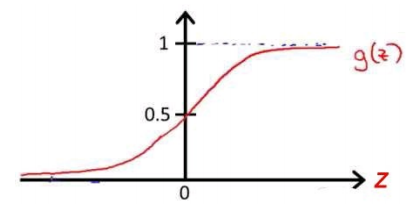
当hθ大于等于0.5时，预测 y=1；当hθ小于 0.5 时，预测 y=0。

2.建立代价函数

对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数（ non-convex function）

如下图所示

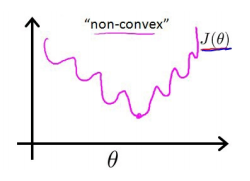
这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。所以需要定义新的代价函数

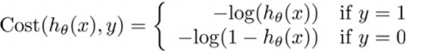
hθ(x)与 Cost(hθ(x),y)之间的关系如下图所示：

这样构建的Cost(hθ(x),y)函数的特点是： 当实际的y=1且hθ也为1时误差为0，当y=1但hθ不为1时误差随着 hθ的变小而变大；当实际的
y=0 且hθ也为 0 时代价为
0，当 y=0 但 hθ不为0时误差随着 hθ的变大而变大。这样符合单调性，就可以使用梯度下降法。

于是代价函数定义如下

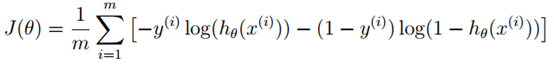
3. 参数更新迭代

这个与线性回归相同

4. 多类别分类： 一对多

很多时候，我们分类的数目是多个的，这里介绍一个叫做"一对多" (one-vs-all) 的分类算法。

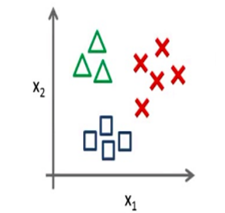
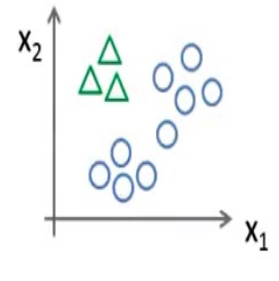
我们将多个类中的一个类标记为正向类（y=1），然后将其他所有类都标记为负向类，如图

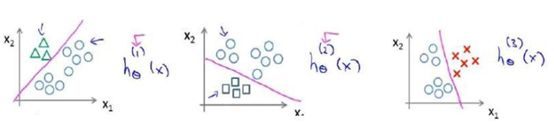
在我们需要做预测时，我们将所有的分类机都运行一遍，然后对每一个输入变量，都选择最高可能性的输出变量。（就是比较图中三个hθ(x)，找到最大值，并判断为相应的类型）