[Noi2014]购票 BZOJ3672 点分治+斜率优化+CDQ分治

Description

 今年夏天，NOI在SZ市迎来了她30周岁的生日。来自全国 n 个城市的OIer们都会从各地出发，到SZ市参加这次盛会。全国的城市构成了一棵以SZ市为根的有根树，每个城市与它的父亲用道路连接。为了方便起见，我们将全国的 n 个城市用 1 到 n 的整数编号。其中SZ市的编号为 1。对于除SZ市之外的任意一个城市 v，我们给出了它在这棵树上的父亲城市 f_v  以及到父亲城市道路的长度 s_v。从城市 v 前往SZ市的方法为：选择城市 v 的一个祖先 a，支付购票的费用，乘坐交通工具到达 a。再选择城市 a 的一个祖先 b，支付费用并到达 b。以此类推，直至到达SZ市。对于任意一个城市 v，我们会给出一个交通工具的距离限制 l_v。对于城市 v 的祖先 a，只有当它们之间所有道路的总长度不超过 l_v 时，从城市 v 才可以通过一次购票到达城市 a，否则不能通过一次购票到达。对于每个城市 v，我们还会给出两个非负整数 p_v,q_v  作为票价参数。若城市 v 到城市 a 所有道路的总长度为 d，那么从城市 v 到城市 a 购买的票价为 dp_v+q_v。每个城市的OIer都希望自己到达SZ市时，用于购票的总资金最少。你的任务就是，告诉每个城市的OIer他们所花的最少资金是多少。

Input

第 1 行包含2个非负整数 n,t，分别表示城市的个数和数据类型（其意义将在后面提到）。输入文件的第 2 到 n 行，每行描述一个除SZ之外的城市。其中第 v 行包含 5 个非负整数 f_v,s_v,p_v,q_v,l_v，分别表示城市 v 的父亲城市，它到父亲城市道路的长度，票价的两个参数和距离限制。请注意：输入不包含编号为 1 的SZ市，第 2 行到第 n 行分别描述的是城市 2 到城市 n。

Output

输出包含 n-1 行，每行包含一个整数。其中第 v 行表示从城市 v+1 出发，到达SZ市最少的购票费用。同样请注意：输出不包含编号为 1 的SZ市。

Sample Input

7 3
1 2 20 0 3
1 5 10 100 5
2 4 10 10 10
2 9 1 100 10
3 5 20 100 10
4 4 20 0 10

Sample Output

40
150
70
149
300
150

 

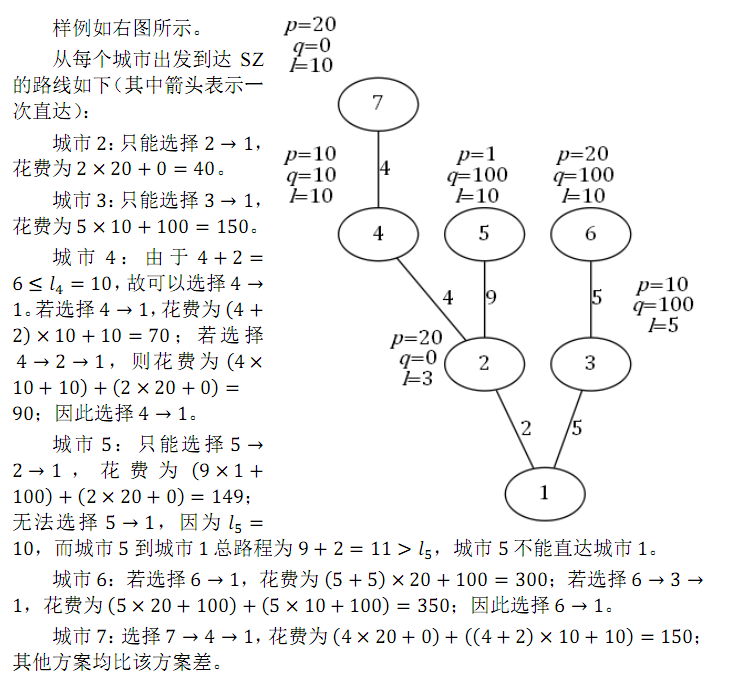
对于所有测试数据，保证 0≤p_v≤10⁶，0≤q_v≤10¹²，1≤f_v<v；保证 0<s_v≤l_v≤2×10¹¹，且任意城市到SZ市的总路程长度不超过 2×10¹¹。

输入的 t 表示数据类型，0≤t<4，其中：

当 t=0 或 2 时，对输入的所有城市 v，都有 f_v=v-1，即所有城市构成一个以SZ市为终点的链；

当 t=0 或 1 时，对输入的所有城市 v，都有 l_v=2×10¹¹，即没有移动的距离限制，每个城市都能到达它的所有祖先；

当 t=3 时，数据没有特殊性质。

n=2×10^5

分析：

先考虑一下暴力...其实前3个点的分还是很好拿的...稍微搞一搞就出来了，n^2DP比较显然...

后面的呢，应该拿50分没有什么大问题的说...一条链的斜率优化实在不能再好写一点了...

附上30分的暴力：

#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
#include <queue>
#include <cstdlib>
using namespace std;
#define N 200005
#define ll long long
struct node{int to,next;}e[N<<1];
int fa[N],n,head[N],cnt;
ll f[N],dep[N],l[N],p[N],q[N],a[N];
void add(int x,int y){e[cnt]=(node){y,head[x]};head[x]=cnt++;}
void dfs(int x,int from)
{
    fa[x]=from;dep[x]=dep[from]+a[x];
    for(int t=fa[x];t&&dep[x]-dep[t]<=l[x];t=fa[t])f[x]=min(f[t]+(dep[x]-dep[t])*p[x]+q[x],f[x]);
    for(int i=head[x];i!=-1;i=e[i].next)if(e[i].to!=from)dfs(e[i].to,x);
}
int main()
{
    scanf("%d%*d",&n);memset(head,-1,sizeof(head));memset(f,0x3f,sizeof(f));
    for(int i=2;i<=n;i++)
    {
        scanf("%d%lld%lld%lld%lld",&fa[i],&a[i],&p[i],&q[i],&l[i]);
        add(fa[i],i);add(i,fa[i]);
    }f[1]=0;dfs(1,0);
    for(int i=2;i<=n;i++)printf("%lld\n",f[i]);return 0;
}

目测我似乎能跑过4个点...反正就是这个样子的暴力...

f[x]=max{f[j]+(dep[x]-dep[j])*p[x]+q[x]};（j是x的祖先，满足dep[x]-dep[j]<=l[x]）

显然...发现dep单调，p[x]不单调，但这不是问题用不着写什么奇怪的东西，每次二分导函数即可...

但是，这个题出在树上就让人很崩溃了...显然，我们考虑有两种斜率优化的方法可以选择。

(1)动态维护凸包+二分查找 → 如果你会可持久化凸包的话可以考虑考虑，至于树剖+动态凸包能不能过...反正时间复杂度有问题...nlog^3n实在是不忍直视...

(2)CDQ分治（前置技能：货币兑换）每次考虑如何维护凸包用来更新节点，那么考虑选择一个链更新一个点的子树，那么这样的话，只需要维护一个凸包就可以了。这种情况下，满足直接二分转移一下就可以了。那么如何选择这个点，显然，我们可以选择树的重心，因为这样的话，满足子树的最大一个小于n/2，转移次数<=logn（点分治），每次遍历满，时间复杂度O(nlog^2n)。

可以考虑，如果一个点，满足所有的父亲节点都被确定，那么这个点就可以被确定，并且可以用这条链更新这个点的子树，那么我们每次找到重心之后，先找到它的父节点那部分作为CDQ分治的左部分，用左部分更新重心的子树并将其更新，之后再递归处理其他的子部分。而每次可以发现，我们dep是单调递增的，维护一个凸包，之后按照子树中节点能够更新的最深的位置进行排名，每次进行二分导函数，找到最优解（同任务安排），其实也就是把树分治当做CDQ分治来做。

附上代码：

#include <cstdio>
#include <cmath>
#include <iostream>
#include <queue>
#include <algorithm>
#include <cstring>
#include <cstdlib>
#include <bitset>
using namespace std;
#define N 200005
#define ll long long
#define K(x) (-dep[x])
#define B(x) (f[x])
#define Y(x,y) (K(x)*p[y]+B(x))
struct egde{int to,next;}e[N<<1];
int head[N],cnt,fa[N],siz[N],sn,rot,mx[N],vis[N],q[N],lx[N],ln,n,rx[N],rn,tail;
ll dep[N],p[N],l[N],f[N],b[N];
void add(int x,int y){e[cnt]=(egde){y,head[x]};head[x]=cnt++;}
void get_root(int x,int from)
{
	siz[x]=1,mx[x]=0;
	for(int i=head[x];i!=-1;i=e[i].next)
	{
		int to1=e[i].to;
		if(to1!=from&&!vis[to1])
		{
			get_root(to1,x);
			siz[x]+=siz[to1];
			mx[x]=max(siz[to1],mx[x]);
		}
	}
	mx[x]=max(mx[x],sn-siz[x]);
	if(mx[x]<mx[rot])rot=x;
}
bool cmp(int i,int j,int k)
{
	long double t1=(long double)(K(k)-K(i))*(B(k)-B(j));
	long double t2=(long double)(K(k)-K(j))*(B(k)-B(i));
	return t1>=t2-1e-10;
}
bool cmp1(const int &a,const int &b){return dep[a]-l[a]>dep[b]-l[b];}
void get_rx(int x,int from)
{
	if(from!=0)rx[++rn]=x;
	for(int i=head[x];i!=-1;i=e[i].next)
	{
		int to1=e[i].to;
		if(to1!=from&&!vis[to1])get_rx(to1,x);
	}
}
void Update(int x)
{
	if(!tail)return ;int l=1,r=tail;
	while(l<r)
	{
		int m=(l+r)>>1;
		if(Y(q[m],x)>Y(q[m+1],x))l=m+1;
		else r=m;
	}
	f[x]=min(f[x],Y(q[l],x)+b[x]);
}
void dfs(int x)
{
	int rt;
	sn=siz[x],rot=0,get_root(x,0),rt=rot,vis[rt]=1;
	// printf("%d %d\n",x,rt);
	if(x!=rt)siz[x]-=siz[rt],dfs(x);
	tail=ln=rn=0;lx[++ln]=rt;
	for(int i=rt;i!=x;i=fa[i])
	{
		if(dep[rt]-l[rt]<=dep[fa[i]])f[rt]=min(f[rt],Y(fa[i],rt)+b[rt]);
		lx[++ln]=fa[i];
	}
	get_rx(rt,0);sort(rx+1,rx+rn+1,cmp1);
	// if(x==1)for(int i=1;i<=rn;i++)printf("%d %d\n",rt,rx[i]);
	int j=1;
	for(int i=1;i<=ln&&j<=rn;i++)
	{
		while(j<=rn&&dep[lx[i]]<dep[rx[j]]-l[rx[j]])Update(rx[j++]);
		while(tail>1&&cmp(q[tail],q[tail-1],lx[i]))tail--;
		q[++tail]=lx[i];
	}while(j<=rn)Update(rx[j++]);
	for(int i=head[rt];i!=-1;i=e[i].next)
	{
		int to1=e[i].to;
		if(!vis[to1])dfs(to1);
	}
}
int main()
{
	scanf("%d%*d",&n);memset(f,0x3f,sizeof(f));memset(head,-1,sizeof(head));
	for(int i=2;i<=n;i++)
	{
		scanf("%d%lld%lld%lld%lld",&fa[i],&dep[i],&p[i],&b[i],&l[i]);
		dep[i]+=dep[fa[i]];b[i]+=dep[i]*p[i];add(fa[i],i);add(i,fa[i]);
		// printf("%d\n",b[i]);
	}f[1]=0;mx[0]=1<<30,siz[1]=n;dfs(1);
	for(int i=2;i<=n;i++)printf("%lld\n",f[i]);return 0;
}