bzoj3336 Uva10572 Black and White

题目描述：

数据范围：2<=n,m<=8

题解：

很明显需要状压。但是怎么压不知道，压什么不知道。

然后从条件下手。

条件1要求黑色在一起白色在一起，记录轮廓线很容易做到。

条件2要求不能出现$2*2$的同色方格。我们还需要再记录当前位置的左上角。

所以这道题的轮廓线长这样。

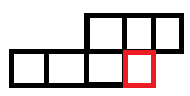
丑图。

我们需要确定一个顺序记录哪几块互相联通。由于轮廓线奇特的形状我决定这样标号。

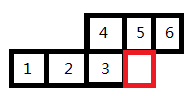
如果编号相同但是并不互相联通我们可以知道他俩不同颜色。

为了颜色我们决定记录某个块的颜色，这样可以得到所有颜色。

于是这道题表中存的就是$1$号颜色+所有状态。

为了方便调试我用了十进制。

每次调用时都要解压，处理后压缩放回去。

由于第一行和第一列找不到长这样的轮廓线，我们可以搜出第一行所有状态，处理第一列时直接枚举黑色/白色。

接下来就是精彩的特判环节。

（这一部分针对处于中心部位的一干普通点）

以填黑色为例。

如果这里不能填黑：

1.输入要求白色。

2.拐角处已经有三个黑块。

3.要考虑到上图中红块填上后$5$号块就不再与不定颜色相邻，我们不能把$5$号块憋死我们要判断$5$号是否有与之联通的好朋友在轮廓线上。

类似围棋中的气。

如果没有而且$5$号是白的，那么就不能填黑！

等等好像是错的。

如果红块已经到$(n,m-1)$或者是$(n,m)$，而且轮廓线上其他都是黑的，我们可以放黑色。

所以这又是个特判。

4.对于3我们考虑的是上下断开，能否出现左右断开？

当然可能。

但是只能在最后一行出现。

所以统计答案时要填回去看一眼。

真 恶心。

深思熟虑后糊上去的代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 15
#define ll long long
int T,n,m,k,a[N][N];
char ch[N][N];
ll bas[N],ans;
struct Map
{
    int hed[],cnt[];
    struct EG
    {
        int nxt;
        ll to,w;
    }e[2][];
    void ae(int f,ll t,ll w)
    {
        e[++cnt[k]][k].to = t;
        e[cnt[k]][k].nxt = hed[f];
        e[cnt[k]][k].w = w;
        hed[f] = cnt[k];
    }
    void push(ll u,ll w)
    {
        for(int j=hed[u%];j;j=e[j][k].nxt)
            if(e[j][k].to==u)
            {
                e[j][k].w += w;
                return ;
            }
        ae(u%,u,w);
    }
    void clear()
    {
        cnt[k] = ;
        memset(hed,,sizeof(hed));
    }
}mp;
int col[N],grp[N],tmp[N],las[N];
ll zip()
{
    ll ret = ;
    for(int i=;i<=m+;i++)ret=*(ret+grp[i]);
    return ret+col[];
}
void upz(ll u)
{
    memset(tmp,-,sizeof(tmp));
    tmp[]=u%;u/=;
    for(int i=m+;i>=;i--,u/=)grp[i]=u%;
    for(int i=;i<=m+;i++)
        if(tmp[grp[i]]==-)tmp[grp[i]]=tmp[grp[i-]]^;
    for(int i=;i<=m+;i++)
        col[i]=tmp[grp[i]];
}
void shake()//get the express
{
    memset(tmp,,sizeof(tmp));
    for(int cnt=,i=;i<=m+;i++)
        if(!tmp[grp[i]])tmp[grp[i]]=++cnt;
    for(int i=;i<=m+;i++)grp[i]=tmp[grp[i]];
}
bool find_friend(int now,int beg,int ens)
{
    int cnt = ;
    for(int i=beg;i<=ens;i++)
        if(grp[i]==now)cnt++;
    return cnt>;
}
bool ck1()
{
    for(int i=;i<=m;i++)
        if(col[i]+a[][i]==)return ;
    return ;
}
bool ck2()
{
    int cnt = ;
    for(int i=;i<=m;i++)
        cnt+=(col[i]!=col[i-]);
    return cnt<=;
}
int ck3(int c)
{
    if(col[m-]==col[m]&&col[m]==col[m+]&&col[m+]==c)return ;
    int c0 = col[m],ret=;
    for(int i=;i<=m+;i++)las[i]=grp[i];
    col[m] = c;grp[m] = m+;
    if(col[m-]==c)
    {
        int kg = grp[m-];
        for(int i=;i<=m+;i++)if(grp[i]==kg)grp[i]=m+;
    }
    if(col[m+]==c)
    {
        int kg = grp[m+];
        for(int i=;i<=m+;i++)if(grp[i]==kg)grp[i]=m+;
    }
    shake();
    for(int i=;i<=m+;i++)if(grp[i]>)ret = ;
    for(int i=;i<=m+;i++)grp[i] = las[i];
    if(col[m-]==c)
    {
        int kg = grp[m-];
        for(int i=;i<=m+;i++)if(grp[i]==kg)grp[i]=m+;
    }
    if(col[m+]==c)
    {
        int kg = grp[m+];
        for(int i=;i<=m+;i++)if(grp[i]==kg)grp[i]=m+;
    }
    shake();
    for(int i=;i<=m+;i++)if(grp[i]>)ret = ;
    for(int i=;i<=m+;i++)grp[i]=las[i];
    col[m] = c0;
    return ret;
}
void PushF()
{
    for(int i=;i<(<<m);i++)
    {
        for(int j=;j<=m;j++)col[j]=(i>>(j-))&;
        if(!ck1())continue;
        if(!ck2())continue;
        grp[]=;
        for(int j=;j<=m+;j++)if(col[j]==col[j-])grp[j]=grp[j-];else grp[j]=grp[j-]+;
        mp.push(zip(),);
    }
}
bool check_b(int i,int j)
{
    if(a[i][j]==)return ;
    if(col[j-]==&&col[j]==&&col[j+]==)return ;
    if((i!=n||j!=m)&&(i!=n||j!=m-))
        if(col[j+]==&&!find_friend(grp[j+],j+,m+)&&!find_friend(grp[j+],,j-))
            return ;
    return ;
}
bool check_w(int i,int j)
{
    if(a[i][j]==)return ;
    if(col[j-]==&&col[j]==&&col[j+]==)return ;
    if((i!=n||j!=m)&&(i!=n||j!=m-))
        if(col[j+]==&&!find_friend(grp[j+],j+,m+)&&!find_friend(grp[j+],,j-))
            return ;
    return ;
}
int main()
{
//    freopen("tt.in","r",stdin);
    scanf("%d",&T);
    bas[]=;
    for(int i=;i<=;i++)bas[i] = *bas[i-];
    while(T--)
    {
        scanf("%d%d",&n,&m);
        for(int i=;i<=n;i++)
        {
            scanf("%s",ch[i]+);
            for(int j=;j<=m;j++)
            {
                if(ch[i][j]=='o')a[i][j]=;
                else if(ch[i][j]=='#')a[i][j]=;
                else a[i][j]=;
            }
        }
        ans=,k=,mp.clear();
        PushF();
        for(int i=;i<=n;i++)
        {
            k^=;mp.clear();
            for(int j=;j<=mp.cnt[!k];j++)
            {
                ll now = mp.e[j][!k].to,val = mp.e[j][!k].w;
                upz(now);
                for(int o=m+;o>=;o--)grp[o]=grp[o-],col[o]=col[o-];
                for(int q=;q<=m+;q++)las[q]=grp[q];
                if(a[i][]!=)//black
                {
                    if(col[]==)
                    {
                        col[]=,grp[]=grp[];
                        shake();
                        mp.push(zip(),val);
                    }else
                    {
                        if(find_friend(grp[],,m+))
                        {
                            col[]=,grp[]=m+;
                            shake();
                            mp.push(zip(),val);
                        }else if(i==n&&m==)
                        {
                            col[]=,grp[]=m+;
                            shake();
                            mp.push(zip(),val);
                        }
                    }
                }
                for(int q=;q<=m+;q++)grp[q]=las[q];
                if(a[i][]!=)//white
                {
                    if(col[]==)
                    {
                        col[]=,grp[]=grp[];
                        shake();
                        mp.push(zip(),val);
                    }else
                    {
                        if(find_friend(grp[],,m+))
                        {
                            col[]=,grp[]=m+;
                            shake();
                            mp.push(zip(),val);
                        }else if(i==n&&m==)
                        {
                            col[]=,grp[]=m+;
                            shake();
                            mp.push(zip(),val);
                        }
                    }
                }
            }
            for(int j=;j<=m;j++)
            {
                k^=,mp.clear();
                for(int o=;o<=mp.cnt[!k];o++)
                {
                    ll now = mp.e[o][!k].to,val = mp.e[o][!k].w;
                    upz(now);int c0 = col[j];
                    if(i==n&&j==m)
                    {
                        if(n==&&m==)
                        {
                            if(col[]==col[])
                            {
                                if((a[n][m]==||a[n][m]!=col[])&&col[]==col[])
                                    ans+=val*ck3(col[]^);
                                else if((a[n][m]==||a[n][m]==col[])&&col[]!=col[])
                                    ans+=val*ck3(col[]);
                            }else
                            {
                                if(a[n][m]==)ans+=val*(ck3()+ck3());
                                else ans+=val*ck3(a[n][m]);
                            }
                        }else
                        {
                            if(col[m-]==col[m+])
                            {
                                if(a[n][m]==||a[n][m]==col[m-])
                                    ans+=val*ck3(col[m-]);
                            }else
                            {
                                if(a[n][m]==)ans+=val*(ck3()+ck3());
                                else ans+=val*ck3(a[n][m]);
                            }
                        }
                        continue;
                    }
                    if(check_b(i,j))//black
                    {
                        col[j]=;grp[j]=m+;
                        for(int q=;q<=m+;q++)las[q]=grp[q];
                        if(col[j-]==)
                        {
                            int kg = grp[j-];
                            for(int q=;q<=m+;q++)if(grp[q]==kg)grp[q]=m+;
                        }
                        if(col[j+]==)
                        {
                            int kg = grp[j+];
                            for(int q=;q<=m+;q++)if(grp[q]==kg)grp[q]=m+;
                        }
                        shake();
                        if(i==n&&j==m)ans+=val;
                        mp.push(zip(),val);
                        for(int q=;q<=m+;q++)grp[q]=las[q];
                    }
                    col[j] = c0;
                    if(check_w(i,j))//white
                    {
                        col[j]=;grp[j]=m+;
                        if(col[j-]==)
                        {
                            int kg = grp[j-];
                            for(int q=;q<=m+;q++)if(grp[q]==kg)grp[q]=m+;
                        }
                        if(col[j+]==)
                        {
                            int kg = grp[j+];
                            for(int q=;q<=m+;q++)if(grp[q]==kg)grp[q]=m+;
                        }
                        shake();
                        if(i==n&&j==m)ans+=val;
                        mp.push(zip(),val);
                    }
                }
            }
        }
        printf("%lld\n",ans);
    }
    return ;
}