SVG可伸缩矢量图形
SVG可伸缩矢量图形
总结
1、svg就像普通标签那么使用
2、svg是xml
3、svg是矢量图,而canvas是位图
学习要点
- 对HTML5中的SVG有初步的了解
什么是SVG
简单的说SVG文档就是一些可以被直接嵌入到页面中的XML文档;
- SVG 指可伸缩矢量图形 (Scalable Vector Graphics)
- SVG 用于定义用于网络的基于矢量的图形
- SVG 使用 XML 格式定义图形
- SVG 图像在放大或改变尺寸的情况下其图形质量不会有损失
- SVG 是万维网联盟的标准
SVG 与 Canvas两者间的区别
- SVG 是一种使用 XML 描述 2D 图形的语言,Canvas 通过 JavaScript 来绘制 2D 图形。
- SVG 基于 XML,这意味着 SVG DOM 中的每个元素都是可用的。您可以为某个元素附加 JavaScript 事件处理器。
- 在 SVG 中,每个被绘制的图形均被视为对象。如果 SVG 对象的属性发生变化,那么浏览器能够自动重现图形。
- Canvas 是逐像素进行渲染的。在 canvas 中,一旦图形被绘制完成,它就不会继续得到浏览器的关注。如果其位置发生变化,那么整个场景也需要重新绘制,包括任何或许已被图形覆盖的对象。
实例
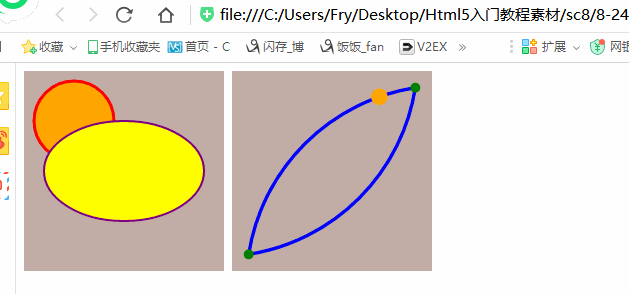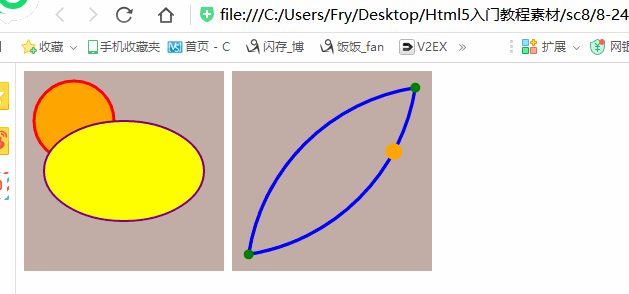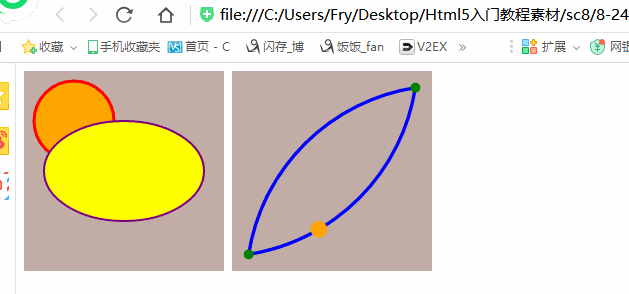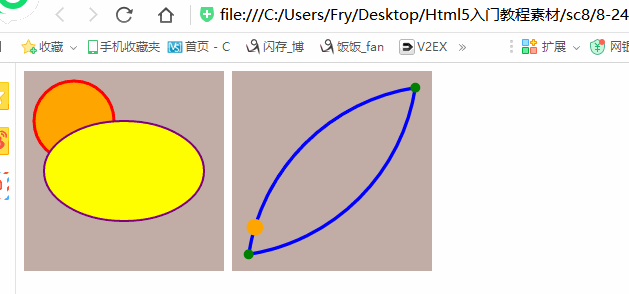
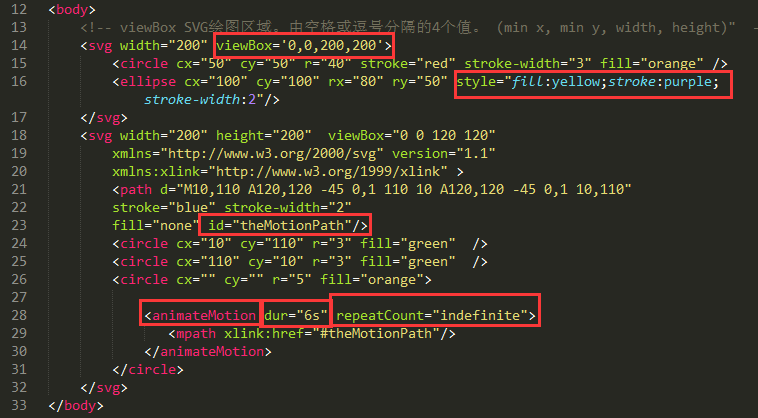
<!DOCTYPE html>
<html lang="zh-cn">
<head>
<meta charset="UTF-8">
<title>8-23 课堂演示</title>
<style type="text/css">
svg{
background: rgba(100,50,30,0.4);
}
</style>
</head>
<body>
<!-- viewBox SVG绘图区域。由空格或逗号分隔的4个值。 (min x, min y, width, height)" -->
<svg width="200" viewBox='0,0,200,200'>
<circle cx="50" cy="50" r="40" stroke="red" stroke-width="3" fill="orange" />
<ellipse cx="100" cy="100" rx="80" ry="50" style="fill:yellow;stroke:purple;stroke-width:2"/>
</svg>
<svg width="200" height="200" viewBox="0 0 120 120"
xmlns="http://www.w3.org/2000/svg" version="1.1"
xmlns:xlink="http://www.w3.org/1999/xlink" >
<path d="M10,110 A120,120 -45 0,1 110 10 A120,120 -45 0,1 10,110"
stroke="blue" stroke-width="2"
fill="none" id="theMotionPath"/>
<circle cx="10" cy="110" r="3" fill="green" />
<circle cx="110" cy="10" r="3" fill="green" />
<circle cx="" cy="" r="5" fill="orange"> <animateMotion dur="6s" repeatCount="indefinite">
<mpath xlink:href="#theMotionPath"/>
</animateMotion>
</circle>
</svg>
</body>
</html>
SVG可伸缩矢量图形的更多相关文章
- SVG 可伸缩矢量图形 简介 Path路径
w3school:http://www.w3school.com.cn/svg/svg_intro.asp SVG 意为可缩放矢量图形(Scalable Vector Graphics). SVG ...
- HTML5——添加新元素 新元素 Canvas SVG MathML 黑客帝国特效
为HTML添加新元素 添加新元素 + 该元素定义样式 <!DOCTYPE html> <html> <head> <meta charset=&quo ...
- D3js初探及数据可视化案例设计实战
摘要:本文以本人目前所做项目为基础,从设计的角度探讨数据可视化的设计的方法.过程和结果,起抛砖引玉之效.在技术方案上,我们采用通用web架构和d3js作为主要技术手段:考虑到项目需求,这里所做的可视化 ...
- Android群英传笔记——第七章:Android动画机制和使用技巧
Android群英传笔记--第七章:Android动画机制和使用技巧 想来,最 近忙的不可开交,都把看书给冷落了,还有好几本没有看完呢,速度得加快了 今天看了第七章,Android动画效果一直是人家中 ...
- 《响应式Web设计实践》学习笔记
原书: 响应式Web设计实践 目录: 第2章 流动布局 1. 布局选项 2. 字体大小 3. 网格布局 4. 混合固定宽度和流动宽度 第3章 媒介查询 1. 视口 2. 媒介查询结构 3. 内嵌样式与 ...
- 雷林鹏分享:XML 相关技术
XML 相关技术 下面是一个 XML 技术的列表. XHTML (可扩展 HTML) 更严格更纯净的基于 XML 的 HTML 版本. XML DOM (XML 文档对象模型) 访问和操作 XML 的 ...
- HTML+CSS知识总结2
一.position:absolute和float属性的异同 相同点:两者都可以让元素脱离文档流,并可设置宽高 不同点:float仍会占据位置,而position:absolute会覆盖文档流中其他元 ...
- svg技术(可缩放矢量图形)介绍
公司里面的产品用图表的地方也比较多,作为平台维护的我,收到几次需求提的建议中包括图表美化的功能,要炫,要3d,立体感,功能要强大等到:平台现有控件都是用的一个开源flash,我对flash虽然会一点但 ...
- HTML5: SVG (可缩放矢量图形)
ylbtech-HTML5: SVG (可缩放矢量图形) 可缩放矢量图形是基于可扩展标记语言(标准通用标记语言的子集),用于描述二维矢量图形的一种图形格式.它由万维网联盟制定,是一个开放标准. 1. ...
随机推荐
- Spring框架系列(二)--装配和注入Bean
企业日常开发中,几乎都是Spring系的框架,无论是SSM.还是现在大火的SpringBoot+JPA/MyBatis,使用最大的目的就是简化开发 基本模块: 核心容器:Beans.Core.Cont ...
- valgrind检查代码内存泄漏,5种内存泄漏情况
摘要: valgrind是linux下用于调试程序和查找内存泄露的常用工具.valgrind会报告5种内存泄露,"definitely lost", "indirectl ...
- no bundle URL present in react-native?
Assuming that you are using nvm and multiple versions of node installed, here is the solution: Say t ...
- 洛谷——P3807 【模板】卢卡斯定理
P3807 [模板]卢卡斯定理 洛谷智推模板题,qwq,还是太弱啦,组合数基础模板题还没做过... 给定n,m,p($1\le n,m,p\le 10^5$) 求 $C_{n+m}^{m}\ mod\ ...
- Gym - 101670J Punching Power(CTU Open Contest 2017 最大独立集)
题目: The park management finally decided to install some popular boxing machines at various strategic ...
- Python习题之列表排序,4种方法
def sort_list_method_1(a): return sorted(a) print(sort_list_method_1([1, 4, 2])) def sort_list_metho ...
- Python基础函数
join()函数的用法 join()函数连接字符串数组.将字符串.元组.列表中的元素以指定的字符(分隔符)连接生成一个新的字符串 语法:'sep'.join(seq) 参数说明sep:分隔符.可以为空 ...
- Python基础—面向对象(初级篇)
一.什么是面向对象编程 面向对象编程(Object Oriented Programming,OOP,面向对象程序设计),python语言比较灵活即支持面向对象编程也支持面向函数式编程. 面向过程编程 ...
- 【6572】关于mtk平台display模块的学习探讨
现在在学习mtk的display subsystem,有遇到流程上不太清楚地地方想要询问: 1.cmd模式和video模式framebuffer如何更新, 以及两种模式的差异? cmd和video m ...
- spark之scala快速入门
scala和java都是在jvm之上的语言,相对来讲,scala热度比较低,其实并不是一个特别好的语言选择. 原因倒不是因为scala本身的缺点,而是使用人群不够多,论坛和社区不够活跃.这就跟社交软件 ...
