cf396B On Sum of Fractions

Let's assume that

• v(n) is the largest prime number, that does not exceed n;
• u(n) is the smallest prime number strictly greater than n.

Find .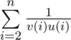

Input

The first line contains integer t (1 ≤ t ≤ 500) — the number of testscases.

Each of the following t lines of the input contains integer n (2 ≤ n ≤ 10⁹).

Output

Print t lines: the i-th of them must contain the answer to the i-th test as an irreducible fraction "p/q", where p, q are integers, q > 0.

Examples

Input

2
2
3

Output

1/6
7/30

写写1/v(i)u(i)的前几项就能发现规律

i    2   3   4   5

v   2   3   3   5

u   3   5   5   7

如果用个f(i)表示1/v(i)u(i)，那么对于一个质数x，有f(2)+f(3)+...+f(x-1)=1/2-1/x

然后在对于一个夹在两质数a,b之间的x，显然从a到x的f值都是a/b，所以就是找到n前后最近的质数，把两分式通分一下就好了

这里我是直接n往前往后Miller-Robin找第一个质数，不过sqrt(n)的暴力应该也能卡过去？

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<algorithm>
 #include<cmath>
 #include<queue>
 #include<deque>
 #include<set>
 #include<map>
 #include<ctime>
 #define LL long long
 #define inf 0x7ffffff
 #define pa pair<int,int>
 #define mkp(a,b) make_pair(a,b)
 #define pi 3.1415926535897932384626433832795028841971
 using namespace std;
 inline LL read()
 {
     LL x=,f=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 LL mul(LL x,LL n,LL MOD)
 {
     LL res=x*n-(LL)((long double) x*n/MOD+0.5)*MOD;
     while (res<)res+=MOD;
     while (res>=MOD)res-=MOD;
     return res;
 }
 LL qpow(LL x,LL n,LL MOD)
 {
     x=(x%MOD+MOD)%MOD;
     LL p=x,con=;
     while (n)
     {
         if (n&)con=mul(con,p,MOD);
         p=mul(p,p,MOD);
         n>>=;
     }
     return con;
 }
 bool witness(LL a,LL b)
 {
     if (a==b)return true;
     LL s=b-;
     int t=;
     while (!(s&))s>>=,t++;
     LL x=qpow(a,s,b);
     if (x==)return ;
     while (t--)
     {
         if (x==b-)return true;
         x=mul(x,x,b);
         if (x==)return false;
     }
     return false;
 }
 bool isprime(LL x)
 {
     if (x==||x==)return false;
     static int p[]={,,,,,,,,,,};
     for (int i=;i<=;i++)
         if (!witness(p[i],x))return false;
     return true;
 }
 inline LL gcd(LL a,LL b)
 {
     if (a<b)swap(a,b);
     return b==?a:gcd(b,a%b);
 }
 int main()
 {
     int T=read();
     while (T--)
     {
         LL x=read(),y,z,t,ans1,ans2;
         for (y=x;y>=;y--)if (isprime(y))break;
         for (z=x+;z<=1e9+;z++)if (isprime(z))break;
         //ans=1/2-1/y+(x-y+1)*y/z
         ans1=y*z-*z+*x-*y+;ans2=*y*z;
         t=gcd(ans1,ans2);ans1/=t;ans2/=t;
         printf("%lld/%lld\n",ans1,ans2);
     }
 }

cf396B