JS实现最短路径之迪杰斯特拉(Dijkstra)算法

最短路径：

　　对于网图来说，最短路径是指两个顶点之间经过的边上权值和最少的路径，我们称第一个顶点是源点，最后一个顶点是终点

迪杰斯特拉 ( Dijkstra) 算法是并不是一下子就求出 了 Vo 到V8 的最短路径，而是一步步求出它们之间顶点的最短路径，过程中都是基于已经求出的最短路径的基础上，求得更远顶点的最短路径，最终得到你要的结果

 

JS代码：

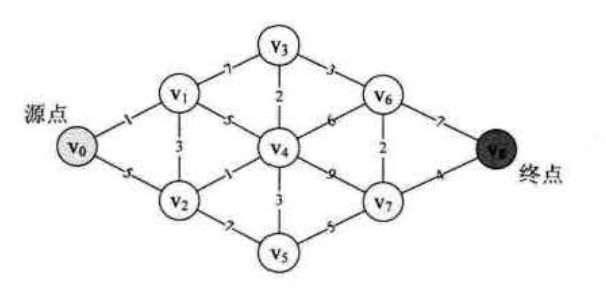
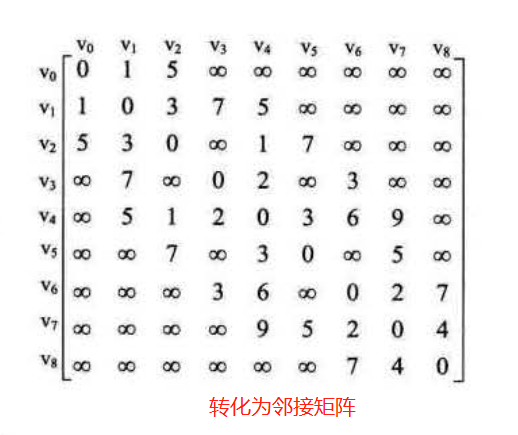
//定义邻接矩阵
let Arr2 = [
    [0, 1, 5, 65535, 65535, 65535, 65535, 65535, 65535],
    [1, 0, 3, 7, 5, 65535, 65535, 65535, 65535],
    [5, 3, 0, 65535, 1, 7, 65535, 65535, 65535],
    [65535, 7, 65535, 0, 2, 65535, 3, 65535, 65535],
    [65535, 5, 1, 2, 0, 3, 6, 9, 65535],
    [65535, 65535, 7, 65535, 3, 0, 65535, 5, 65535],
    [65535, 65535, 65535, 3, 6, 65535, 0, 2, 7],
    [65535, 65535, 65535, 65535, 9, 5, 2, 0, 4],
    [65535, 65535, 65535, 65535, 65535, 65535, 7, 4, 0],
]

let numVertexes = 9, //定义顶点数
    numEdges = 15; //定义边数

// 定义图结构
function MGraph() {
    this.vexs = []; //顶点表
    this.arc = []; // 邻接矩阵，可看作边表
    this.numVertexes = null; //图中当前的顶点数
    this.numEdges = null; //图中当前的边数
}
let G = new MGraph(); //创建图使用

//创建图
function createMGraph() {
    G.numVertexes = numVertexes; //设置顶点数
    G.numEdges = numEdges; //设置边数

    //录入顶点信息
    for (let i = 0; i < G.numVertexes; i++) {
        G.vexs[i] = 'V' + i; //scanf('%s'); //ascii码转字符 //String.fromCharCode(i + 65);
    }
    console.log(G.vexs) //打印顶点

    //邻接矩阵初始化
    for (let i = 0; i < G.numVertexes; i++) {
        G.arc[i] = [];
        for (j = 0; j < G.numVertexes; j++) {
            G.arc[i][j] = Arr2[i][j]; //INFINITY;
        }
    }
    console.log(G.arc); //打印邻接矩阵
}

let Pathmatirx = [] // 用于存储最短路径下标的数组，下标为各个顶点，值为下标顶点的前驱顶点
let ShortPathTable = [] //用于存储到各点最短路径的权值和

function Dijkstra() {
    let k, min;
    let final = [];
    for (let v = 0; v < G.numVertexes; v++) {
        final[v] = 0;
        ShortPathTable[v] = G.arc[0][v];
        Pathmatirx[v] = 0;
    }
    ShortPathTable[0] = 0;
    final[0] = 1;

    for (let v = 1; v < G.numVertexes; v++) { //初始化数据
        min = 65535;
        for (let w = 0; w < G.numVertexes; w++) { //寻找离V0最近的顶点
            if (!final[w] && ShortPathTable[w] < min) {
                k = w;
                min = ShortPathTable[w]; //w 顶点离V0顶点更近
            }
        }
        final[k] = 1; //将目前找到的最近的顶点置位1
        for (let w = 0; w < G.numVertexes; w++) { //修正当前最短路径及距离
            if (!final[w] && (min + G.arc[k][w] < ShortPathTable[w])) { //说明找到了更短的路径，修改Pathmatirx[w]和ShortPathTable[w]
                ShortPathTable[w] = min + G.arc[k][w];
                Pathmatirx[w] = k;
            }
        }
    }
}

function PrintVn(Vn) {
    //打印V0-Vn最短路径
    console.log("%s-%s 最小权值和: %d", G.vexs[0], G.vexs[Vn], ShortPathTable[Vn]);
    //打印最短路线
    let temp = Vn,
        str = '';
    while (temp != 0) {
        str = '->' + G.vexs[temp] + str
        temp = Pathmatirx[temp]
    }
    str = 'V0' + str;
    console.log('最短路线：'+str);
}

createMGraph();
Dijkstra();
PrintVn(8);

运行结果：

迪杰斯特拉 ( Dijkstra) 算法是 一个按路径长度递增的次序产生最短路径的算法。时间复杂度为 O(n2)，n为顶点个数，如果是从其他顶点开始，那么在原有算法的基础上再来一次循环，此时的时间复杂度为O(n3)。