Leetcode之动态规划（DP）专题-877. 石子游戏（Stone Game）

Leetcode之动态规划（DP）专题-877. 石子游戏（Stone Game）

---

亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行，每堆都有正整数颗石子 piles[i] 。

游戏以谁手中的石子最多来决出胜负。石子的总数是奇数，所以没有平局。

亚历克斯和李轮流进行，亚历克斯先开始。 每回合，玩家从行的开始或结束处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止，此时手中石子最多的玩家获胜。

假设亚历克斯和李都发挥出最佳水平，当亚历克斯赢得比赛时返回 true ，当李赢得比赛时返回 false 。

示例：

输入：[5,3,4,5]
输出：true
解释：
亚历克斯先开始，只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗，这一行就变成了 [3,4,5] 。
如果李拿走前 3 颗，那么剩下的是 [4,5]，亚历克斯拿走后 5 颗赢得 10 分。
如果李拿走后 5 颗，那么剩下的是 [3,4]，亚历克斯拿走后 4 颗赢得 9 分。
这表明，取前 5 颗石子对亚历克斯来说是一个胜利的举动，所以我们返回 true 。

提示：

1. 2 <= piles.length <= 500
2. piles.length 是偶数。
3. 1 <= piles[i] <= 500
4. sum(piles) 是奇数。

---

数学题，但我们用DP来求解这一题。

我们首先定义一个类，名为P：

private static class P {
        int fir, sec;

        P(int fir, int sec) {
            this.fir = fir;
            this.sec = sec;
        }
    }

P中有两个属性，fir代表先手获得的最高分数，sec代表后手获得的最高分数

那么我们就可以写出DP的含义

我们把dp定义为2维，如dp[i][j]代表从这堆石子的第i堆选到第j堆中获得的最高分数。

那么dp[i][j].fir 表示从第i堆到第j堆中先手获得的最高分。

dp[i][j].sec 表示从第i堆到第j堆中后手获得的最高分。

例如：piles = [5，3，4，5]

dp[0][1].fir = 5, 面对[5,3]，先手可以得5分

dp[0][1].sec = 3，面对[5,3],后手可以得3分

我们首先明确一点，当 i == j 时，即只有一堆石子的时候，上面的例子，例如 i == j == 0 那么 dp[i][j].fir = 5 sec=0

所以我们把i==j时的所有情况，遍历一遍。

for (int i = 0; i < n; i++) {
            dp[i][i].fir = piles[i];
            dp[i][i].sec = 0;
}

下面看一张图，是最终dp数组的最后状态：

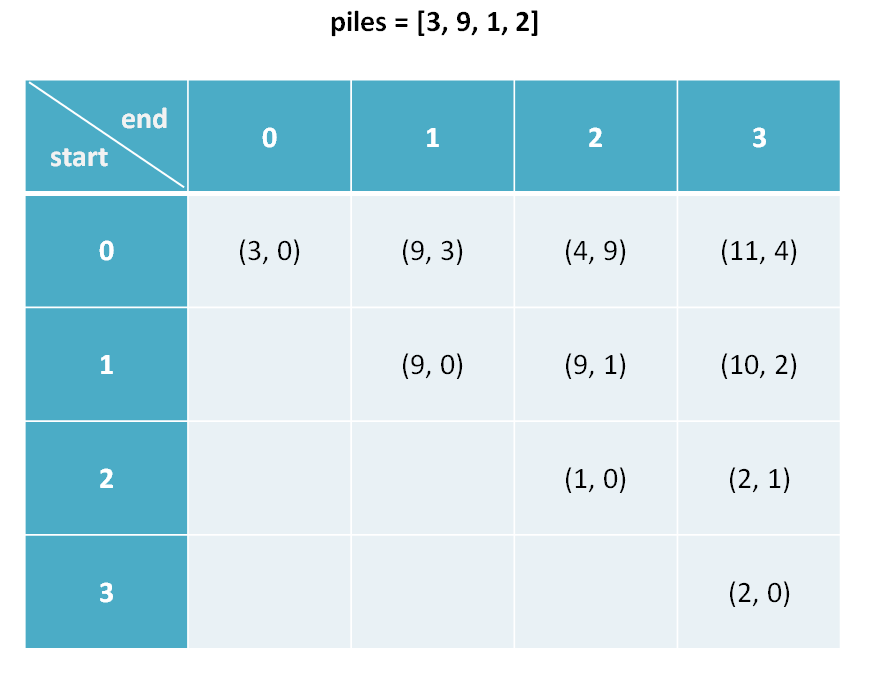
我们可以看到，dp[0][1] = （9，3）    即dp[0][1].fir = 9    sec=3

这个数值是由（0，0）和（1，1）一起生成的。

我们可以按层遍历，即：

第1层：对角线

第2层：（9，3） （9，1） （2，1）

第3层：（4，9） （10，2）

第4层：（11，4）

选择了按层遍历后，我们需要得到状态转移方程：

面对一堆石头，我们有如下情况可以选择：

1、我是先手

• 我选左边，面对剩下的piles[i+1,j]
• 我选右边，面对剩下的piles[i,j-1]

随后对方变成先手，我变成后手

dp[i][j].fir = max(piles[i]+dp[i+1][j].sec,piles[j]+dp[i][j-1].sec);

2、我是后手

• 先手选择了左边的那堆，我只能选择剩下的，dp[i][j].sec = dp[i+1][j].fir;
• 先手选择了右边的那堆，我只能选择剩下的，dp[i][j].sec = dp[i][j-1].fir;

随后对方变成后手，我变成了先手

---

class Solution {
    private static class P {
        int fir, sec;

        P(int fir, int sec) {
            this.fir = fir;
            this.sec = sec;
        }
    }

    public boolean stoneGame(int[] piles) {

        int n = piles.length;
        P[][] dp = new P[n + 1][n + 1];
        for (int i = 0; i < n; i++) {
            for (int j = i; j < n; j++) {
                dp[i][j] = new P(0, 0);
            }
        }
        for (int i = 0; i < n; i++) {
            dp[i][i].fir = piles[i];
            dp[i][i].sec = 0;
        }

        for (int c = 2; c <= n; c++) {
            for (int i = 0; i <= n - c; i++) {
                int j = c + i - 1;
                int left = piles[i] + dp[i + 1][j].sec;
                int right = piles[j] + dp[i][j - 1].sec;
                if (left > right) {
                    dp[i][j].fir = left;
                    dp[i][j].sec = dp[i + 1][j].fir;
                } else {
                    dp[i][j].fir = right;
                    dp[i][j].sec = dp[i][j - 1].fir;
                }

            }
        }
        return dp[0][n - 1].fir > dp[0][n - 1].sec;
    }
}

#本题思路来自题解区