hdu 5651 重复全排列+逆元

知识点：

n个元素，其中a1，a2，····，an互不相同，进行全排列，可得n!个不同的排列。

若其中某一元素ai重复了ni次，全排列出来必有重复元素，其中真正不同的排列数应为 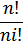，即其重复度为ni!

同理a1重复了n1次，a2重复了n2次，····，ak重复了nk次，n1+n2+····+nk=n。

对于这样的n个元素进行全排列，可得不同排列的个数实际上是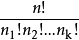 

由于题目要求是对100000007取余 同余定理中对于同一个除数，两个数的乘积与它们余数的乘积同余。但这里有除法所以得用上逆元

逆元

• 定义： 
  满足a*k≡1 (mod p)的k值就是a关于p的乘法逆元。eg: 1=5*3-14 所以5关于模14的乘法逆元为3.

• 应用： 
  当我们要求 (a/b) mod P 的值时，如果 a 很大，无法直接求得a/b的值时，我们就可以使用乘法逆元。我们可以通过求b关于P的乘法逆元k，将a乘上k再模P，即(a%P*k)。其结果与(a/b) mod P等价。

关于逆元的求解方法日后在做总结  这里用的是exgcd

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long LL;
const LL MOD=1e9+;
int cnt[];
char ch[];

LL jiecheng(int n)
{
    if(n==)
        return ;
    LL ans=;
    for(int i=;i<=n;i++)
        ans=ans*i%MOD;
    return ans;
}

LL x,y;
LL gcd(LL a,LL b)
{
    LL t,d;
    if(b==)
    {
         x=,y=;
         return a;
    }
     d=gcd(b,a%b);
     t=x, x=y, y=t-(a/b)*y;
     return d;
 }

int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        memset(cnt,,sizeof(cnt));
        scanf("%s",ch);
        int len=strlen(ch);
        for(int i=;i<len;i++)
        {
            cnt[ch[i]-' ']++;
        }
        int count=;
        for(int i=;i<;i++)
        {
            if(cnt[i]&)
                count++;
            cnt[i]/=;
        }
        if(count>)
        {
            cout<<<<endl;
            continue;
        }
        LL ans=jiecheng(len/)%MOD;
        for(int i=;i<;i++)
        {
            if(cnt[i]>)
            {
                gcd(jiecheng(cnt[i]),MOD);
                if(x<)
                    x+=MOD;// 求逆元
                ans=ans*x%MOD;
            }
        }
        cout<<ans<<endl;
    }
}