Java实现二叉树地遍历、求深度和叶子结点的个数

一、分析

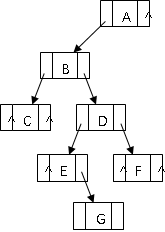
　　二叉树是n个结点所构成的集合，它或为空树，或为非空树。对于非空树，它有且仅有一个根结点，且除根结点以外的其余结点分为两个互不相交的子集，分别称为左子树和右子树，它们本身又都是二叉树。

　　显而易见，二叉树具有递归的性质，因此表示二叉树的结点至少要包含3个域：数据域、左指针、右指针。在Java中，我们可以将二叉树的结点视为一个类，其中含有左子树地址、右子树地址和数据三个属性，每个结点即使类的实例化对象。因为二叉树的递归性质，所以我们可以通过递归来实现二叉树地求深度、求叶子结点的个数、先序、中序、后序遍历，而层序遍历则可以通过队列来实现。

二、实现

1、定义结点类

 class InitBiTree{

     private String data = null;

     private InitBiTree lchild = null;

     private InitBiTree rchild = null;

     public String getData() {
         return data;
     }

     public void setData(String data) {
         this.data = data;
     }

     public InitBiTree getLchild() {
         return lchild;
     }

     public void setLchild(InitBiTree lchild) {
         this.lchild = lchild;
     }

     public InitBiTree getRchild() {
         return rchild;
     }

     public void setRchild(InitBiTree rchild) {
         this.rchild = rchild;
     }
 }

2、定义方法类

 class Tools{
     public static InitBiTree createBiTree() {  　　　　　　　　　　　　　　　　//先序遍历创建二叉树
         System.out.print("请按先序次序依次输入二叉树的值，#号表示建立空树：");
         Scanner sc = new Scanner(System.in);
         String input = null;
         input = sc.next();
         if(input.equals("#")) {
             return null;
         }else {
             InitBiTree initBiTree = new InitBiTree();
             initBiTree.setData(input);
             initBiTree.setLchild(Tools.createBiTree());
             initBiTree.setRchild(Tools.createBiTree());
             return initBiTree;
         }
     }

     public static void preOrderTraverse(InitBiTree initBiTree) { 　　　　 //先序遍历
         if(initBiTree != null) {
             System.out.print(initBiTree.getData());
             Tools.preOrderTraverse(initBiTree.getLchild());
             Tools.preOrderTraverse(initBiTree.getRchild());
         }
     }

     public static void inOrderTraverse(InitBiTree initBiTree) {  　　　 　//中序遍历
         if(initBiTree != null) {
             Tools.inOrderTraverse(initBiTree.getLchild());
             System.out.print(initBiTree.getData());
             Tools.inOrderTraverse(initBiTree.getRchild());
         }
     }

     public static void postOrderTraverse(InitBiTree initBiTree) {  　　　 //后序遍历
         if(initBiTree != null) {
             Tools.postOrderTraverse(initBiTree.getLchild());
             Tools.postOrderTraverse(initBiTree.getRchild());
             System.out.print(initBiTree.getData());
         }
     }

     public static void levelOrderTraverse(InitBiTree initBiTree) {  　　　//层序遍历
         if(initBiTree != null) {
             LinkedList<InitBiTree> linkedList = new LinkedList<InitBiTree>();
             linkedList.offer(initBiTree);
             while(!linkedList.isEmpty()) {
                 initBiTree = linkedList.poll();
                 if(initBiTree.getLchild() != null) {
                     linkedList.offer(initBiTree.getLchild());
                 }
                 if(initBiTree.getRchild() != null) {
                     linkedList.offer(initBiTree.getRchild());
                 }
                 System.out.print(initBiTree.getData());
             }
         }
     }

     public static int biTreeDepth(InitBiTree initBiTree) {  　　　　　　　　//求二叉树深度
         if(initBiTree != null) {
             int l = Tools.biTreeDepth(initBiTree.getLchild());
                     int r = Tools.biTreeDepth(initBiTree.getRchild());
                     if(l > r) {
                         return l + 1;
                     }else {
                             return r + 1;
                     }
         }else {
             return 0;
         }
     }

     public static int biTreeNodeCount(InitBiTree initBiTree) {  　　　　　//求叶节点个数
         if(initBiTree != null) {
             int l = Tools.biTreeNodeCount(initBiTree.getLchild());
             int r = Tools.biTreeNodeCount(initBiTree.getRchild());
             if(l == 0 && r == 0) {
                 return 1;
             }else {
                 return l + r;
             }
         }else {
             return 0;
         }
     }
 }

3、主函数调用

 package word7;

 import java.util.LinkedList;
 import java.util.Scanner;

 public class Main {

     public static void main(String[] args) {
         InitBiTree initBiTree = Tools.createBiTree();
         System.out.println("——————先序遍历——————");
         Tools.preOrderTraverse(initBiTree);
         System.out.println();
         System.out.println("——————中序遍历——————");
         Tools.inOrderTraverse(initBiTree);
         System.out.println();
         System.out.println("——————后序遍历——————");
         Tools.postOrderTraverse(initBiTree);
         System.out.println();
         System.out.println("——————层序遍历——————");
         Tools.levelOrderTraverse(initBiTree);
         System.out.println();
         System.out.println("——————二叉树深度——————");
         System.out.println(Tools.biTreeDepth(initBiTree));
         System.out.println("——————叶子结点个数——————");
         System.out.println(Tools.biTreeNodeCount(initBiTree));
     }

 }

三、运行截图