poj2002 hash+邻接表优化Squares

Squares

Time Limit: 3500MS		Memory Limit: 65536K
Total Submissions: 17487		Accepted: 6643

Description

A square is a 4-sided polygon whose sides have equal length and adjacent sides form 90-degree angles. It is also a polygon such that rotating about its centre by 90 degrees gives the same polygon. It is not the only polygon with the latter property, however, as a regular octagon also has this property.

So we all know what a square looks like, but can we find all
possible squares that can be formed from a set of stars in a night sky?
To make the problem easier, we will assume that the night sky is a
2-dimensional plane, and each star is specified by its x and y
coordinates.

Input

The
input consists of a number of test cases. Each test case starts with the
integer n (1 <= n <= 1000) indicating the number of points to
follow. Each of the next n lines specify the x and y coordinates (two
integers) of each point. You may assume that the points are distinct and
the magnitudes of the coordinates are less than 20000. The input is
terminated when n = 0.

Output

For each test case, print on a line the number of squares one can form from the given stars.

Sample Input

4
1 0
0 1
1 1
0 0
9
0 0
1 0
2 0
0 2
1 2
2 2
0 1
1 1
2 1
4
-2 5
3 7
0 0
5 2
0

Sample Output

1
6
1

Source

大致题意：

有一堆平面散点集，任取四个点，求能组成正方形的不同组合方式有多少。

相同的四个点，不同顺序构成的正方形视为同一正方形。

解题思路：

做本题数学功底要很强= =

直接四个点四个点地枚举肯定超时的，不可取。

普遍的做法是：先枚举两个点，通过数学公式得到另外2个点，使得这四个点能够成正方形。然后检查散点集中是否存在计算出来的那两个点，若存在，说明有一个正方形。

但这种做法会使同一个正方形按照不同的顺序被枚举了四次，因此最后的结果要除以4.

已知： (x1,y1)  (x2,y2)

则：   x3=x1+(y1-y2)   y3= y1-(x1-x2)

x4=x2+(y1-y2)   y4= y2-(x1-x2)

或

x3=x1-(y1-y2)   y3= y1+(x1-x2)

x4=x2-(y1-y2)   y4= y2+(x1-x2)

据说是利用全等三角形可以求得上面的公式

有兴趣的同学可以证明下。。。

再来就是利用hash[]标记散点集了

我个人推荐key值使用 平方求余法

即标记点x y时，key = (x^2+y^2)%prime

此时key值的范围为[0, prime-1]

由于我个人的标记需求，我把公式更改为key = (x^2+y^2)%prime+1

使得key取值范围为[1, prime]，则hash[]大小为 hash[prime]

其中prime为 小于 最大区域长度（就是散点个数）n的k倍的最大素数，

即小于k*n 的最大素数 （k∈N*）

 

为了尽量达到key与地址的一一映射，k值至少为1，

当为k==1时，空间利用率最高，但地址冲突也相对较多，由于经常要为解决冲突开放寻址，使得寻找key值耗时O(1)的情况较少

当n太大时，空间利用率很低，但由于key分布很离散，地址冲突也相对较少，使得寻找键值耗时基本为O(1)的情况

提供一组不同k值的测试数据

K==1,   prime=997    1704ms

K==2,   prime=1999   1438ms

K==8,   prime=7993   1110ms

K==10,  prime=9973   1063ms

K==30,  prime=29989  1000ms

K==50,  prime=49999  1016ms

K==100, prime=99991  1000ms

最后解决的地址冲突的方法，这是hash的难点。我使用了 链地址法

typedef class HashTable

{

public:

int x,y;   //标记key值对应的x,y

HashTable* next;  //当出现地址冲突时，开放寻址

HashTable()  //Initial

{

next=0;

}

}Hashtable;

Hashtable* hash[prime];   //注意hash[]是指针数组，存放地址

//hash[]初始化为NULL (C++初始化为0)

先解释所谓的“冲突”

本题对于一组（x，y），通过一个函数hash(x，y)，其实就是上面提到的key的计算公式

key = (x^2+y^2)%prime+1

于是我们得到了一个关于x,y的key值，但是我们不能保证key与每一组的(x,y)都一一对应，即可能存在 hash(x1，y1) = hash(x2，y2) = key

处理方法：

(1) 当读入(x1, y1)时，若hash[key]为NULL，我们直接申请一个临时结点Hashtable* temp，记录x1,y1的信息，然后把结点temp的地址存放到hash[key]中

此后我们就可以利用key访问temp的地址，继而得到x1,y1的信息

(2) 当读入(x2, y2)时，由于hash(x1，y1) = hash(x2，y2) = key，即(x2, y2)的信息同样要存入hash[key]，但hash[key]已存有一个地址，怎么办？

注意到hash[key]所存放的temp中还有一个成员next，且next==0，由此，我们可以申请一个新结点存放x2,y2的信息，用next指向这个结点

此后我们利用key访问temp的地址时，先检查temp->x和temp->y是否为我们所需求的信息，若不是，检查next是否非空，若next非空，则检查下一结点，直至 next==0

当检查完所有next后仍然找不到所要的信息，说明信息原本就不存在

就是说hash[key]只保存第一个值为key的结点的地址，以后若出现相同key值的结点，则用前一个结点的next保存新结点的地址，其实就是一个链表

简单的图示为：

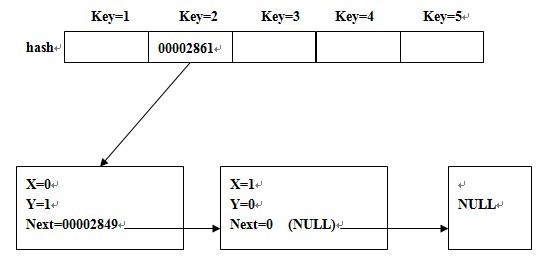
#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=;
const int mod=;
int ptx[maxn],pty[maxn];
int cur,ans;
int first[maxn];
struct node{
   int x,y;
   int next;
}que[];

void insert(int x,int y){
    int h=(x*x+y*y)%mod;
    que[cur].x=x;
    que[cur].y=y;
    que[cur].next=first[h];
    first[h]=cur;
    cur++;
}

bool find(int tx,int ty){
     int h=(tx*tx+ty*ty)%mod;
     int next=first[h];
     while(next!=-){
        if(que[next].x==tx&&que[next].y==ty)
            return true;
            next=que[next].next;
     }
     return false;

}

int main(){
    int n;
    while(scanf("%d",&n)!=EOF){
        if(n==)
        break;
            cur=,ans=;
        memset(ptx,,sizeof(ptx));
        memset(pty,,sizeof(pty));
        memset(first, -,sizeof(first));
        for(int i=;i<n;i++){
            scanf("%d%d",&ptx[i],&pty[i]);
            insert(ptx[i],pty[i]);
        }
       for (int i = ; i < n; ++i){
            for (int j = i + ; j < n; ++j){
                int x1 = ptx[i] - (pty[i] - pty[j]);
                int y1 = pty[i] + (ptx[i] - ptx[j]);
                int x2 = ptx[j] - (pty[i] - pty[j]);
                int y2 = pty[j] + (ptx[i] - ptx[j]);
                if (find(x1, y1) && find(x2, y2))
                    ++ans;
            }
        }
        for (int i = ; i < n; ++i){
            for (int j = i + ; j < n; ++j){
                int x1 = ptx[i] + (pty[i] - pty[j]);
                int y1 = pty[i] - (ptx[i] - ptx[j]);
                int x2 = ptx[j] + (pty[i] - pty[j]);
                int y2 = pty[j] - (ptx[i] - ptx[j]);
                if (find(x1, y1) && find(x2, y2))
                    ++ans;
            }
        }
               ans=ans/;
               printf("%d\n",ans);
    }
    return ;
}