【离线 线段树分治】bzoj4025: 二分图

昨天mac的gdb挂了，今天怎么笔记本的gdb也挂了……

Description

神犇有一个n个节点的图。因为神犇是神犇，所以在T时间内一些边会出现后消失。神犇要求出每一时间段内这个图是否是二分图。这么简单的问题神犇当然会做了，于是他想考考你。

Input

输入数据的第一行是三个整数n,m,T。

第2行到第m+1行，每行4个整数u,v,start,end。第i+1行的四个整数表示第i条边连接u,v两个点，这条边在start时刻出现，在第end时刻消失。

Output

输出包含T行。在第i行中，如果第i时间段内这个图是二分图，那么输出“Yes”，否则输出“No”，不含引号。

Sample Input

3 3 3
1 2 0 2
2 3 0 3
1 3 1 2

Sample Output

Yes
No
Yes

HINT

样例说明：

0时刻，出现两条边1-2和2-3。

第1时间段内，这个图是二分图，输出Yes。

1时刻，出现一条边1-3。

第2时间段内，这个图不是二分图，输出No。

2时刻，1-2和1-3两条边消失。

第3时间段内，只有一条边2-3，这个图是二分图，输出Yes。

数据范围：

n<=100000，m<=200000，T<=100000，1<=u,v<=n，0<=start<=end<=T。

---

题目分析

线段树分治一样的套路

重点在于如何判断一张图是否是二分图。我们知道二分图的充要条件是无奇环的森林：那么奇环的成立条件是在并查集合并时，所连边的两个点在原树中的路径长度为偶数。用$d[x]$表示$x$点在并查集结构中，到其父亲的路径奇偶性；初始每个点独自为根，则$d[x]=0$。每当两个不同的集合合并时，就应该 d[fx]=get(x)^get(y)^ ，相当于是在并查集中维护了原图的结构。

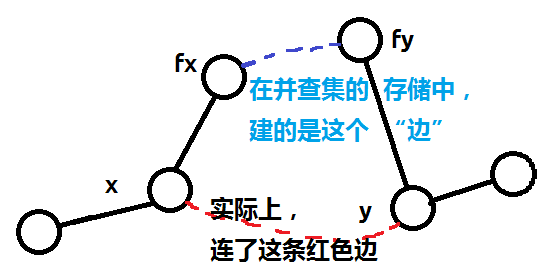
可以用以上这幅图理解。

第一遍写的时候，想当然地混淆了按秩合并并查集和原图这两个树形结构，get的时候直接^1地跳了。

 #include<bits/stdc++.h>
 const int maxn = ;
 const int maxm = ;
 const int maxt = ;
 const int maxOpt = ;

 int n,m,T;
 struct Edge
 {
     int u,v,s,t;
     Edge(int a=, int b=, int c=, int d=):u(a),v(b),s(c),t(d) {}
 }tmp;
 typedef std::vector<Edge> vec;
 struct Dsu
 {
     int top,fat[maxn],size[maxn],d[maxn];
     std::pair<int, int> stk[maxOpt];
     void init(){for (int i=; i<=n; i++) fat[i] = i, size[i] = ;}
     int find(int x){while (x!=fat[x]) x = fat[x];return x;}
     int get(int x){int ret = ;while(x!=fat[x]) ret ^= d[x], x = fat[x];return ret;}
     bool merge(int x, int y)
     {
         int fx = find(x), fy = find(y);
         if (fx==fy) return get(x)^get(y)^;
         if (size[fx] > size[fy]) std::swap(fx, fy);
         fat[fx] = fy, size[fy] += size[fx];
         d[fx] = get(x)^get(y)^;
         stk[++top] = std::make_pair(fx, fy);
         return ;
     }
     void cancel()
     {
         int x = stk[top].first, y = stk[top].second;
         fat[x] = x, size[y] -= size[x], --top, d[x] = ;
     }
 }dsu;
 bool ans[maxt];
 vec opt;

 int read()
 {
     char ch = getchar();
     int num = , fl = ;
     for (; !isdigit(ch); ch=getchar())
         if (ch=='-') fl = -;
     for (; isdigit(ch); ch=getchar())
         num = (num<<)+(num<<)+ch-;
     return num*fl;
 }
51 void solve(int l, int r, vec opt)
 {
     vec L,R;
     int mid = (l+r)>>, tmp = dsu.top;
     for (int i=, mx=opt.size(); i<mx; i++)
     {
         int s = opt[i].s, t = opt[i].t;
         if (s <= l&&r <= t){
             if (dsu.merge(opt[i].u, opt[i].v)){
                 while (tmp!=dsu.top) dsu.cancel();
                 return;
             }
         }else{
             if (s <= mid) L.push_back(opt[i]);
             if (t > mid) R.push_back(opt[i]);
         }
     }
     if (l==r) ans[l] = ;
     else solve(l, mid, L), solve(mid+, r, R);
     while (tmp!=dsu.top) dsu.cancel();
 }
 int main()
 {
     n = read(), m = read(), T = read(), dsu.init();
     for (int i=; i<=m; i++)
     {
         tmp.u = read(), tmp.v = read(), tmp.s = read()+, tmp.t = read();
         if (tmp.s <= tmp.t) opt.push_back(tmp);
     }
     solve(, T, opt);
     for (int i=; i<=T; i++) puts(ans[i]?"Yes":"No");
     return ;
 }

END