poj 2007(凸包)

Scrambled Polygon

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 8005		Accepted: 3798

Description

A closed polygon is a figure bounded by a finite number of line segments. The intersections of the bounding line segments are called the vertices of the polygon. When one starts at any vertex of a closed polygon and traverses each bounding line segment exactly once, one comes back to the starting vertex.

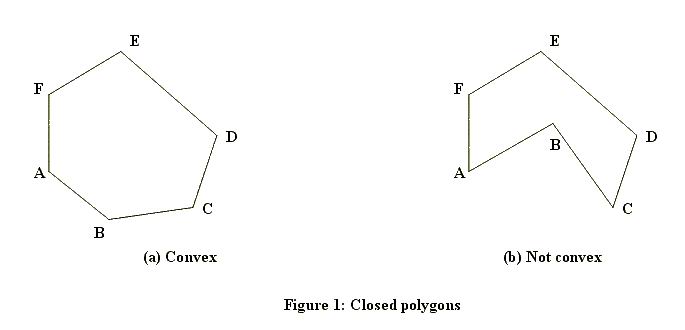
A closed polygon is called convex if the line segment joining any
two points of the polygon lies in the polygon. Figure 1 shows a closed
polygon which is convex and one which is not convex. (Informally, a
closed polygon is convex if its border doesn't have any "dents".)



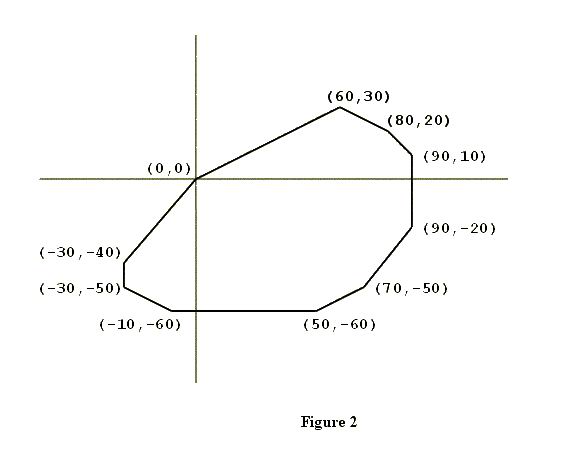
The subject of this problem is a closed convex polygon in the
coordinate plane, one of whose vertices is the origin (x = 0, y = 0).
Figure 2 shows an example. Such a polygon will have two properties
significant for this problem.

The first property is that the vertices of the polygon will be
confined to three or fewer of the four quadrants of the coordinate
plane. In the example shown in Figure 2, none of the vertices are in the
second quadrant (where x < 0, y > 0).

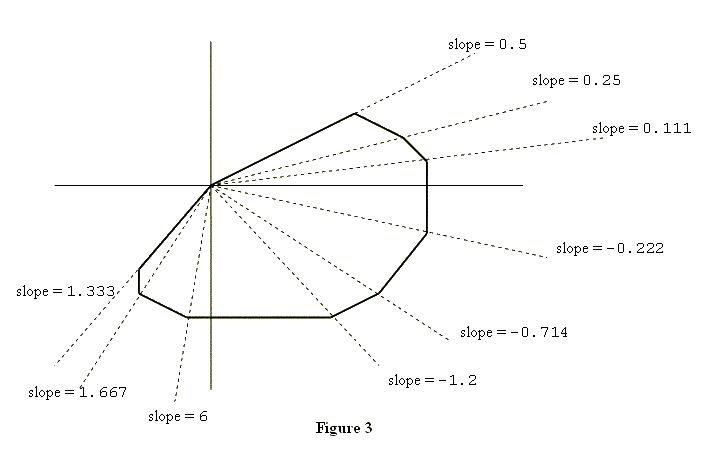
To describe the second property, suppose you "take a trip" around
the polygon: start at (0, 0), visit all other vertices exactly once, and
arrive at (0, 0). As you visit each vertex (other than (0, 0)), draw
the diagonal that connects the current vertex with (0, 0), and calculate
the slope of this diagonal. Then, within each quadrant, the slopes of
these diagonals will form a decreasing or increasing sequence of
numbers, i.e., they will be sorted. Figure 3 illustrates this point.

Input

The
input lists the vertices of a closed convex polygon in the plane. The
number of lines in the input will be at least three but no more than 50.
Each line contains the x and y coordinates of one vertex. Each x and y
coordinate is an integer in the range -999..999. The vertex on the first
line of the input file will be the origin, i.e., x = 0 and y = 0.
Otherwise, the vertices may be in a scrambled order. Except for the
origin, no vertex will be on the x-axis or the y-axis. No three vertices
are colinear.

Output

The
output lists the vertices of the given polygon, one vertex per line.
Each vertex from the input appears exactly once in the output. The
origin (0,0) is the vertex on the first line of the output. The order of
vertices in the output will determine a trip taken along the polygon's
border, in the counterclockwise direction. The output format for each
vertex is (x,y) as shown below.

Sample Input

0 0
70 -50
60 30
-30 -50
80 20
50 -60
90 -20
-30 -40
-10 -60
90 10

Sample Output

(0,0)
(-30,-40)
(-30,-50)
(-10,-60)
(50,-60)
(70,-50)
(90,-20)
(90,10)
(80,20)
(60,30)

题目要从(0,0)开始,所以找到(0,0)之后再进行输出其之后的和之前的就行...凸包水

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
const int N = ;
const double pi = atan(1.0)*;
const double eps = 1e-;
struct Point
{
    int x,y;
} p[N];
Point Stack[N];
int n;
int mult(Point a,Point b,Point c)
{
    return (a.x-c.x)*(b.y-c.y)-(a.y-c.y)*(b.x-c.x);
}
int dis(Point a,Point b)
{
    return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
int cmp(Point a,Point b)
{
    if(mult(a,b,p[])>) return ;
    if(mult(a,b,p[])==&&dis(b,p[])-dis(a,p[])>eps) return ;
    return ;
}
int Graham()
{
    int top = ;
    sort(p+,p+n,cmp);
    Stack[] = p[];
    Stack[] = p[];
    Stack[] = p[];
    for(int i=; i<n; i++)
    {
        while(top>=&&mult(p[i],Stack[top],Stack[top-])>=) top--;
        Stack[++top]=p[i];
    }
    return top;
}
int main()
{
    n = ;
    while(scanf("%d%d",&p[n].x,&p[n].y)!=EOF)
    {
        n++;
        //if(n==10) break;
    }
    //for(int i=0;i<n;i++) printf("%d %d\n",p[i].x,p[i].y);
    int k=;
    for(int i=; i<n; i++)
    {
        if(p[i].y<p[k].y||((p[i].y==p[k].y)&&(p[i].x<p[k].x))) k = i;
    }
    swap(p[],p[k]);
    double sum=;
    int top = Graham();
    int temp = ;
    for(int i=;i<=top;i++){
        if(Stack[i].x==&&Stack[i].y==) temp = i;
    }
    for(int i=temp;i<=top;i++) printf("(%d,%d)\n",Stack[i].x,Stack[i].y);
    for(int i=;i<temp;i++) printf("(%d,%d)\n",Stack[i].x,Stack[i].y);
}