（数据科学学习手札15）DBSCAN密度聚类法原理简介&Python与R的实现

DBSCAN算法是一种很典型的密度聚类法，它与K-means等只能对凸样本集进行聚类的算法不同，它也可以处理非凸集。

关于DBSCAN算法的原理，笔者觉得下面这篇写的甚是清楚练达，推荐大家阅读：

https://www.cnblogs.com/pinard/p/6208966.html

DBSCAN的主要优点有：

　　　　1） 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。

　　　　2） 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

　　　　3） 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

DBSCAN的主要缺点有：

　　　　1）如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

　　　　2） 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。

　　　　3） 调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。

R中的fpc包中封装了dbscan(data,eps,MinPts),其中data为待聚类的数据集，eps为距离阈值ϵ，MinPts为样本数阈值，这三个是必须设置的参数，无缺省项。

一、三种聚类算法在非凸样本集上的性能表现

下面我们以正弦函数为材料构造非凸样本集，分别使用DBSCAN、K-means、K-medoids算法进行聚类，并绘制最终的聚类效果图：

library(fpc)
library(cluster)

#构造非凸样本集
x1 <- seq(0,pi,0.01)
y1 <- sin(x1)+0.06*rnorm(length(x1))
y2 <- sin(x1)+0.06*rnorm(length(x1))+0.6
plot(x1,y1,ylim=c(0,2.0))
points(x1,y2)
c1 <- c(x1,x1)
c2 <- c(y1,y2)
data1 <- as.matrix(cbind(c1,c2))

构造的样本集如下：

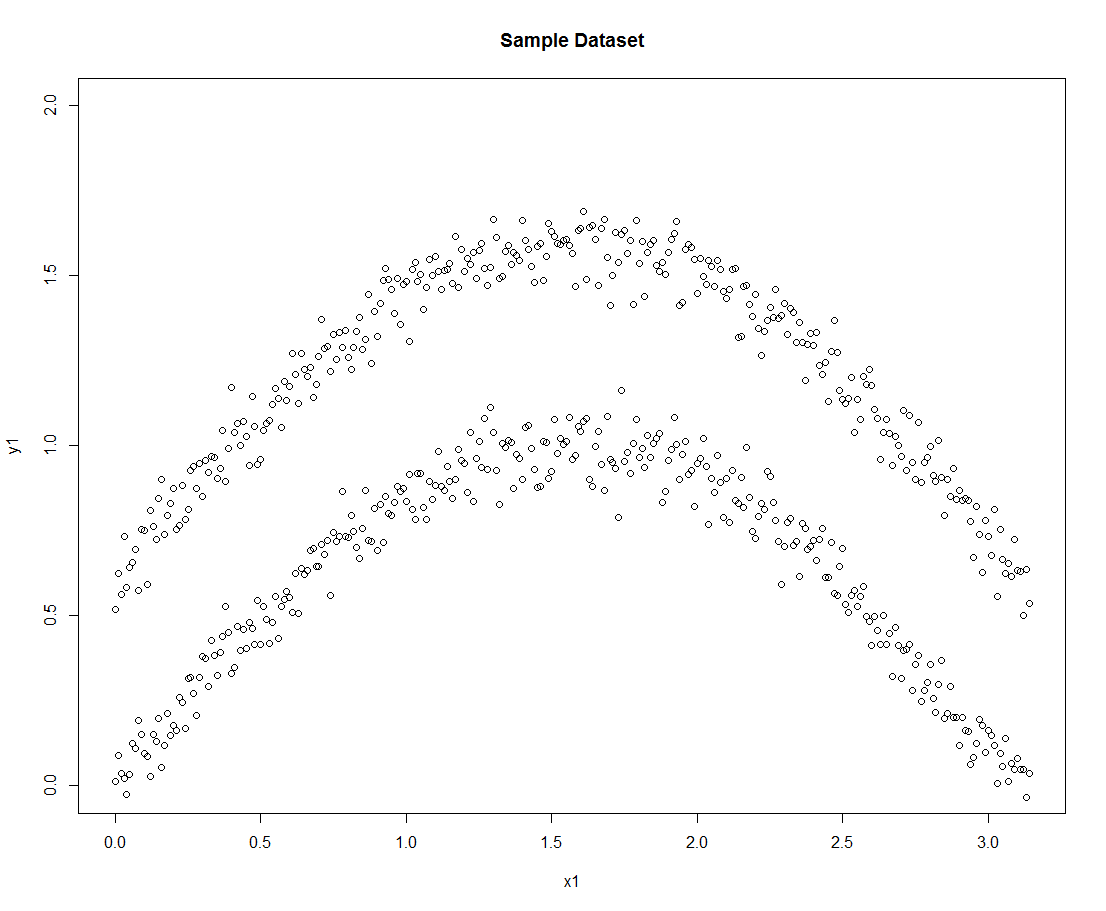
接着我们依次使用上述三种聚类算法：

#分别绘制三种聚类算法的聚类效果图
par(mfrow=c(1,3))
#DBSCAN聚类法
db <- dbscan(data1,eps=0.2,MinPts = 5)
db$cluster
plot(data1,col=db$cluster)
title('DBSCAN Cluster')
#K-means聚类法
km <- kmeans(data1,centers=2)
km$cluster
plot(data1,col=km$cluster)
title('K-means Cluster')
#K-medoids聚类法
pm <- pam(data1,k=2)
pm$clustering
plot(data1,col=pm$clustering)
title('K-medoids Cluster')

具体的聚类效果如下：

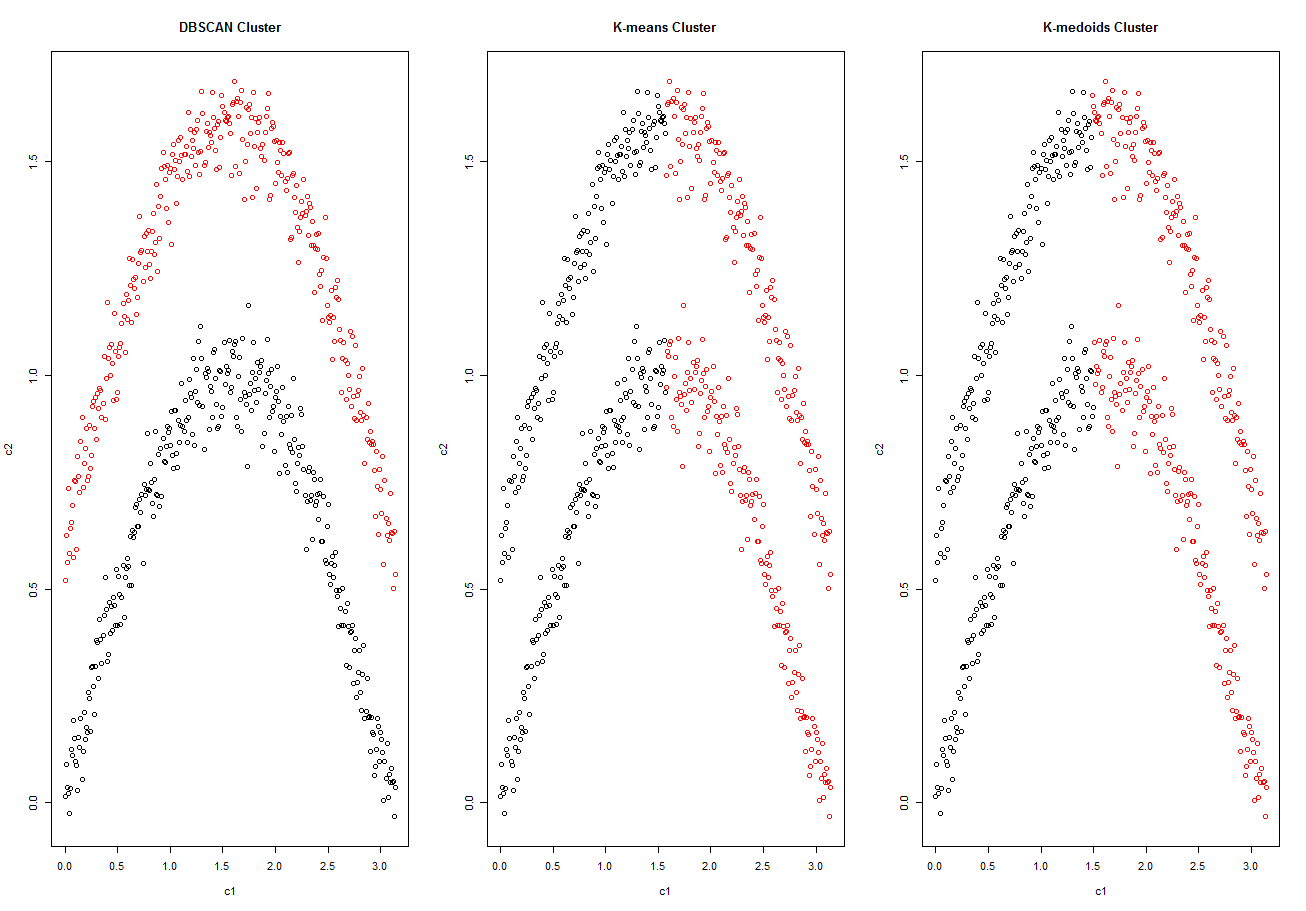
可以看出，在对非凸样本集的聚类上，DBSCAN效果非常好，而另外两种专门处理凸集的聚类算法就遇到了麻烦。

二、DBSCAN算法在常规凸样本集上的表现

上面我们研究了DBSCAN算法在非凸样本集上的表现，比K-means和K-medoids明显优秀很多，下面我们构造一个10维的凸样本集，具体的代码和聚类结果如下：

> library(fpc)
> library(Rtsne)
>
> #创建待聚类数据集
> data1 <- matrix(rnorm(10000,0,0.6),nrow=1000)
> data2 <- matrix(rnorm(10000,1,0.6),nrow=1000)
>
> data <- rbind(data1,data2)
>
> #对原高维数据集进行降维
> tsne <- Rtsne(data)
>
> par(mfrow=c(4,4))
> for(i in 1:16){
+   #进行DBSCAN聚类
+   db <- dbscan(data,eps=1.1+i*0.025,MinPts = 25)
+   #绘制聚类效果图
+   plot(tsne$Y[,1],tsne$Y[,2],col=db$cluster)
+   title(paste('eps=',as.character(1.1+i*0.025),sep=''))
+   print(paste('eps=',as.character(1.1+i*0.025)))
+   print(table(db$cluster))
+ }
[1] "eps= 1.125"

   0
2000
[1] "eps= 1.15"

   0    1    2
1950   26   24
[1] "eps= 1.175"

   0    1    2
1920   59   21
[1] "eps= 1.2"

   0    1    2
1834  120   46
[1] "eps= 1.225"

   0    1    2
1682  177  141
[1] "eps= 1.25"

   0    1    2
1515  250  235
[1] "eps= 1.275"

   0    1    2
1305  344  351
[1] "eps= 1.3"

   0    1    2
1163  425  412
[1] "eps= 1.325"

  0   1   2
989 521 490
[1] "eps= 1.35"

  0   1   2
854 596 550
[1] "eps= 1.375"

  0   1   2
707 670 623
[1] "eps= 1.4"

  0   1   2
572 732 696
[1] "eps= 1.425"

  0   1   2
500 766 734
[1] "eps= 1.45"

   0    1
 420 1580
[1] "eps= 1.475"

   0    1
 355 1645
[1] "eps= 1.5"

   0    1
 285 1715 

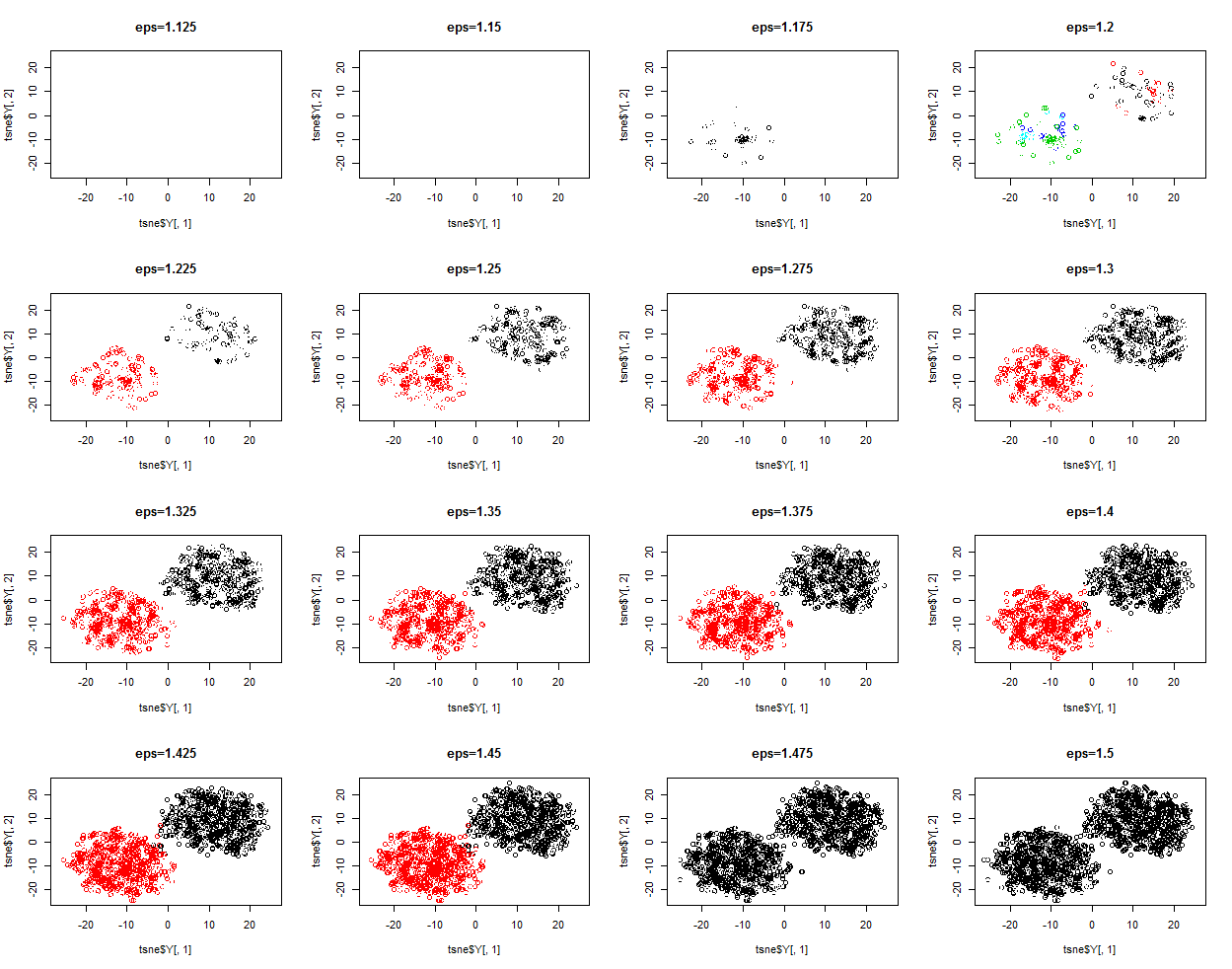
可以看出，DBSCAN虽然性能优越，但是涉及到有些麻烦的调参数的过程，需要进行很多次的试探，没有K-means和K-medoids来的方便快捷。

Python

在Python中，DBSCAN算法集成在sklearn.cluster中，我们利用datasets构造两个非凸集和一个凸集，效果如下：

from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import style
from sklearn.cluster import KMeans,DBSCAN

style.use('ggplot')
'''构造样本集'''
X1, y1=datasets.make_circles(n_samples=5000, factor=.6,noise=.05)
X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[1.2,1.2]], cluster_std=[[.1]],random_state=9)

X = np.concatenate((X1, X2))
plt.scatter(X[:, 0], X[:, 1], marker='*')
plt.title('Samples')

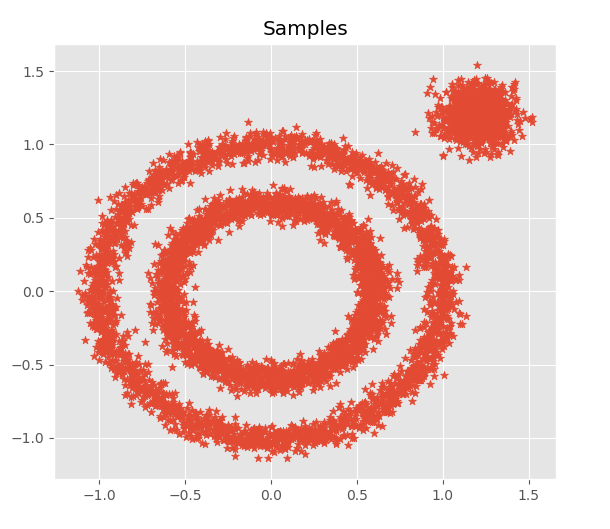
分别使用K-means和DBSCAN对上述样本集进行聚类，效果如下:

'''利用K-means'''
km = KMeans(n_clusters=3).fit_predict(X)
col = [(['red','green','blue','yellow','grey','purple'])[i] for i in km]

plt.figure(figsize=(16,8))
plt.subplot(121)
plt.scatter(X[:, 0], X[:, 1], marker='*',c=col)
plt.title('K-means')

'''利用DBSCAN'''
db = DBSCAN(eps = 0.12, min_samples = 19).fit_predict(X)
col = [(['red','green','blue','yellow'])[i] for i in db]
plt.subplot(122)
plt.scatter(X[:, 0], X[:, 1], marker='*',c=col)
plt.title('DBSCAN')

对DBSCAN中的参数eps（超球体半径）进行试探：

'''对eps进行试探性调整'''
plt.figure(figsize=(15,15))
for i in range(9):
    db = DBSCAN(eps = 0.05+i*0.04, min_samples = 19).fit_predict(X)
    col = [(['red','green','blue','yellow','purple','aliceblue','antiquewhite','black','blueviolet','cyan','darkgray'])[i] for i in db]
    plt.subplot(331+i)
    plt.scatter(X[:, 0], X[:, 1], marker='*',c=col)
    plt.title('eps={}'.format(str(round(0.05+i*0.04,2))))

对DBSCAN中的参数MinPts（核心点内最少样本个数）进行试探：

'''对MinPts进行试探性调整'''
plt.figure(figsize=(15,15))
for i in range(9):
    db = DBSCAN(eps = 0.12, min_samples = 10+i*4).fit_predict(X)
    col = [(['red','green','blue','yellow','purple','aliceblue','antiquewhite','black','blueviolet','cyan','darkgray'])[i] for i in db]
    plt.subplot(331+i)
    plt.scatter(X[:, 0], X[:, 1], marker='*',c=col)
    plt.title('MinPts={}'.format(str(round(10+i*4))))

可见参数的设置对聚类效果的影响非常显著。

以上就是DBSCAN的简单介绍，若发现错误望指出。