LeetCode 1259. Handshakes That Don't Cross - Java - DP

题目链接：https://leetcode-cn.com/problems/handshakes-that-dont-cross/

---

You are given an even number of people num_people that stand around a circle and each person shakes hands with someone else, so that there are num_people / 2 handshakes total.

Return the number of ways these handshakes could occur such that none of the handshakes cross.

Since this number could be very big, return the answer mod 10^9 + 7

Example 1:

Input: num_people = 2
Output: 1

Example 2:

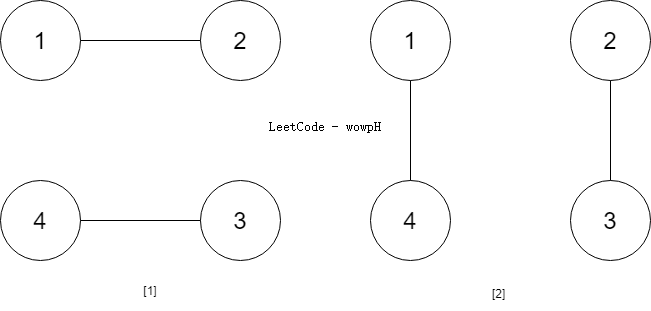
Input: num_people = 4
Output: 2
Explanation: There are two ways to do it, the first way is [(1,2),(3,4)] and the second one is [(2,3),(4,1)].

Example 3:

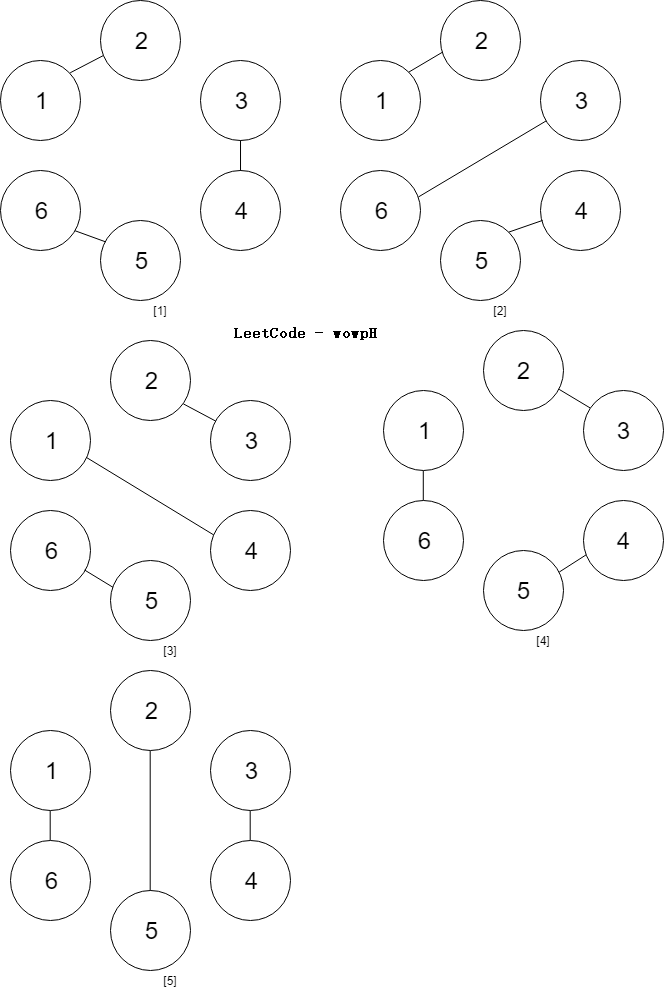
Input: num_people = 6
Output: 5

Example 4:

Input: num_people = 8
Output: 14

Constraints:

• 2 <= num_people <= 1000
• num_people % 2 == 0

---

题解

先分析一下示例 3，

第 6 个人和第 5 个人握手，圆被分成两部分，一部分是 4 个人，另一部分是 0 个人。0 个人的方案数为 1，4 个人的方案数可以递归计算为 2，所以这种情况有 2 种方案。

第 6 个人和第 3 个人握手，圆被分成两部分，每部分都是 2 个人，2 个人的方案数是 1，所以这种情况有 1 种方案。

第 6 个人和第 1 个人握手，圆被分成两部分，一部分是 0 个人，另一部分是 4 个人，所以这种情况有 2 中方案。

因此 6 个人的时候有 5 种方案数。@wowpH

有 n 个人（n为偶数），如果第 n 个人和第 i （i = n - 1, n - 3, ……，1）个人握手，那么分成的两部分中，一部分有 i - 1 人，另一部分有 n - i - 1 人。这两部分又是一个新的子问题。

所以题目可以采用 动态规划(DP) 来解决。

用大小为 num_people + 1 的 long 型一维数组 arr 来保存每种人数时的方案数。公式为：

\[arr[n] = \begin{cases}
1 &\text{ } n=0或n=2 \\
\displaystyle\sum_{i=1}^{n-1} (arr[i - 1] * arr[n - i - 1]) &\text{ } n>2，n为偶数，i为奇数
\end{cases}.\]

---

Java代码

/**
 * @description 5125. Handshakes That Don't Cross
 * @time 10ms
 * @version 1.1
 * @author wowpH
 * @date 2019-11-17 22:44:21
 */
class Solution {
    private static final int mod = 1000000007;
    private long[] arr;

    public int numberOfWays(int num_people) {
        arr = new long[num_people + 1];
        return (int) dp(num_people);
    }

    private long dp(int n) {
        if (n == 0 || n == 2) {
            return 1;
        }
        long ret = 0;
        for (int i = n - 1; i >= 1; i -= 2) {
            if (arr[i - 1] == 0) {
                arr[i - 1] = dp(i - 1);
            }
            if (arr[n - i - 1] == 0) {
                arr[n - i - 1] = dp(n - i - 1);
            }
            ret += arr[i - 1] * arr[n - i - 1];
            ret %= mod;
        }
        return ret;
    }
}

---

原文链接：https://www.cnblogs.com/wowpH/p/11880952.html

---

- wowpH -