Union-Find 并查集算法

一、动态连通性(Dynamic Connectivity）

Union-Find 算法（中文称并查集算法）是解决动态连通性（Dynamic Conectivity）问题的一种算法。动态连通性是计算机图论中的一种数据结构，动态维护图结构中相连信息。简单的说就是，图中各个节点之间是否相连、如何将两个节点连接，连接后还剩多少个连通分量。有点像我们的微信朋友圈，在社交网络中，彼此熟悉的人之间组成自己的圈子，熟悉之后就会添加好友，加入新的圈子。微信用户有几亿人，如何快速计算任意两个用户是否同属于一个圈子呢？计算机是如何将两个用户连接起来的呢？整个微信用户共有几个独立的圈子呢？Union-Find就可以解决上述问题。

二、基本概念
结合下面图的例子来了解基本概念：

 

图中8个节点都是独立互不连通的，也就是一共有8个连通分量。

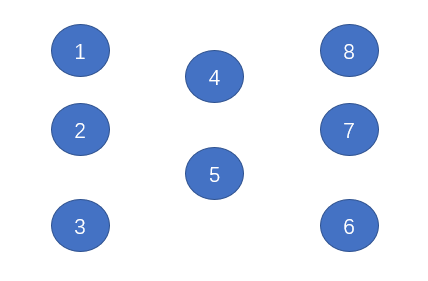
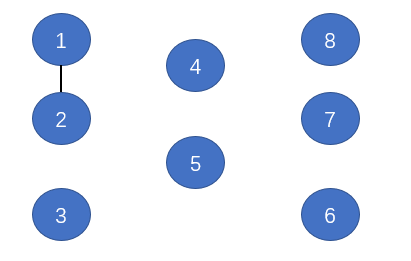
连通是一种等价关系，也就是说具有如下三个性质：

1、自反性：节点p和p是连通的。

2、对称性：如果节点p和q连通，那么q和p也连通。

3、传递性：如果节点p和q连通，q和r连通，那么p和r也连通。

如果将节点1和节点2进行连接，那连通分量就剩余7个，如下图：

如何在计算中实现这些操作呢？

 

class UF:
　　 def __init__(self,N): #N表示初始化的节点数，也即最初的连通分量数
    def union(self,p,q): # 将节点p和q进行连接
    def connected(self,p,q): #判断p和q是否连接
    def count(): #返回当前的连通分量

除了社交网络中的朋友圈计算，还可以判断编译器同一个变量的不同引用。

Union-Find 算法的关键就在于union和connected函数的效率。使用什么样的数据结构来实现这种高效率呢？

三、解决思路

用树来表示节点直接的连接，只要是连接的节点都在同一颗树中，多棵树就是多个连通分量，进而组成了整个森林。怎么用森林来表示连通性呢？我们设定树的每个节点都有一个指针指向其父节点，如果是根节点的话，这个指针指向自己。

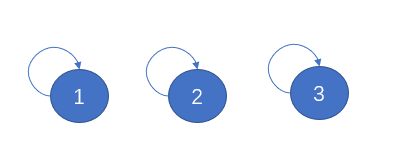
如果某两个节点被连通，则让其中的（任意）一个节点的根节点接到另一个节点的根节点上，这样，如果节点p和q连通的话，它们一定拥有相同的根节点：

class UF:
    def __init__(self,N): #N表示初始化的节点数，也即最初的连通分量数
        self.count=N
        self.root=[0] #root表示存储每个节点的根节点，第一个位置用0占位
        for i in range(1,N+1): #初始化每个节点的根节点指向自己
            self.root.append(i)

    def union(self,p,q):  # 将节点p和q进行连接，让p的根节点指向q节点的根节点即可
        if self.connected(p,q):
            return;
        p_root=self.find(p)
        q_root=self.find(q)
        self.root[p_root]=q_root
        self.count-=1

    def find(self,p):     #查找节点p的根节点
        while p!=self.root[p]:
            p=self.root[p]
        return p

    def connected(self,p,q): #判断p和q是否连接
        return self.find(p)=self.find(q)

    def count(): #返回当前的连通分量
        return self.count

 算法效率分析：

从上述代码可以看出，union-find算法的效率主要在于find函数上面，因为union和connected两个函数的关键都在查找根节点上面，即find函数。find主要功能就是从某个节点向上遍历到树根，其时间复杂度就是树的高度。我们可能习惯性地认为树的高度就是logN，但这并不一定。logN的高度只存在于平衡二叉树，对于一般的树可能出现极端不平衡的情况，使得树几乎退化成直线链表，树的高度最坏情况下可能变成N，如下图所示:

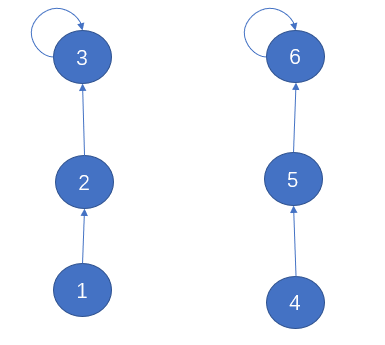
如果按照上面的情况，左边圈子与右边圈子进行连接的话，每个圈子找到根节点的时间复杂度都是O(N)级别的，对于诸如社交网络这样数据规模巨大的问题，而union和connected的调用都非常频繁，每次都需要线性时间复杂度，效率就显得比较低下了。其实这个问题就是树不平衡造成的。

四、平衡树

 造成树不平衡的主要原因就是在节点关联的时候，没有考虑树节点的多少，而是直接将p节点的根节点直接关联到q节点的根节点上。

 

如上图所示，第一种关联就是不平衡树，第二种关联就比较好。所以改进的方法就是，在union之前，先判断两个树的大小（节点数量），将小点的树附加到大点的树上。这样，合并后的树的深度不会变得非常大。要判断树的大小，需要引进一个新的数组，size 数组，存放树的大小，初始化的时候 size 各元素都设为 1。

class UF:
    def __init__(self,N): #N表示初始化的节点数，也即最初的连通分量数
        self.count=N
        self.root=[0] #root表示存储每个节点的根节点，第一个位置用0占位
        self.size=[0]
        for i in range(1,N+1): #初始化每个节点的根节点指向自己,树的大小为1
            self.root.append(i)
            self.size.append(1)

    def union(self,p,q):  # 将节点p和q进行连接，让p的根节点指向q节点的根节点即可
        if self.connected(p,q):
            return;
        p_root=self.find(p)
        q_root=self.find(q)
        if size[p_root]<= size[q_root]:
            self.root[p_root]=q_root
            self.size[q_root]+=self.size[p_root] #p节点数合并到q根节点上
        else:
            self.root[q_root]=self.root[p_root]
            self.size[p_root]=self.size[p_root] #q节点数合并到p根节点上
        self.count-=1

    def find(self,p):     #查找节点p的根节点
        while p!=self.root[p]:
            p=self.root[p]
        return p

    def connected(self,p,q): #判断p和q是否连接
        return self.find(p)=self.find(q)

    def count(): #返回当前的连通分量
        return self.count

 

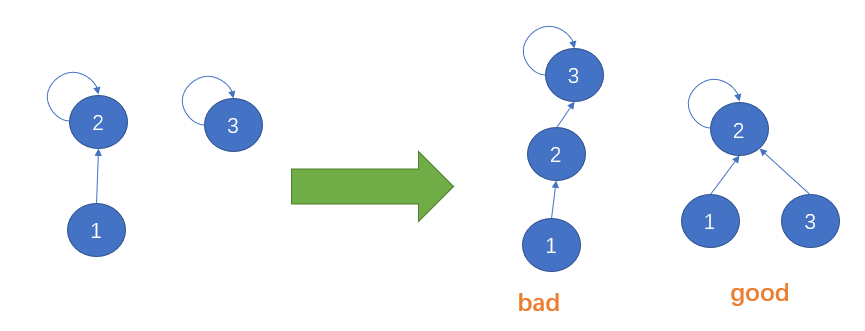
五、路径压缩(进一步优化find函数)

是不是可以进一步压缩树的高度，加快find函数的查找速度，find的效率提升了，等于union和connected函数效率提升了。

如果是上图这种形式，那查找速度基本就是O(1)级别了。但是一个平衡树一步是不可能压缩到这种形式，可以在find函数中加上一行代码，在每次查找的时候，就可以顺便压缩了路径，将树的高度进一步降低，代码如下：

class UF:
    def __init__(self,N): #N表示初始化的节点数，也即最初的连通分量数
        self.count=N
        self.root=[0] #root表示存储每个节点的根节点，第一个位置用0占位
        self.size=[0]
        for i in range(1,N+1): #初始化每个节点的根节点指向自己,树的大小为1
            self.root.append(i)
            self.size.append(1)

    def union(self,p,q):  # 将节点p和q进行连接，让p的根节点指向q节点的根节点即可
        p_root=self.find(p)
        q_root=self.find(q)
        if p_root==q_root:
            return
        if self.size[p_root]<= self.size[q_root]:
            self.root[p_root]=q_root
            self.size[q_root]+=self.size[p_root] #p节点数合并到q根节点上
        else:
            self.root[q_root]=self.root[p_root]
            self.size[p_root]=self.size[p_root] #q节点数合并到p根节点上
        self.count-=1

    def find(self,p):     #查找节点p的根节点
        while p!=self.root[p]:
            self.root[p]=self.root[self.root[p]]#路径压缩，直接把p节点指向其父节点的父节点，其实查找也变成了跳跃查找了。
            p=self.root[p]
        return p

    def connected(self,p,q): #判断p和q是否连接
        return self.find(p)==self.find(q)

    def count_func(): #返回当前的连通分量
        return self.count

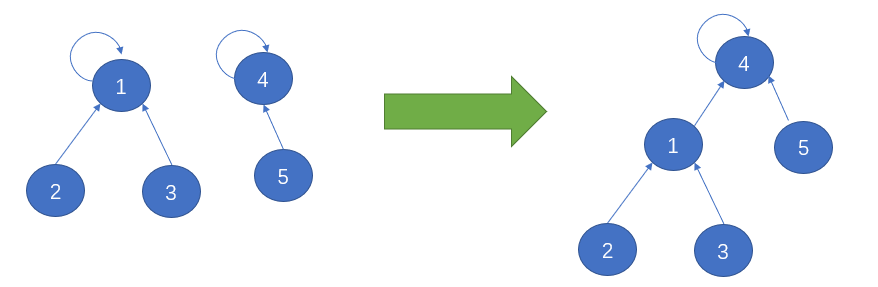
这种思路每调用一次find函数，路径就会压缩一次，直到路径不能压缩为止。

看代码不好理解，我们以图示的形式进行展示：

 

可以看出每查找一次跟节点，路径就压缩一次。