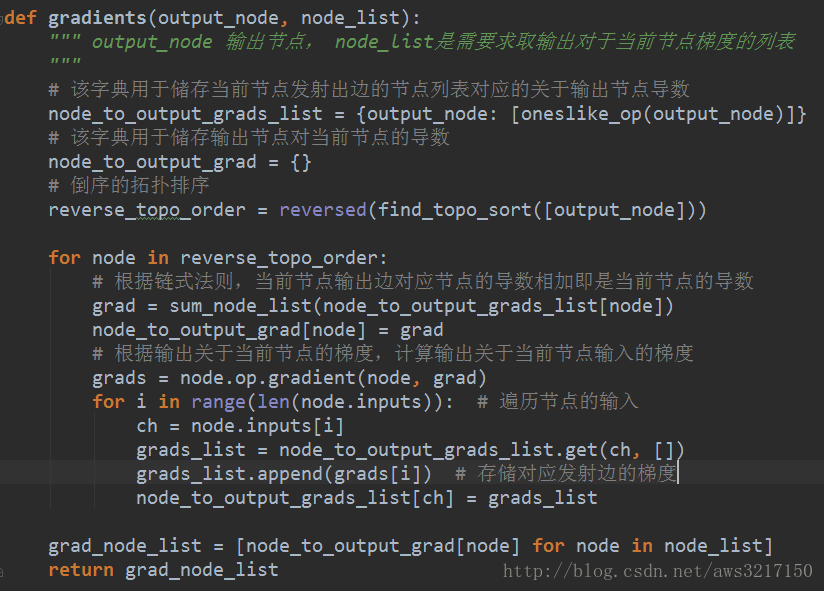
（转）自动微分(Automatic Differentiation)简介——tensorflow核心原理

现代深度学习系统中（比如MXNet， TensorFlow等）都用到了一种技术——自动微分。在此之前，机器学习社区中很少发挥这个利器，一般都是用Backpropagation进行梯度求解，然后进行SGD等进行优化更新。手动实现过backprop算法的同学应该可以体会到其中的复杂性和易错性，一个好的框架应该可以很好地将这部分难点隐藏于用户视角，而自动微分技术恰好可以优雅解决这个问题。接下来我们将一起学习这个优雅的技术:-)。本文主要来源于陈天奇在华盛顿任教的课程CSE599G1: Deep Learning System和《Automatic differentiation in machine learning: a survey》。

什么是自动微分

微分求解大致可以分为4种方式：

• 手动求解法(Manual Differentiation)
• 数值微分法(Numerical Differentiation)
• 符号微分法(Symbolic Differentiation)
• 自动微分法(Automatic Differentiation)

为了讲明白什么是自动微分，我们有必要了解其他方法，做到有区分有对比，从而更加深入理解自动微分技术。

手动求解法

手动求解其实就对应我们传统的backprop算法，我们求解出梯度公式，然后编写代码，代入实际数值，得出真实的梯度。在这样的方式下，每一次我们修改算法模型，都要修改对应的梯度求解算法，因此没有很好的办法解脱用户手动编写梯度求解的代码，这也是为什么我们需要自动微分技术的原因。

数值微分法

数值微分法是根据导数的原始定义：

f′(x)=limh→0f(x+h)−f(x)hf′(x)=limh→0f(x+h)−f(x)h

那么只要hh取很小的数值，比如0.0001，那么我们可以很方便求解导数，并且可以对用户隐藏求解过程，用户只要给出目标函数和要求解的梯度的变量，程序可以自动给出相应的梯度，这也是某种意义上的“自动微分”:-)。不幸的是，数值微分法计算量太大，求解速度是这四种方法中最慢的，更加雪上加霜的是，它引起的roundoff error和truncation error使其更加不具备实际应用场景，为了弥补缺点，便有如下center difference approximation：

f′(x)=limh→0f(x+h)−f(x−h)2hf′(x)=limh→0f(x+h)−f(x−h)2h

可惜并不能完全消除truncation error，只是将误差减小。虽然数值微分法有如上缺点，但是由于它实在是太简单实现了，于是很多时候，我们利用它来检验其他算法的正确性，比如在实现backprop的时候，我们用的”gradient check”就是利用数值微分法。

符号微分法

符号微分是代替我们第一种手动求解法的过程，利用代数软件，实现微分的一些公式比如：

ddx(f(x)+g(x))=ddxf(x)+ddxg(x)ddxf(x)g(x)=(ddxf(x))g(x)+f(x)(ddxg(x))ddxf(x)g(x)=f′(x)g(x)−f(x)g′(x)g(x)2ddx(f(x)+g(x))=ddxf(x)+ddxg(x)ddxf(x)g(x)=(ddxf(x))g(x)+f(x)(ddxg(x))ddxf(x)g(x)=f′(x)g(x)−f(x)g′(x)g(x)2

然后对用户提供的具有closed form的数学表达式进行“自动微分”求解，什么是具有closed form的呢？也就是必须能写成完整数学表达式的，不能有编程语言中的循环结构，条件结构等。因此如果能将问题转化为一个纯数学符号问题，我们能利用现有的代数软件进行符号微分求解，这种程度意义上的“自动微分”其实已经很完美了。然而缺点我们刚刚也提及过了，就是必须要有closed form的数学表达式，另一个有名的缺点是“表达式膨胀”（expression swell）问题，如果不加小心就会使得问题符号微分求解的表达式急速“膨胀”，导致最终求解速度变慢，对于这个问题请看如下图： 

稍不注意，符号微分求解就会如上中间列所示，表达式急剧膨胀，导致问题求解也随着变慢。

自动微分法

终于轮到我们的主角登场，自动微分的存在依赖于它识破如下事实：

所有数值计算归根结底是一系列有限的可微算子的组合

自动微分法是一种介于符号微分和数值微分的方法：数值微分强调一开始直接代入数值近似求解；符号微分强调直接对代数进行求解，最后才代入问题数值；自动微分将符号微分法应用于最基本的算子，比如常数，幂函数，指数函数，对数函数，三角函数等，然后代入数值，保留中间结果，最后再应用于整个函数。因此它应用相当灵活，可以做到完全向用户隐藏微分求解过程，由于它只对基本函数或常数运用符号微分法则，所以它可以灵活结合编程语言的循环结构，条件结构等，使用自动微分和不使用自动微分对代码总体改动非常小，并且由于它的计算实际是一种图计算，可以对其做很多优化，这也是为什么该方法在现代深度学习系统中得以广泛应用。

自动微分Forward Mode

考察如下函数：

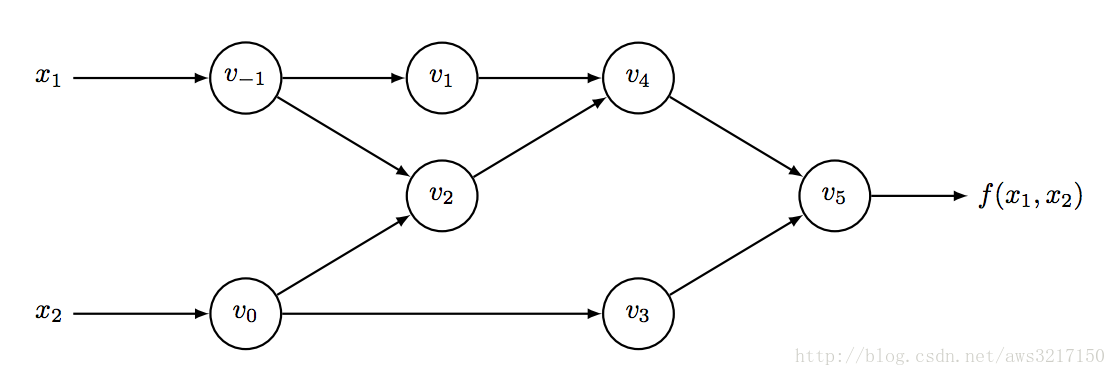
f(x1,x2)=ln(x1)+x1x2−sin(x2)f(x1,x2)=ln(x1)+x1x2−sin(x2)

我们可以将其转化为如下计算图： 

转化成如上DAG（有向无环图）结构之后，我们可以很容易分步计算函数的值，并求取它每一步的导数值： 

上表中左半部分是从左往右每个图节点的求值结果，右半部分是每个节点对于x1x1的求导结果，比如v1˙=dvdx1v1˙=dvdx1，注意到每一步的求导都利用到上一步的求导结果，这样不至于重复计算，因此也不会产生像符号微分法的”expression swell”问题。 
自动微分的forward mode非常符合我们高数里面学习的求导过程，只要您对求导法则还有印象，理解forward mode自不在话下。如果函数输入输出为：

R→RmR→Rm

那么利用forward mode只需计算一次如上表右边过程即可，非常高效。对于输入输出映射为如下的：

Rn→RmRn→Rm

这样一个有nn个输入的函数，求解函数梯度需要nn遍如上计算过程。然而实际算法模型中，比如神经网络，通常输入输出是极其不成比例的，也就是：

n>>mn>>m

那么利用forward mode进行自动微分就太低效了，因此便有下面要介绍的reverse mode。

自动微分Reverse Mode

如果您理解神经网络的backprop算法，那么恭喜你，自动微分的backward mode其实就是一种通用的backprop算法，也就是backprop是reverse mode自动微分的一种特殊形式。从名字可以看出，reverse mode和forward mode是一对相反过程，reverse mode从最终结果开始求导，利用最终输出对每一个节点进行求导，其过程如下红色箭头所示：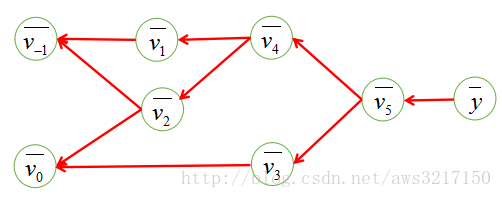 
 
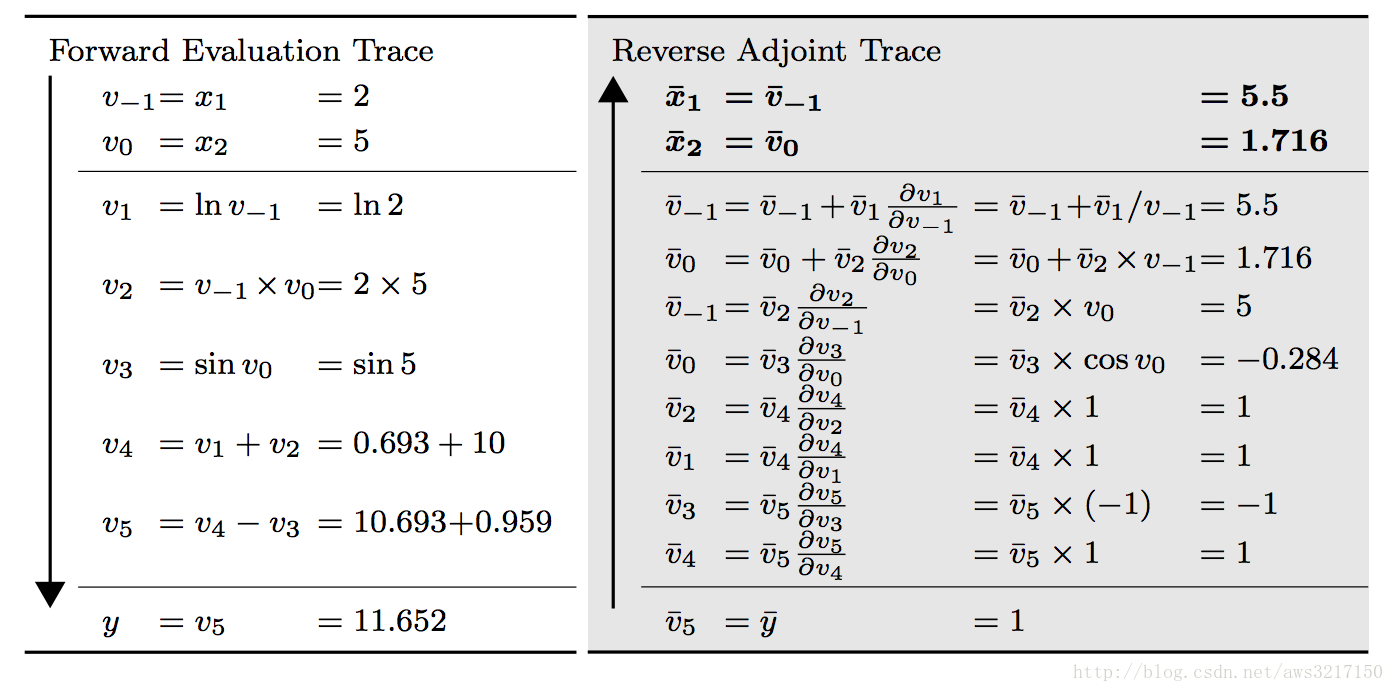
其具体计算过程如下表所示： 

上表左边和之前的forward mode一致，用于求解函数值，右边则是reverse mode的计算过程，注意必须从下网上看，也就是一开始先计算输出yy对于节点v5v5的导数，用v¯¯¯5v¯5表示dydv5dydv5，这样的记号可以强调我们对当前计算结果进行缓存，以便用于后续计算，而不必重复计算。由链式法则我们可以计算输出对于每个节点的导数。 
比如对于节点v3v3:

dydv3=dydv5dv5dv3dydv3=dydv5dv5dv3

用另一种记法变得到：

dydv3=v5¯¯¯¯¯dv5dv3dydv3=v5¯dv5dv3

比如对于节点v0v0：

dydv0=dydv2dv2dv0+dydv3dv3dv0dydv0=dydv2dv2dv0+dydv3dv3dv0

如果用另一种记法，便可得出：

dydv0=v¯¯¯2dv2dv0+v¯¯¯3dv3dv0dydv0=v¯2dv2dv0+v¯3dv3dv0

和backprop算法一样，我们必须记住前向时当前节点发出的边，然后在后向传播的时候，可以搜集所有受到当前节点影响节点。 
如上的计算过程，对于像神经网络这种模型，通常输入是上万到上百万维，而输出损失函数是1维的模型，只需要一遍reverse mode的计算过程，便可以求出输出对于各个输入的导数，从而轻松求取梯度用于后续优化更新。

自动微分的实现

这里主要讲解reverse mode的实现方式，forward mode的实现基本和reverse mode一致，但是由于机器学习算法中大部分用reverse mode才可以高效求解，所以它是我们理解的重心。代码设计轮廓来源于CSE599G1的作业，通过分析完成作业，可以展示自动微分的简洁性和灵活可用性。 
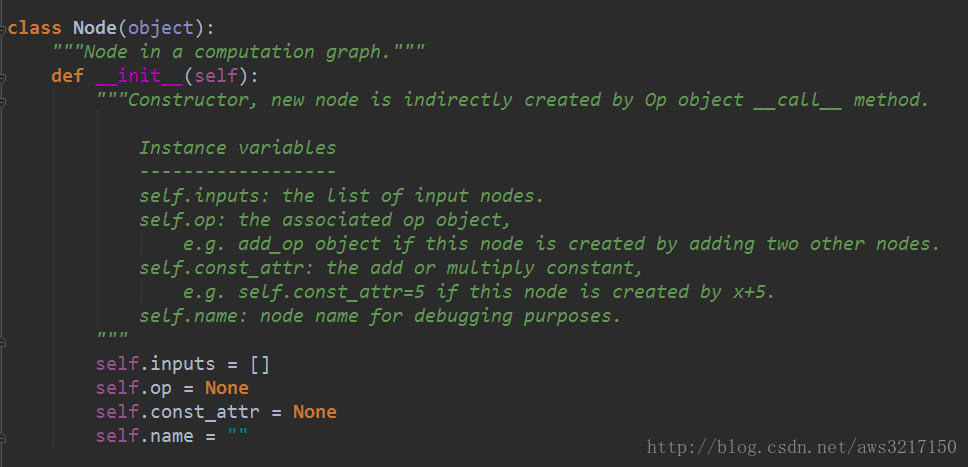
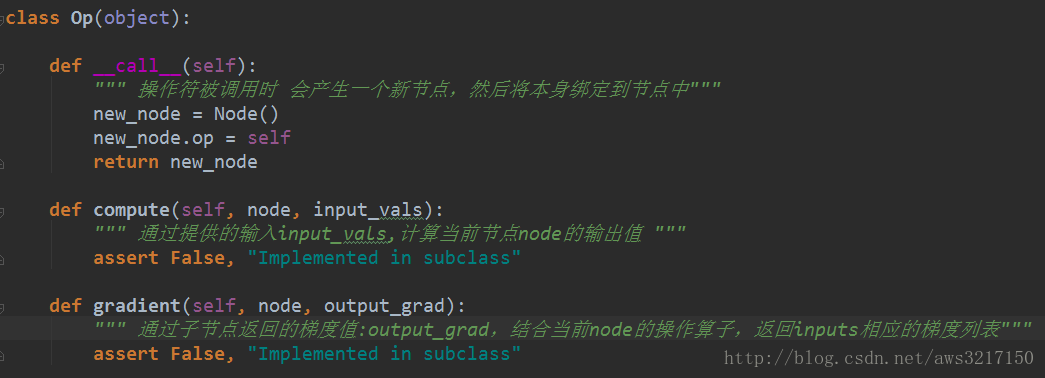
首先自动微分会将问题转化成一种有向无环图，因此我们必须构造基本的图部件，包括节点和边。可以先看看节点是如何实现的： 

首先节点可以分为三种：

• 常数节点
• 变量节点
• 带操作算子节点

因此Node类中定义了op成员用于存储节点的操作算子，const_attr代表节点的常数值，name是节点的标识，主要用于调试。 
对于边的实现则简单的多，每个节点只要知道本身的输入节点即可，因此用inputs来描述节点的关系。 
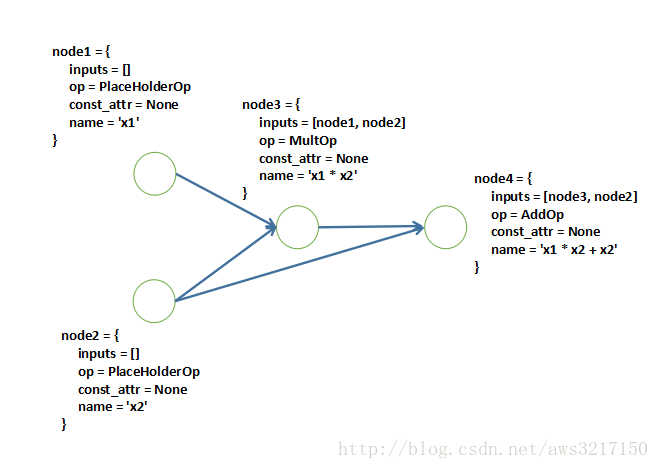
有了如上的定义，利用操作符重载，我们可以很简单构造一个计算图，举一个简单的例子：

f(x1,x2)=x1x2+x2f(x1,x2)=x1x2+x2

对于如上函数，只要重载加法和乘法操作符，我们可以轻松得到如下计算图： 

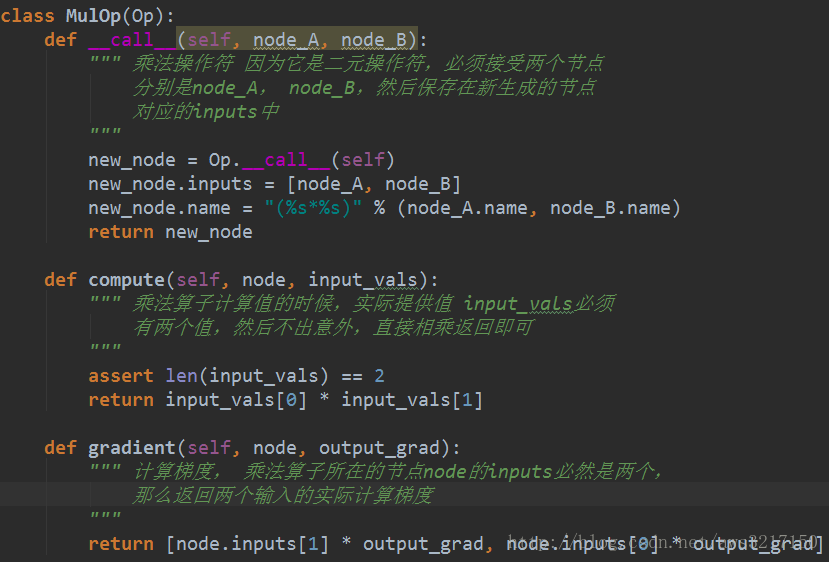
操作算子是自动微分最重要的组成部分，接下来我们重点介绍，先上代码： 

从定义可以看出，所有实际计算都落在各个操作算子中，上面代码应该抽象一些，我们来举一个乘法算子的例子加以说明： 

我们重点讲解一下gradient方法，它接收两个参数，一个是node，也就是当前要计算的节点，而output_grad则是后面节点传来的，我们来看看它到底是啥玩意，对于如下例子：

y=f(x1∗x2)y=f(x1∗x2)

那么要求yy关于x1x1的导数，那么根据链式法则可得：

∂y∂x1=∂y∂f∂f∂x1=∂y∂x1x2∂x1x2∂x1=output_grad∗x2∂y∂x1=∂y∂f∂f∂x1=∂y∂x1x2∂x1x2∂x1=output_grad∗x2

则output_grad就是上面的∂y∂f∂y∂f，计算yy对于x2x2类似。因此在程序中我们会返回如下：

return [node.inputs[1] * output_grad, node.inputs[0] * output_grad]

• 1

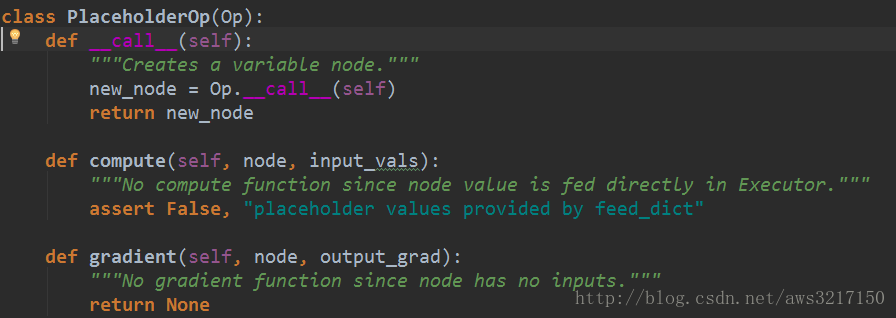
再来介绍一个特殊的op——PlaceHolderOp，它的作用就如同名字，起到占位符的作用，也就是自动微分中的变量，它不会参与实际计算，只等待用户给他提供实际值，因此他的实现如下： 

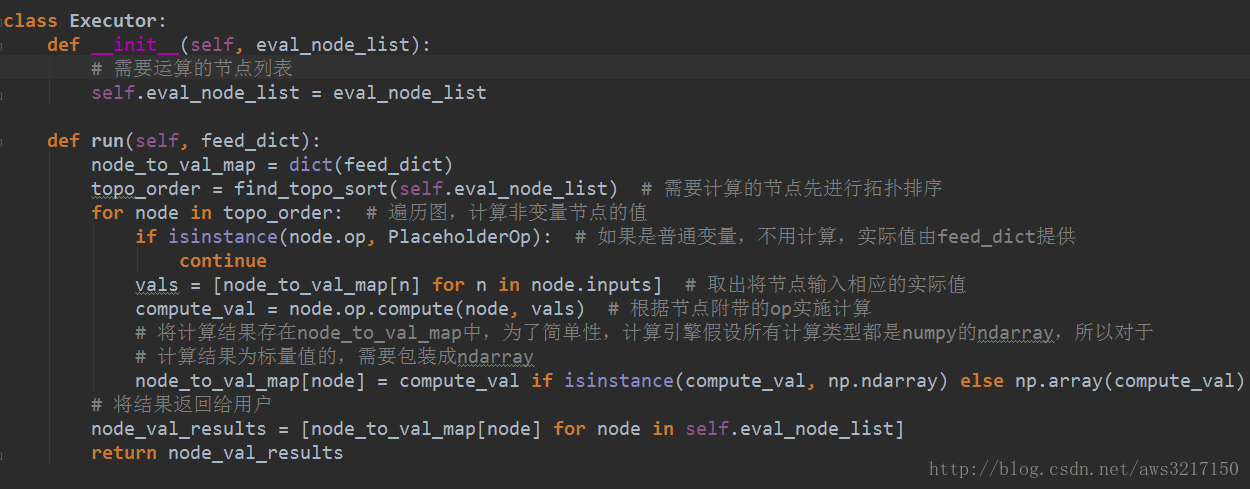
了解了节点和操作算子的定义，接下来我们考虑如何协调执行运算。首先是如何计算函数值，对于一幅计算图，由于节点与节点之间的计算有一定的依赖关系，比如必须先计算node1之后才可以计算node2，那么如何能正确处理好计算关系呢？一个简单的方式是对图节点进行拓扑排序，这样可以保证需要先计算的节点先得到计算。这部分代码由Executor掌控： 

Executor是实际计算图的引擎，用户提供需要计算的图和实际输入，Executor计算相应的值和梯度。

如何从计算图中计算函数的值，上面我们已经介绍了，接下来是如何自动计算梯度。reverse mode的自动微分，要求从输出到输入节点，按照先后依赖关系，对各个节点求取输出对于当前节点的梯度，那么和我们上面介绍的刚好相反，为了得到正确计算节点顺序，我们可以将图节点的拓扑排序倒序即可。代码也很简单，如下所示： 

这里先介绍一个新的算子——oneslike_op。他是一个和numpy自带的oneslike函数一样的算子，作用是构造reverse梯度图的起点，因为最终输出关于本身的梯度就是一个和输出shape一样的全1数组，引入oneslike_op可以使得真实计算得以延后，因此gradients方法最终返回的不是真实的梯度，而是梯度计算图，然后可以复用Executor，计算实际的梯度值。 
紧接着是根据输出节点，获得倒序的拓扑排序序列，然后遍历序列，构造实际的梯度计算图。我们重点来介绍node_to_output_grad和node_to_output_grads_list这两个字典的意义。 
先关注node_to_output_grads_list，他key是节点，value是一个梯度列表，代表什么含义呢？先看如下部分计算图：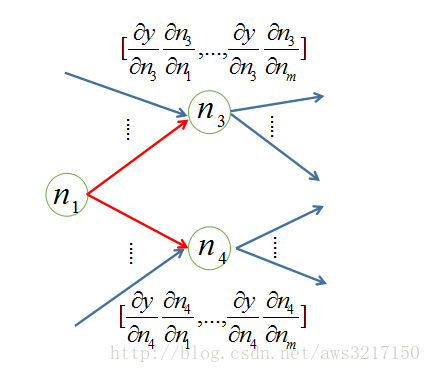 
 
此时我们要计算输出yy关于节点n1n1的导数，那么我们观察到他的发射边连接的节点有n3,n4n3,n4，而对应n3,n4n3,n4节点调用相应op的gradient方法，会返回输出yy关于各个输入节点的导数。此时为了准确计算输出yy关于节点n1n1的导数，我们需要将其发射边关联节点的计算梯度搜集起来，比如上面的例子，我们需要搜集：

node_to_output_grads_list={n1:[∂y∂n3∂n3∂n1,∂y∂n4∂n4∂n1]}node_to_output_grads_list={n1:[∂y∂n3∂n3∂n1,∂y∂n4∂n4∂n1]}

一旦搜集好对应输出边节点关于当前节点导数，那么当前节点的导数便可以由链式法则计算得出，也就是：

∂y∂n1=∂y∂n3∂n3∂n1+∂y∂n4∂n4∂n1∂y∂n1=∂y∂n3∂n3∂n1+∂y∂n4∂n4∂n1

因此node_to_output_grad字典存储的就是节点对应的输出关于节点的导数。经过gradients函数执行后，会返回需要求取输出关于某节点的梯度计算图： 
 
而对于Executor而言，它并不知道此时的图是否被反转，它只关注用户实际输入，还有计算相应的值而已。

自动梯度的应用

有了上面的大篇幅介绍，我们其实已经实现了一个简单的自动微分引擎了，接下来看如何使用： 

使用相当简单，我们像编写普通程序一样，对变量进行各种操作，只要提供要求导数的变量，还有提供实际输入，引擎可以正确给出相应的梯度值。 
下面给出一个根据自动微分训练Logistic Regression的例子：

1.  
   import autodiff as ad
2.  
   import numpy as np
3.  
    
4.  
    
5.  
   def logistic_prob(_w):
6.  
   def wrapper(_x):
7.  
   return 1 / (1 + np.exp(-np.sum(_x * _w)))
8.  
   return wrapper
9.  
    
10.  
     
11.  
    def test_accuracy(_w, _X, _Y):
12.  
    prob = logistic_prob(_w)
13.  
    correct = 0
14.  
    total = len(_Y)
15.  
    for i in range(len(_Y)):
16.  
    x = _X[i]
17.  
    y = _Y[i]
18.  
    p = prob(x)
19.  
    if p >= 0.5 and y == 1.0:
20.  
    correct += 1
21.  
    elif p < 0.5 and y == 0.0:
22.  
    correct += 1
23.  
    print("总数：%d, 预测正确：%d" % (total, correct))
24.  
     
25.  
     
26.  
    def plot(N, X_val, Y_val, w, with_boundary=False):
27.  
    import matplotlib.pyplot as plt
28.  
    for i in range(N):
29.  
    __x = X_val[i]
30.  
    if Y_val[i] == 1:
31.  
    plt.plot(__x[1], __x[2], marker='x')
32.  
    else:
33.  
    plt.plot(__x[1], __x[2], marker='o')
34.  
    if with_boundary:
35.  
    min_x1 = min(X_val[:, 1])
36.  
    max_x1 = max(X_val[:, 1])
37.  
    min_x2 = float(-w[0] - w[1] * min_x1) / w[2]
38.  
    max_x2 = float(-w[0] - w[1] * max_x1) / w[2]
39.  
    plt.plot([min_x1, max_x1], [min_x2, max_x2], '-r')
40.  
     
41.  
    plt.show()
42.  
     
43.  
     
44.  
    def gen_2d_data(n):
45.  
    x_data = np.random.random([n, 2])
46.  
    y_data = np.ones(n)
47.  
    for i in range(n):
48.  
    d = x_data[i]
49.  
    if d[0] + d[1] < 1:
50.  
    y_data[i] = 0
51.  
    x_data_with_bias = np.ones([n, 3])
52.  
    x_data_with_bias[:, 1:] = x_data
53.  
    return x_data_with_bias, y_data
54.  
     
55.  
     
56.  
    def auto_diff_lr():
57.  
    x = ad.Variable(name='x')
58.  
    w = ad.Variable(name='w')
59.  
    y = ad.Variable(name='y')
60.  
     
61.  
    # 注意，以下实现某些情况会有很大的数值误差，
62.  
    # 所以一般真实系统实现会提供高阶算子，从而减少数值误差
63.  
     
64.  
    h = 1 / (1 + ad.exp(-ad.reduce_sum(w * x)))
65.  
    L = y * ad.log(h) + (1 - y) * ad.log(1 - h)
66.  
    w_grad, = ad.gradients(L, [w])
67.  
    executor = ad.Executor([L, w_grad])
68.  
     
69.  
    N = 100
70.  
    X_val, Y_val = gen_2d_data(N)
71.  
    w_val = np.ones(3)
72.  
     
73.  
    plot(N, X_val, Y_val, w_val)
74.  
    executor = ad.Executor([L, w_grad])
75.  
    test_accuracy(w_val, X_val, Y_val)
76.  
    alpha = 0.01
77.  
    max_iters = 300
78.  
    for iteration in range(max_iters):
79.  
    acc_L_val = 0
80.  
    for i in range(N):
81.  
    x_val = X_val[i]
82.  
    y_val = np.array(Y_val[i])
83.  
    L_val, w_grad_val = executor.run(feed_dict={w: w_val, x: x_val, y: y_val})
84.  
    w_val += alpha * w_grad_val
85.  
    acc_L_val += L_val
86.  
    print("iter = %d, likelihood = %s, w = %s" % (iteration, acc_L_val, w_val))
87.  
    test_accuracy(w_val, X_val, Y_val)
88.  
    plot(N, X_val, Y_val, w_val, True)
89.  
     
90.  
     
91.  
    if __name__ == '__main__':
92.  
    auto_diff_lr()

• 转载：https://blog.csdn.net/aws3217150/article/details/70214422