BZOJ1010_玩具装箱toy_KEY

题目传送门

这道题可以很快想到暴力DP的做法：

f[i]=min(f[i],f[j]+(C[i]-C[j]+i-j--L)^);

但是数据范围有50000，这就需要用斜率优化了。

我们设S[i]=C[i]+i(C[i]为前缀和)，L++,设j为i的最优决策点。。

原方程就变为：

f[i]=f[j]+(S[i]-(S[j]-L))^;
f[i]=f[j]+S[i]^2+(S[j]-L)^2-2*S[i]*(S[j]-L);
f[j]+S[i]^2+(S[j]-L)^2=2*S[i]*(S[j]-L)+f[i];
        y             =  k        x   + b

我们设2*S[i]为k。

相当于这题就变成了求最小的截距f[i]。

假设A，B，C，D为四个决策点。

因为AB的斜率小于f的斜率(2*S[i])，所以它对当前状态的转移一定是没用的。

因为如果要进过A点转移，需要将f"抬高"很多，会大大增大它的截距(f[i])。

所以斜率小于f(当前点)都可以排除。

所以B为最优决策点。

通过B点转移后，如图：

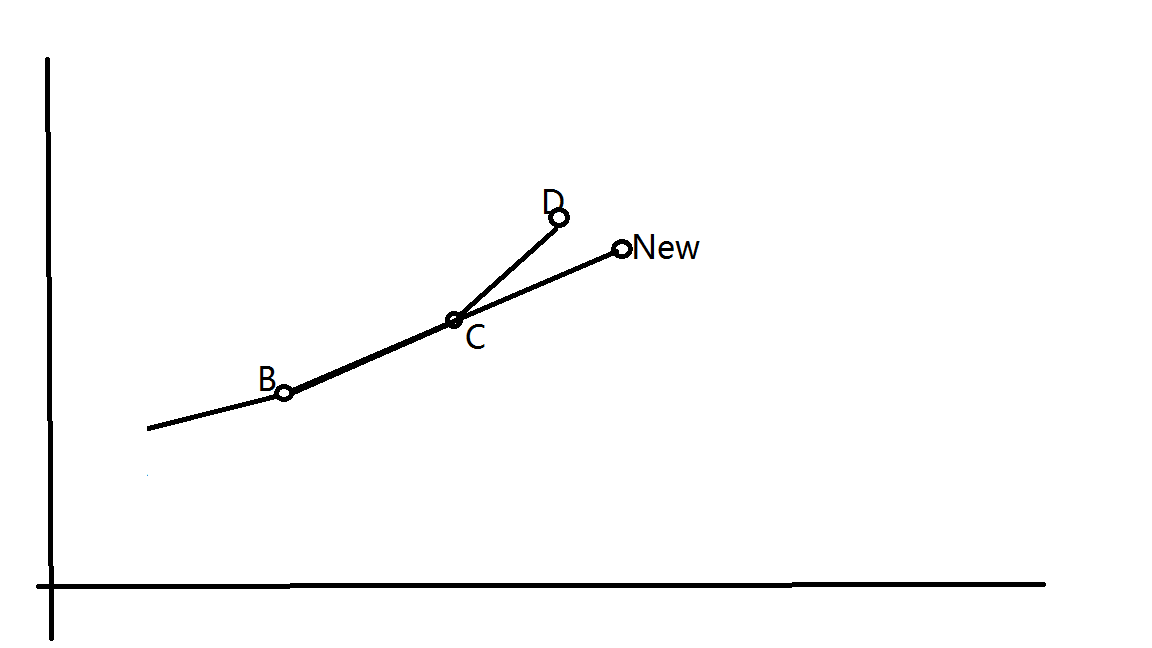
而对于这个New点，它对于之后的点，比D点更优，因为在之后转移时，CNew比CD的斜率更小，所得截距也最小。(由于f的斜率是单调递增的)

这个在凸包上的操作通过单调队列实现。

code：

#include <cstdio>
using namespace std;

int read()
{
    char c;while(c=getchar(),c<''||c>'');
    int x=c-'';while(c=getchar(),c>=''&&c<='')x=x*+c-'';
    return x;
}

typedef long long LL;
LL N,L,f[],a[];
LL sum[],S[];
LL l[],h,t;

double X(int x){return S[x];}
double Y(int y){return f[y]+(S[y]+L-)*(S[y]+L-);}
double get(int x,int y){
    return (Y(y)-Y(x))/(X(y)-X(x));
}

int main()
{
    N=read(),L=read();L++;
    register int i;
        for(i=;i<=N;i++)a[i]=read();
        for(i=;i<=N;i++){
            sum[i]=sum[i-]+a[i];
            S[i]=sum[i]+i;
        }
    h=t=;
        for(i=;i<=N;i++){
            while(h<t&&get(l[h],l[h+])<*S[i])h++;
            f[i]=f[l[h]]+(S[i]-S[l[h]]-L)*(S[i]-S[l[h]]-L);
            while(h<t&&get(l[t-],l[t])>get(l[t],i))t--;
            l[++t]=i;
        }
    printf("%lld",f[N]);
    return ;
}