关于NOI2010“超级钢琴”的反思

[NOI2010] 超级钢琴

题目描述

小 Z 是一个小有名气的钢琴家，最近 C 博士送给了小 Z 一架超级钢琴，小 Z 希望能够用这架钢琴创作出世界上最美妙的音乐。

这架超级钢琴可以弹奏出 \(n\) 个音符，编号为 \(1\) 至 \(n\)。第 \(i\) 个音符的美妙度为 \(A_i\)，其中 \(A_i\) 可正可负。

一个“超级和弦”由若干个编号连续的音符组成，包含的音符个数不少于 \(L\) 且不多于 \(R\)。我们定义超级和弦的美妙度为其包含的所有音符的美妙度之和。两个超级和弦被认为是相同的，当且仅当这两个超级和弦所包含的音符集合是相同的。

小 Z 决定创作一首由 \(k\) 个超级和弦组成的乐曲，为了使得乐曲更加动听，小 Z 要求该乐曲由 \(k\) 个不同的超级和弦组成。我们定义一首乐曲的美妙度为其所包含的所有超级和弦的美妙度之和。小 Z 想知道他能够创作出来的乐曲美妙度最大值是多少。

输入格式

输入第一行包含四个正整数 \(n, k, L, R\)。其中 \(n\) 为音符的个数，\(k\) 为乐曲所包含的超级和弦个数，\(L\) 和 \(R\) 分别是超级和弦所包含音符个数的下限和上限。

接下来 \(n\) 行，每行包含一个整数 \(A_i\)，表示按编号从小到大每个音符的美妙度。

输出格式

输出只有一个整数，表示乐曲美妙度的最大值。

样例 #1

样例输入 #1

4 3 2 3
3
2
-6
8

样例输出 #1

11

提示

样例解释

共有 \(5\) 种不同的超级和弦：

1. 音符 \(1 \sim 2\)，美妙度为 \(3+2=5\)；
2. 音符 \(2 \sim 3\)，美妙度为 \(2+(-6)=-4\)；
3. 音符 \(3 \sim 4\)，美妙度为 \((-6)+8=2\)；
4. 音符 \(1 \sim 3\)，美妙度为 \(3+2+(-6)=-1\)；
5. 音符 \(2 \sim 4\)，美妙度为 \(2+(-6)+8=4\)。

最优方案为：乐曲由和弦 \(1,3,5\) 组成，美妙度为 \(5+2+4=11\)。

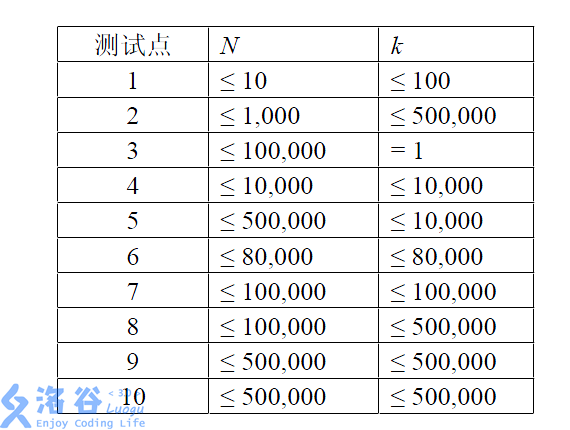
所有数据满足：\(-1000 \leq A_i \leq 1000\)，\(1 \leq L \leq R \leq n\) 且保证一定存在满足要求的乐曲。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int s[500010];
struct liu
{
	int l,r,las,id;
	friend bool operator <(liu a,liu b)
	{
		return s[a.las]-s[a.id-1]<s[b.las]-s[b.id-1];
	}
}a;
priority_queue <liu>q;
int n;
int f[1000010][25];
void init()
{
	for(int i=1;i<=n;i++)
	{
		f[i][0]=i;
	}
	for(int i=1;(1<<i)<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(s[f[j][i-1]]>s[f[j+(1<<(i-1))][i-1]])
				f[j][i]=f[j][i-1];
			else
				f[j][i]=f[j+(1<<(i-1))][i-1];
		}
	}
}
int st(int l,int r)
{
	int k=log2(r-l+1);
	if(s[f[l][k]]>s[f[r-(1<<k)+1][k]])
		return f[l][k];
	else
		return f[r-(1<<k)+1][k];
}
int main()
{
	int k,l,r;
	scanf("%d%d%d%d",&n,&k,&l,&r);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&s[i]);
		s[i]+=s[i-1];
	}
	init();
	for(int i=1;i<=n;i++)
	{
		a.id=i;
		int ll=i+l-1,rr=min(n,i+r-1);
		if(rr>=ll)
		{
			int fd=st(ll,rr);
			a.las=fd;
			a.l=ll;
			a.r=rr;
			q.push(a);
		}
	}
	long long ans=0;
	for(int i=1;i<=k;i++)
	{
		a=q.top();
		q.pop();
		ans+=(long long)(s[a.las]-s[a.id-1]);
		int ll=a.l,rr=a.r,aa=a.las;
		if(aa+1<=rr)
		{
			int fd=st(aa+1,rr);
			a.las=fd;
			a.l=aa+1;
			a.r=rr;
			q.push(a);
		}
		if(aa-1>=ll)
		{
			int fd=st(ll,aa-1);
			a.las=fd;
			a.l=ll;
			a.r=aa-1;
			q.push(a);
		}
	}
	printf("%lld",ans);
	return 0;
}

1.应用前缀和，可以把最值和和的最值结合起来

2.优先队列其实没有那么慢

3.要敢写深想

4.st表还可以和前缀和结合起来

5.一点点的失误可能会MLE