HanLP — 路径规划算法 - 求解最短路径 - 维特比(Viterbi)算法

维特比算法:从众多路径中，挑出最优的那条，他和隐马尔可夫没有强关联

---

中文分词任务

语料库 => 训练集

初始、转移、发射矩阵 => 训练过程

维特比算法，得到真正结果

训练的时候，是用不到维特比算法的，只有分词时才会使用

算法思想

维特比（Viterbi）算法属于一种动态规划算法，目标在于寻找最优路径。

用动态规划来解决隐马尔可夫的预测问题，即用动态规划求概率最大路径（最优路径）。这时一条路径对应着一个状态序列

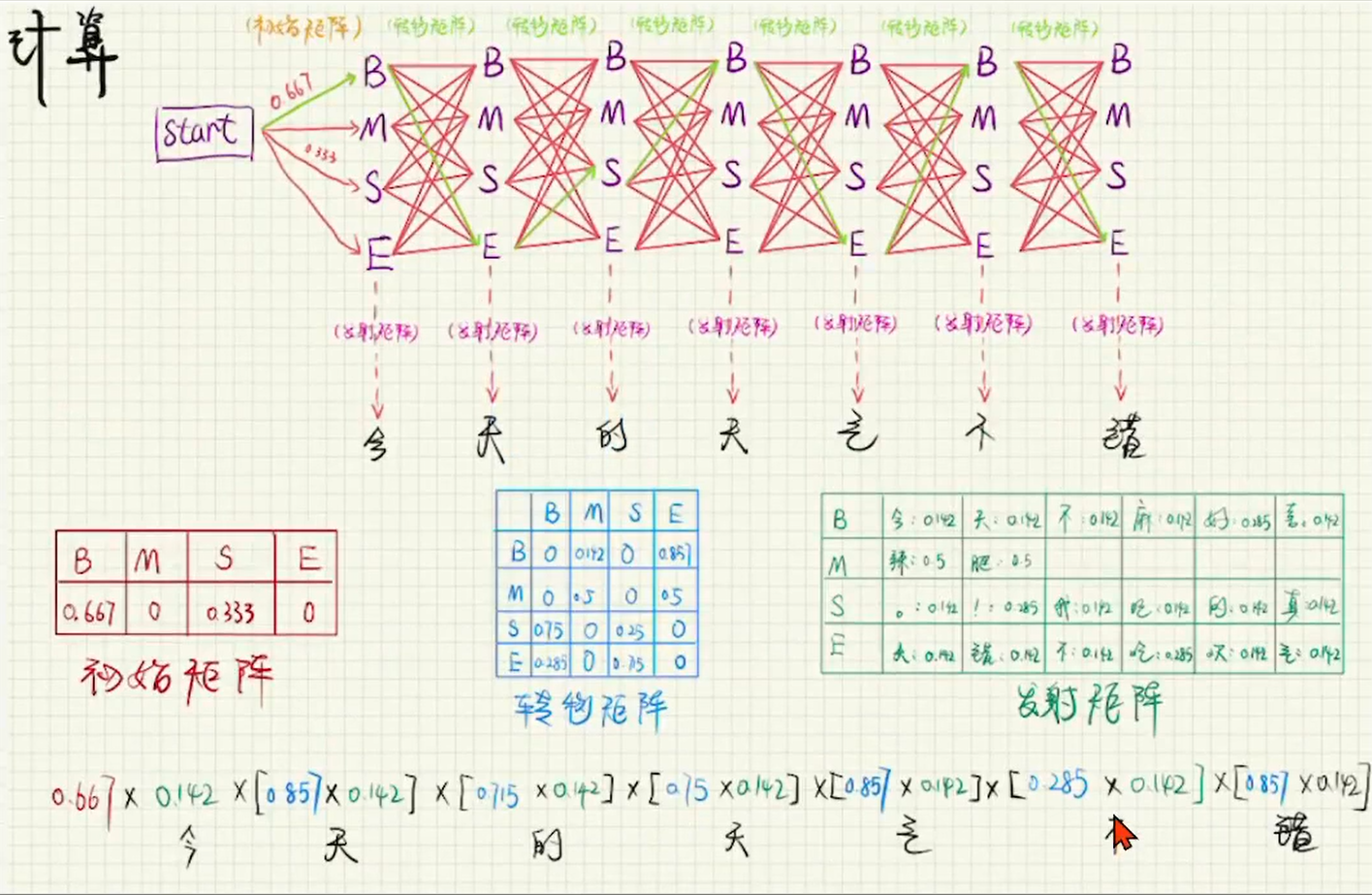
选中一条最优的路径，把节点标注出来，根据标注的节点状态序列就可以得到分词的结果了

维特比算法

从众多路径中，迅速选出最优路径

核心思想：边计算边删除，舍弃那些概率比较小的路径。

初始矩阵，人眼知道，有2个是0，ME不可能出现，但计算机不知道，也不确定某条路径就是最做优的，武断的选择B，有可能后面的概率就是0了

所以初始矩阵的4条路径，都是候选路径，

如果从B出发的话，有4条路径经过B，并且有一条最优，假设3是最优的，保存最优路径3，其它的全部删除

同理，到达M点。也是有4条路径，假设2是最优的，就把其它几条删除

从天到的

到 B 有四条，到 M 也有4条

每到达一个字都只会有4条路径，在4条路径中，选择最优的，则可得到状态序列分词结束

每个状态下连线很多，结果只有4条

代码

Viterbi.java

package com.vipsoft.viterbi;

/**
 * 维特比算法
 * @author hankcs
 */
public class Viterbi
{
    /**
     * 求解HMM模型
     * @param obs 观测序列
     * @param states 隐状态
     * @param start_p 初始概率（隐状态）
     * @param trans_p 转移概率（隐状态）
     * @param emit_p 发射概率 （隐状态表现为显状态的概率）
     * @return 最可能的序列
     */
    public static int[] compute(int[] obs, int[] states, double[] start_p, double[][] trans_p, double[][] emit_p)
    {
        double[][] V = new double[obs.length][states.length];
        int[][] path = new int[states.length][obs.length];

        for (int y : states)
        {
            V[0][y] = start_p[y] * emit_p[y][obs[0]];
            path[y][0] = y;
        }

        for (int t = 1; t < obs.length; ++t)
        {
            int[][] newpath = new int[states.length][obs.length];

            for (int y : states)
            {
                double prob = -1;
                int state;
                for (int y0 : states)
                {
                    double nprob = V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]];
                    if (nprob > prob)
                    {
                        prob = nprob;
                        state = y0;
                        // 记录最大概率
                        V[t][y] = prob;
                        // 记录路径
                        System.arraycopy(path[state], 0, newpath[y], 0, t);
                        newpath[y][t] = y;
                    }
                }
            }

            path = newpath;
        }

        double prob = -1;
        int state = 0;
        for (int y : states)
        {
            if (V[obs.length - 1][y] > prob)
            {
                prob = V[obs.length - 1][y];
                state = y;
            }
        }

        return path[state];
    }
}

WeatherExample.java

package com.vipsoft.viterbi;

import static com.vipsoft.viterbi.DoctorExample.Feel.cold;
import static com.vipsoft.viterbi.DoctorExample.Feel.dizzy;
import static com.vipsoft.viterbi.DoctorExample.Feel.normal;
import static com.vipsoft.viterbi.DoctorExample.Status.Fever;
import static com.vipsoft.viterbi.DoctorExample.Status.Healthy;

public class DoctorExample
{
    enum Status
    {
        Healthy,
        Fever,
    }
    enum Feel
    {
        normal,
        cold,
        dizzy,
    }
    static int[] states = new int[]{Healthy.ordinal(), Fever.ordinal()};
    static int[] observations = new int[]{normal.ordinal(), cold.ordinal(), dizzy.ordinal()};
    static double[] start_probability = new double[]{0.6, 0.4};
    static double[][] transititon_probability = new double[][]{
            {0.7, 0.3},
            {0.4, 0.6},
    };
    static double[][] emission_probability = new double[][]{
            {0.5, 0.4, 0.1},
            {0.1, 0.3, 0.6},
    };

    public static void main(String[] args)
    {
        int[] result = Viterbi.compute(observations, states, start_probability, transititon_probability, emission_probability);
        for (int r : result)
        {
            System.out.print(Status.values()[r] + " ");
        }
        System.out.println();
    }
}

https://github.com/hankcs/Viterbi

https://www.zhihu.com/question/20136144