自上而下的LL(1)语法分析法

LL(1)文法：从文法的开始符，向下推导，推出句子。

对文法G的句子进行确定的自顶向下语法分析的充分必要条件是，G的任意两个具有相同左部的

产生式A—>α|β 满足下列条件：

（1）如果α、β均不能推导出ε，则 FIRST(α) ∩ FIRST(β) = ∅。

（2）α 和 β 至多有一个能推导出 ε。

（3）如果 β *═> ε，则 FIRST(α) ∩ FOLLOW(A) = ∅。

将满足上述条件的文法称为LL(1)文法。

 

一、消除左递归

由于自上而下的分析方法不允许文法含有左递归。

因此对于包含直接左递归和间接左递归的文法都要消除左递归。

直接消除左递归比较容易。

例如：

　　P->Pa | b

直接消除左递归

　　P->bP'

　　P'->aP' | ε

 

二、提左因子

如果不提左因子，当面临两个相同的前缀，不知道选择哪条，必然会产生回溯。为了消除回溯，我们需要提左因子。

例如

 

 

三、实验

已知算术表达式文法 G[E]：

E → T E'

E' → + T E'｜ε

T → F T'

T' → * F T'｜ε

F → ( E )｜i

判断该文法是否为 LL(1)文法，计算 FIRST 集合和 FOLLOW 集合

SELECT(E→T E')= FIRST(T)= {(, i}

SELECT(E'→+ T E')= {+}

SELECT(E'→ε)= FOLLOW(E')= {), #}

SELECT(T→F T')= FIRST(F)= {(, i}

SELECT(T' →* F T')= {*}

SELECT(T'→ε)= FOLLOW(T')= {+, ), #}

SELECT(F → ( E ))= {(}

SELECT(F → i)= {i}

具有相同左部产生式的 SELECT 集合交集为空

SELECT(E'→+ T E')∩SELECT(E'→ε)= {+}∩{), #}=Φ

SELECT(T' →* F T')∩SELECT(T'→ε) = {*}∩{+, ), #}=Φ

SELECT(F → ( E ))∩SELECT(F → i) = {(}∩{i}=Φ

所以，转换后的文法是 LL(1)文法。

此外，我们构造LL(1)分析表

表1-1 LL(1)分析表

	i	+	*	（	）	#
E	E->TE’			E->TE’
E’		E’->+TE’			E’->ε	E’->ε
T	T->FT’			T->FT’
T’		T’->ε	T’->*FT’		T’->ε	T’->ε
F	F->i			F->(E)

 

程序如下：

 1 #include<bits/stdc++.h>
 2 #define ROW 6
 3 #define COLUMN 9
 4 using namespace std;
 5 string table[ROW][COLUMN]={
 6 {"","(",")","*","+","-","/","i","#"},
 7 {"E","Te","","","","","","Te",""},
 8 {"e","","ε","","+Te","-Te","","","ε"},
 9 {"T","Ft","","","","","","Ft",""},
10 {"t","","ε","*Ft","ε","ε","/Ft","","ε"},
11 {"F","(E)","","","","","","i",""}};
12 string Get_table(string x,string a){
13     string ans="";
14     for(int i=0;i<ROW;i++){
15         for(int j=0;j<COLUMN;j++){
16             if(x==table[i][0]&&a==table[0][j]){
17                 ans=table[i][j];
18                 return ans;
19             }
20         }
21     }
22     return ans;
23 }
24 bool check_LL1(string input){
25     bool flag=true;
26     stack < string > s;
27     s.push("#");
28     s.push("E");
29     int i=0;
30     string a=input.substr(i,1);
31     string x;
32     while(flag){
33         string RS;
34         x=s.top();
35         if(x==a && a=="#"){
36             break;
37         }else if(x==a && a!="#"){
38             s.pop();
39             i++;
40             a=input.substr(i,1);
41         }else if((RS=Get_table(x,a))!=""){
42             if(RS!="ε"){
43                 s.pop();
44                 for(int j=RS.length()-1;j>=0;j--){
45                     string tmp=RS.substr(j,1);
46                     s.push(tmp);
47                 }
48             }else{
49                 s.pop();
50             }
51         }else{
52             flag=false;
53             break;
54         }
55     }
56     return flag;
57 }
58 int main(){
59     string input;
60     while(cin>>input){
61         input=input+"#";
62         if(check_LL1(input)){
63             cout<<"correct"<<endl;
64         }else{
65             cout<<"error"<<endl;
66         }
67     }
68     return 0;
69 }

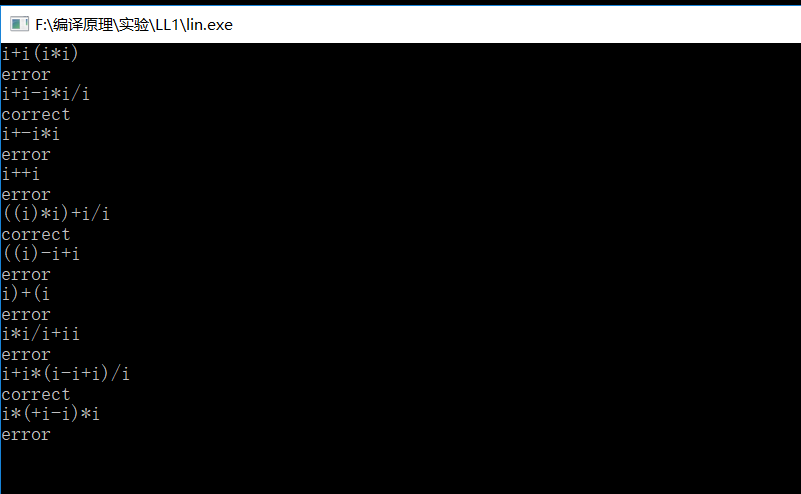
实验截图：