Bézier surface(贝塞尔曲面)

Bézier surface（贝赛尔曲面）

贝塞尔曲面是一种用于计算机图形学、计算机辅助设计和有限元建模的数学样条。与贝塞尔曲线一样，贝塞尔曲面由一组控制点定义。与插值在许多方面相似，一个关键的区别是表面通常不通过中央控制点；相反，它向他们“伸展”,好像每个人都是一种吸引力。它们在视觉上是直观的，对于许多应用来说，在数学上是方便的。

给定的贝氏度(n，m)曲面由一组(n + 1)(m + 1)控制点ki，j定义，它将单位正方形映射为嵌入在与{ ki，j }相同维数的空间中的光滑连续曲面。例如，如果k是四维空间中的所有点，那么曲面将在四维空间中。 二维贝塞尔曲面可以定义为参数曲面，其中点p的位置作为参数坐标u，v的函数由下式给出:

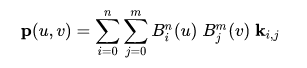
在单位平方上评估，其中

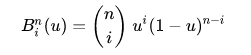
是伯恩斯坦多项式，并且

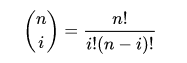
是二项式系数。

贝塞尔曲面的一些性质:

贝塞尔曲面在所有线性变换和平移下将以与其控制点相同的方式变换。

(u，v)空间中的所有u =常数和v =常数线，尤其是变形的(u，v)单位正方形的所有四条边都是贝塞尔曲线。

贝塞尔曲面将完全位于其控制点的凸包内，因此也完全位于任何给定笛卡尔坐标系中其控制点的边界框内。

面片中与变形单位正方形的角对应的点与四个控制点重合。

然而，贝塞尔曲面通常不会穿过其其他控制点。

通常，贝塞尔曲面最常见的用途是作为双三次曲面网(其中m = n = 3)。因此，单个双三次曲面片的几何形状完全由一组16个控制点定义。这些曲线通常以类似于贝塞尔曲线链接形成B样条曲线的方式链接形成B样条曲面。 更简单的贝塞尔曲面由双二次曲面片(m = n = 2)或贝塞尔三角形构成。