Tarjan求桥

传送门（poj3177）

这道题是Tarjan求桥的模板题。大意是要求在原图上加上数量最少的边，使得整张图成为一个边双联通分量。

具体的做法是，先在图中求出所有的桥，之后把边双联通分量缩成点，这样的话原图就变成了一棵树。之后，我们就在叶子之间加边即可。如何加最少的边呢？好像第一眼看上去，随便在两个叶子中间加一条边就能减少两个叶子，但事实上不是这样的，如果这两个叶子中间的路径数小于等于1条的话，将新形成的边双联通分量缩点之后有可能出现新的叶子。就像这张图一样，如果连接红色的边，那么新的图会多出一个叶子。

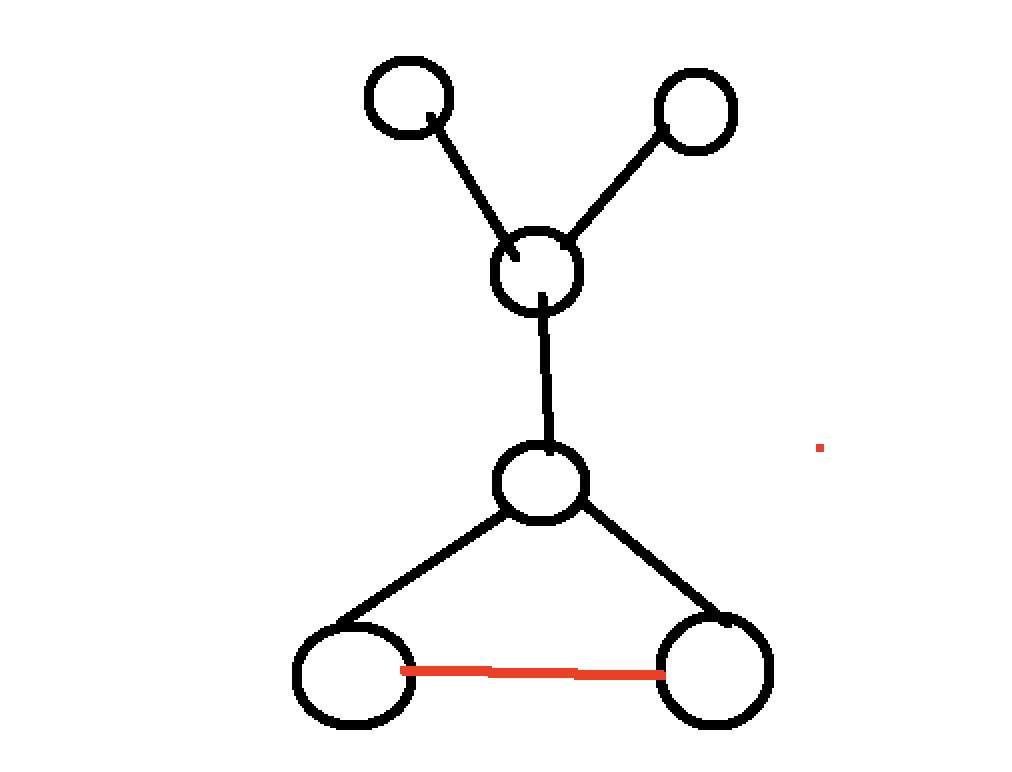
这个是因为路径上的边数只有一条，如果我们选择两点路径上边数大于1的两个叶子合并，那么一定会形成一个新的边双联通分量，而且不会有新的叶子。

因为这样的话那个新的边双肯定是至少有两个度的，那他就不会成为叶子，而如果只有一条的话，它的度就是1，那么就形成新的叶子了。

我们要这样去合并：

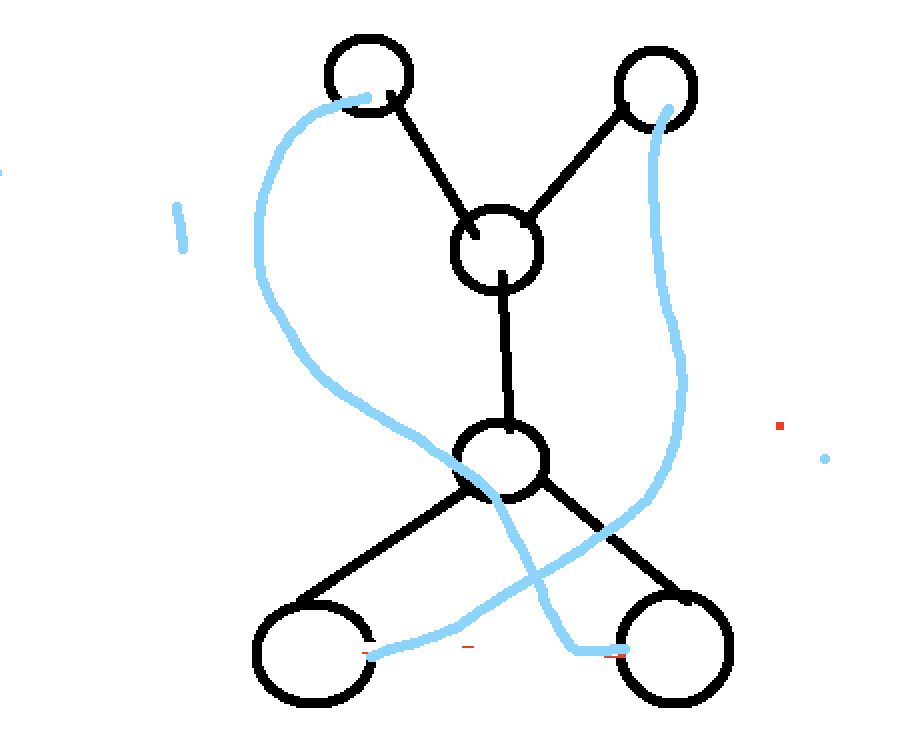
这样就可以啦！所以我们最后能得出的结论就是，需要加的边数=（叶子个数+1) >> 1.

那我们直接求桥，之后缩点，求出每个点最后的度然后计算一下就行。

然后这题因为有重边就很难受……一开始我是直接判断如果是父亲就不管，但是这样不行……因为有重边的就不是桥了，他是需要父亲去更新的，所以后来判断一下，只有树边的那条反向边我们给他特判掉，其他的都能正常更新。

看一下代码。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
#include<cstring>
#define rep(i,a,n) for(int i = a;i <= n;i++)
#define per(i,n,a) for(int i = n;i >= a;i--)
#define enter putchar('\n')
#define pr pair<int,int>
#define mp make_pair
#define fi first
#define sc second
using namespace std;
typedef long long ll;
const int M = ;
const int N = ;

int read()
{
    int ans = ,op = ;
    char ch = getchar();
    while(ch < '' || ch > '')
    {
    if(ch == '-') op = -;
    ch = getchar();
    }
    while(ch >='' && ch <= '')
    {
    ans *= ;
    ans += ch - '';
    ch = getchar();
    }
    return ans * op;
}

struct edge
{
    int next,to,from;
}e[M];

int f,r,x,y,ecnt = -,head[M],dfn[M],low[M],scc[M],stack[M],top,cnt,rdeg[M],ans,idx;
bool vis[M],pd[M];

void add(int x,int y)
{
    e[++ecnt].to = y;
    e[ecnt].from = x;
    e[ecnt].next = head[x];
    head[x] = ecnt;
}

void tarjan(int x,int g)
{
    bool flag = ;
    vis[x] = ,stack[++top] = x;
    dfn[x] = low[x] = ++idx;
    for(int i = head[x];~i;i = e[i].next)
    {
    //if(pd[i]) continue;
    //pd[i] = pd[i^1] = 1;
    if(e[i].to == g && !flag)
    {
        flag = ;
        continue;
    }
    if(!dfn[e[i].to]) tarjan(e[i].to,x),low[x] = min(low[x],low[e[i].to]);
    else if(vis[e[i].to])low[x] = min(low[x],dfn[e[i].to]);
    }
    if(low[x] == dfn[x])
    {
    int p;
    cnt++;
    while((p = stack[top--]))
    {
        scc[p] = cnt,vis[p] = ;
        if(p == x) break;
    }
    }
}

int main()
{
    memset(head,-,sizeof(head));
    f = read(),r = read();
    rep(i,,r) x = read(),y = read(),add(x,y),add(y,x);
    rep(i,,f) if(!dfn[i]) tarjan(i,i);
    rep(i,,f)
    {
    for(int j = head[i];~j;j = e[j].next)
    {
        int r1 = scc[e[j].to],r2 = scc[i];
        if(r1 != r2) rdeg[r1]++,rdeg[r2]++;
    }
    }
    rep(i,,cnt) if(rdeg[i] == ) ans++;
    printf("%d\n",(ans+) >> );
    return ;
}