LeetCode 307. 区域和检索 - 数组可修改

地址 https://leetcode-cn.com/problems/range-sum-query-mutable/

题目描述
给定一个整数数组  nums，求出数组从索引 i 到 j  (i ≤ j) 范围内元素的总和，包含 i,  j 两点。

update(i, val) 函数可以通过将下标为 i 的数值更新为 val，从而对数列进行修改。

示例:

Given nums = [, , ]

sumRange(, ) ->
update(, )
sumRange(, ) ->
说明:

数组仅可以在 update 函数下进行修改。
你可以假设 update 函数与 sumRange 函数的调用次数是均匀分布的。

算法1
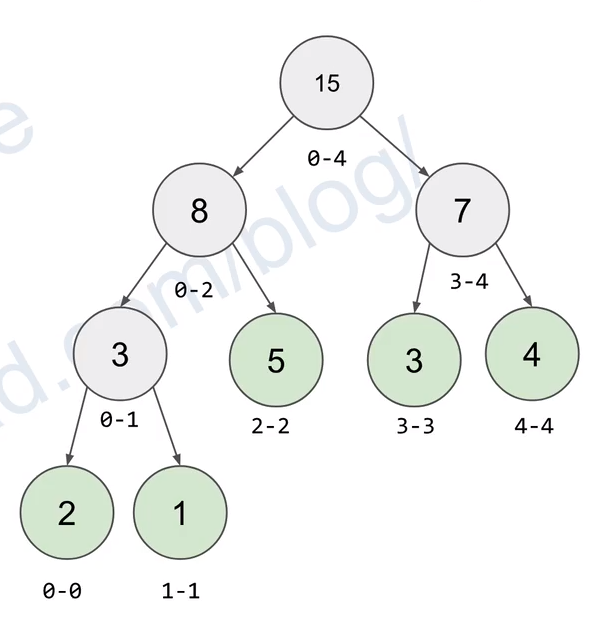
区间求和 自然使用 线段树 或者线段数组
这里以线段树为例
以 空间换时间 记录线段之间的和 最大最小值等
由于是树 即使其中一部分元素改变或者某一个元素改变 更改记录也只是log（n）的复杂度

class SegmentTreeNode {
public:
    SegmentTreeNode(int start,int end,int sum,
        SegmentTreeNode* left = nullptr,
        SegmentTreeNode* right = nullptr):
        start(start),
        end(end),
        sum(sum),
        left(left),
        right(right){}
    SegmentTreeNode(const SegmentTreeNode&) = delete;
    SegmentTreeNode& operator=(const SegmentTreeNode&) = delete;
    ~SegmentTreeNode() {
        delete left;
        delete right;
        left = right = nullptr;
    }

    int start;
    int  end;
    int sum;
    SegmentTreeNode* left;
    SegmentTreeNode* right;
};

class NumArray {
public:
    NumArray(vector<int> nums) {
        nums_.swap(nums);
        if (!nums_.empty())
            root_.reset(buildTree(, nums_.size() - ));
    }

    void update(int i, int val) {
        updateTree(root_.get(), i, val);
    }

    int sumRange(int i, int j) {
        return sumRange(root_.get(), i, j);
    }
private:
    vector<int> nums_;
    std::unique_ptr<SegmentTreeNode> root_;

    SegmentTreeNode* buildTree(int start, int end) {
        if (start == end) {
            return new SegmentTreeNode(start, end, nums_[start]);
        }
        int mid = start + (end - start) / ;
        auto left = buildTree(start, mid);
        auto right = buildTree(mid + , end);
        auto node = new SegmentTreeNode(start, end, left->sum + right->sum,
            left, right);

        return node;
    }

    void updateTree(SegmentTreeNode* root, int i, int val) {
        if (root->start == i && root->end == i) {
            root->sum = val;
            return;
        }
        int mid = root->start + (root->end - root->start) / ;
        if (i <= mid) {
            updateTree(root->left, i, val);
        }
        else {
            updateTree(root->right, i, val);
        }
        root->sum = root->left->sum + root->right->sum;
    }

    int sumRange(SegmentTreeNode* root, int i, int j) {
        if (i == root->start && j == root->end) {
            return root->sum;
        }
        int mid = root->start + (root->end - root->start) / ;
        if (j <= mid) {
            return sumRange(root->left, i, j);
        }
        else if (i > mid) {
            return sumRange(root->right, i, j);
        }
        else {
            return sumRange(root->left, i, mid) + sumRange(root->right, mid + , j);
        }
    }
};