最短路算法 Dijkstra 入门

dijkstra算法 是一种单源点最短路算法求出一个点到其他所有点的最短路。

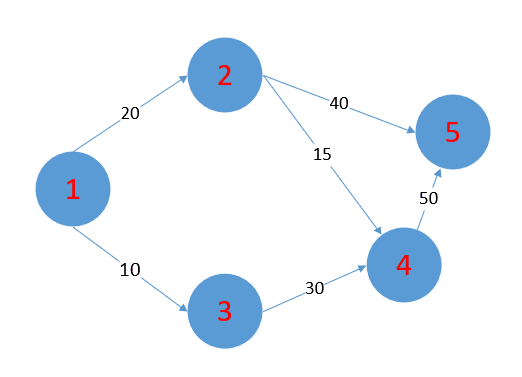
给你这样的一个图，需要求出1号点到其他点的最短距离是多少。

首先我们开一个数组 d[N]，d[x] 代表着从起点出发到x点的距离是多少。

开一个数组vis[N], vis[x]数组代表着某个点d[x]是不是成为定值，不会再变小了。

然后我们在开一个数组，edge[N][N]，edge[a][b] 代表着从a点走到b的路程是多少。

如果不存在 a->b的这条边，那么就将他设置为-1。

更新d数组的条件：d[a] > d[b] + edge[b][a] 的时候更新d[a]的值。

一开始我们将所有距离设置都设置 inf ( inf 意为无穷大）。

当然d[s] = 0;

所以对于刚开始的数组d[]来说他的值应该为

图的状态应该是

现在我们从1号点出发，图上存在一个 1->3的边 距离为 10  存在一个1->2的边 距离为20。

那么d[3] =  min(d[3], d[1] + edge[1][3]) d[2] = min(d[2], d[1] + edge[1][2])

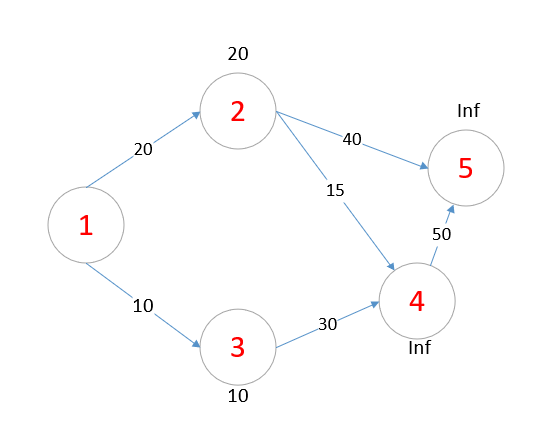
d数组即被更新成

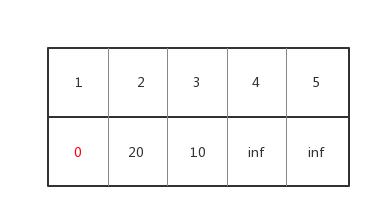
其中vis[1] = 1，即这个点不会的距离不会在变小了。

我们扫一遍d数组，跳过vis[x] == 1的点，找到d[x]最小的点，通过上面的那个数组我们可以发现，这个点是3，

我们把 vis[3] = 1， 然后再通过3号点出发更新d[].

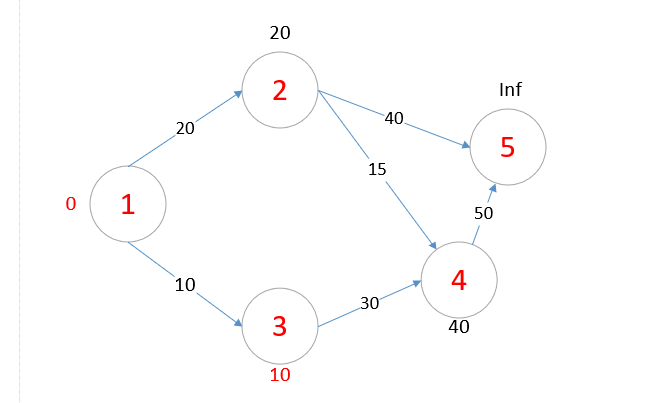
　　 d数组的值为

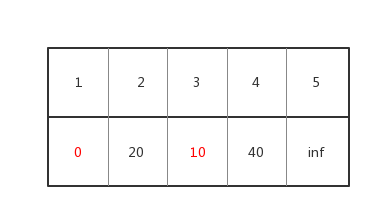
然后我们继续找到d[x]最小的且没被标记过的点  由上表可知是点2

我们标记点2，然后再用2号点出发，看看有没有点的距离可以被更新成更小的。

当我们走完2号点的边的时候，图就会变成

d数组的结果为

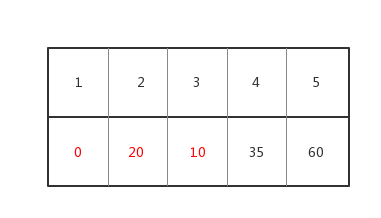
我们继续找到d[x]最小的且没被标记过的点  由上表可知是点4

我们先标记4号点，然后通过点4出发，然后看一下出4号点出发，有没有点的d会被更新成更小的值

d数组的结果为

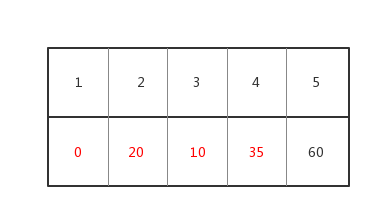
最后没标记过的点只有5了， 我们从5号点出发，看看有没有点会继续被更新。

我们得到最后的图就变成了

d数组最后就被更新成了

这样我们就进行完了dijkstra算法。

从原点出发到各个点的最短路径是多少就求出来了。

假设 d[a] < d[b] ， 并且存在edge[a][b] ， 那么因为边edge[a][b] > 0，那么不可能通过 b 点去更新 a 点， 只可能从a点出发然后到b点，使得d[b]的更小。

因为更新的条件是  d[b] > d[a] + edge[a][b]。 所以只有从d[]更小的点出发才有可能使得别的点更小。

总结下来的话，就是从原点出发，每次都选出当前距离里原点最近的点(跳过标记过的点）x，然后从x点出发，遍历x点的所有边，看一下是不是存在别的点可以通过点x往外走，使得原点到目标点的距离更小，并且标记一下点x，下次不会再选择x，因为x已经是最小的了。

每次都确立一个点，确立完一个点后需要其访问所有点去更新距离，总有由n个点

所以 时间复杂度是 n * 2n

来一个题目：

HDU 2544

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<algorithm>
 using namespace std;
 int edge[+][+];
 int d[+];
 bool vis[+];
 const int inf = 0x3f3f3f3f;
 int main()
 {
     int n, m;
     while(~scanf("%d%d",&n,&m)&& (n || m)){
         int a,b,c;
         memset(edge, -, sizeof(edge));
         memset(d, inf, sizeof(d));
         memset(vis, , sizeof(vis));
         while (m--){
             scanf("%d%d%d", &a, &b, &c);
             edge[a][b] = edge[b][a] = c;
         }
         for(int i = ;i <= n;i++ ){
             if(edge[][i] == -) continue;
             d[i] = edge[][i];
         }
         d[] = ;
         vis[] = ;
         while (){
             int min1 = inf,z = -;
             for (int j = ;j <= n; j++)
                 if(!vis[j] && min1 > d[j])
                     z = j, min1 = d[j];
             if(z == -) break;
             vis[z] = ;
             for (int j = ; j <= n ; j++){
                 if(edge[z][j] == -) continue;
                 d[j] = min(d[j], d[z] + edge[z][j]);
             }
         }
         printf("%d\n", d[n]);
     }
     return ;
 }

现在这个是时空复杂度最高的代码。

接来下还有关于dijkstra优化的传送门。