Relatively Prime Graph CF1009D 暴力 思维

Relatively Prime Graph

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's call an undirected graph G=(V,E)G=(V,E) relatively prime if and only if for each edge (v,u)∈E(v,u)∈E  GCD(v,u)=1GCD(v,u)=1 (the greatest common divisor of vv and uu is 11). If there is no edge between some pair of vertices vv and uu then the value of GCD(v,u)GCD(v,u) doesn't matter. The vertices are numbered from 11 to |V||V|.

Construct a relatively prime graph with nn vertices and mm edges such that it is connected and it contains neither self-loops nor multiple edges.

If there exists no valid graph with the given number of vertices and edges then output "Impossible".

If there are multiple answers then print any of them.

Input

The only line contains two integers nn and mm (1≤n,m≤1051≤n,m≤105) — the number of vertices and the number of edges.

Output

If there exists no valid graph with the given number of vertices and edges then output "Impossible".

Otherwise print the answer in the following format:

The first line should contain the word "Possible".

The ii-th of the next mm lines should contain the ii-th edge (vi,ui)(vi,ui) of the resulting graph (1≤vi,ui≤n,vi≠ui1≤vi,ui≤n,vi≠ui). For each pair (v,u)(v,u) there can be no more pairs (v,u)(v,u) or (u,v)(u,v). The vertices are numbered from 11 to nn.

If there are multiple answers then print any of them.

Examples

input

Copy

5 6

output

Copy

Possible
2 5
3 2
5 1
3 4
4 1
5 4

input

Copy

6 12

output

Copy

Impossible

Note

Here is the representation of the graph from the first example: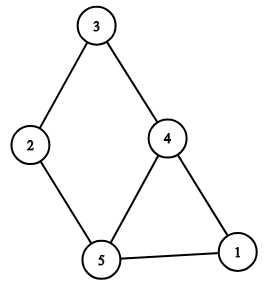

emmm，没想到直接暴力过了。。

直接暴力最大公约数为1的对数，当对数超过m直接break，没有时间超限

#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <string>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#define debug(a) cout << #a << " " << a << endl
using namespace std;
const int maxn = 1e5 + 10;
const int mod = 1e9 + 7;
typedef long long ll;
vector< pair<ll,ll> > edge;
ll gcd( ll a, ll b ) {
    if( a == 0 ) {
        return b;
    } else if( b == 0 ) {
        return a;
    }
    return gcd( b, a%b );
}
int main() {
    ll n, m;
    cin >> n >> m;
    if( m < n-1 ) {
        cout << "Impossible" << endl;
    } else {
        for( ll i = 1; i < n; i ++ ) {
            for( ll j = i+1; j <= n; j ++ ) {
                if( gcd(i,j) == 1) {
                    edge.push_back(make_pair(i,j));
                    if( edge.size() > m ) {
                        break;
                    }
                }
            }
        }
        if( edge.size() < m ) {
            cout << "Impossible" << endl;
        } else {
            cout << "Possible" << endl;
            for( ll i = 0; i < m; i ++ ) {
                cout << edge[i].first << " " << edge[i].second << endl;
            }
        }
    }
    return 0;
}