2019.6.5 NOIP2014 day2 t2 寻找道路

我竟然一个人敲了NOIP提高组的t2？

---

题目描述

在有向图 G 中，每条边的长度均为 1，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1. 路径上的所有点的出边所指向的点都直接或间接与终点连通。
2. 在满足条件1的情况下使路径最短。

注意：图 G 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入输出格式

输入格式：

第一行有两个用一个空格隔开的整数 n 和 m，表示图有 n 个点和 m 条边。

接下来的 m 行每行 2 个整数 x,y，之间用一个空格隔开，表示有一条边从点 x 指向点 y。

最后一行有两个用一个空格隔开的整数 s,t，表示起点为 s，终点为 t。

输出格式：

输出只有一行，包含一个整数，表示满足题目描述的最短路径的长度。如果这样的路径不存在，输出-1。

输入输出样例

输入样例#1：

3 2
1 2
2 1
1 3

输出样例#1：

-1

输入样例#2：

6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5

输出样例#2：

3

说明

解释1：

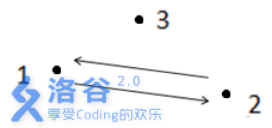
如上图所示，箭头表示有向道路，圆点表示城市。起点11与终点33不连通，所以满足题目描述的路径不存在，故输出−1 。

解释2：

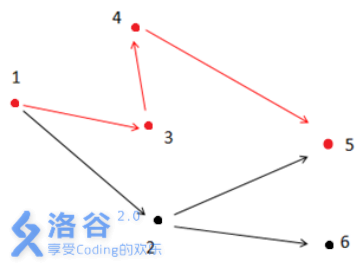
如上图所示，满足条件的路径为1- >3- >4- >5。注意点2 不能在答案路径中，因为点2连了一条边到点6 ，而点6不与终点5 连通。

【数据范围】

对于30%的数据，0<n≤10，0<m≤20;

对于60%的数据，0<n≤100，0<m≤2000;

对于100%的数据，0 < n ≤10000, 0 < m ≤ 200000,0<n≤10000,0<m≤200000,0<x,y,s,t≤n,x,s≠t。

---

由题意 只需要跑一遍最短路 重点注意处理不符合要求的点

只需要反向建图，再用BFS找到所有原图中不能到达终点的点（即反向建图后终点不能到达的点），标记为book[i]=0；

再用O(m)的复杂度扫描每一条边，如果与点i联通的点中有book[j]=0的，则标记mark[i]=0（注意不是book[i]=0，原因在于点i本身可以到达终点）。

上代码

#include<iostream>
#include<queue>
#include<cstring>
#include<utility>
#include<cstdio>
#define inf 0x3f3f3f3f
using namespace std;
int n,m,head1[],head2[],num1,num2,vst[],a,b,book[],s,t,d[],mark[];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q1;
struct edge
{
    int u,v,nxt;
}e1[],e2[];
queue<int> q;
void add1(int u,int v)
{
    e1[++num1].u=u,e1[num1].v=v;
    e1[num1].nxt=head1[u],head1[u]=num1;
}
void add2(int u,int v)
{
    e2[++num2].u=u,e2[num2].v=v;
    e2[num2].nxt=head2[u],head2[u]=num2;
}
int main()
{
    memset(head1,-,sizeof head1);
    memset(head2,-,sizeof head2);
    memset(d,inf,sizeof d);
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++)
    {
        scanf("%d%d",&a,&b);
        if(a==b)continue;
        add1(a,b);
        add2(b,a);//反向建图
    }
    scanf("%d%d",&s,&t);
    book[t]=;
    q.push(t);
    while(!q.empty())
    {
        int st=q.front();
        q.pop();
        for(int i=head2[st];i!=-;i=e2[i].nxt)
        {
            if(book[e2[i].v]==)continue;
            book[e2[i].v]=;
            q.push(e2[i].v);
        }
    }//BFS
    for(int i=;i<=n;i++)mark[i]=;
    for(int i=;i<=n;i++)
    {
        for(int j=head1[i];j!=-;j=e1[j].nxt)
        {
            if(book[e1[j].v]==)mark[e1[j].u]=;
        }
    }//记录非法的点
    q1.push(make_pair(,s));
    d[s]=;
    while(!q1.empty())
    {
        int x=q1.top().second;
        q1.pop();
        if(vst[x]==||mark[x]==)continue;
        vst[x]++;
        for(int st=head1[x];st!=-;st=e1[st].nxt)
        {
            if(d[e1[st].v]>d[e1[st].u]+)
            {
                d[e1[st].v]=d[e1[st].u]+;
                q1.push(make_pair(d[e1[st].v],e1[st].v));
            }
        }
    }//dijkstra最短路
    if(d[t]==)
    {
        puts("-1");//无解输出-1
        return ;
    }
    printf("%d",d[t]);
    return ;
}