数学--数论--HDU 6063 RXD and math （跟莫比乌斯没有半毛钱关系的打表）

RXD is a good mathematician.

One day he wants to calculate:



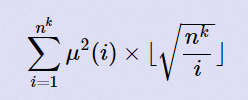
output the answer module 109+7.

p1,p2,p3…pk are different prime numbers

Input

There are several test cases, please keep reading until EOF.

There are exact 10000 cases.

For each test case, there are 2 numbers n,k.

Output

For each test case, output “Case #x: y”, which means the test case number and the answer.

Sample Input

10 10

Sample Output

Case #1: 999999937

看见这个题不可能去正常做，尝试达标找规律，然后找了 n^K的规律

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9 + 7;
ll ksm(ll n, ll k)
{
    ll r = 1;
    for (; k; k >>= 1)
    {
        if (k & 1)
            r = r * n % mod;
        n = n * n % mod;
    }
    return r;
}

int main()
{
    ll x, y, ca = 1;
    while (~scanf("%lld%lld", &x, &y))
    {
       // x大于mod这题就没法做了
        x=x%mod; //利用费马小定理
        cout << "Case #" << ca++ << ": " << ksm(x, y) << endl;
    }
}