Paper Review: Epigenetic Landscape, Cell Differentiation 01

Today, I'll share a review papers about Epigenetic Landscape, the Epigenetic Landscape is related to cell differentiation. It comes from Current Biology, published in 2012.

Bistability, Bifurcations, and Waddington’s Epigenetic Landscape [1]

This paper mainly introduces a different bifurcation theory, which is related to the cell-fate decision. This method is the saddle-node bifurcation, it's different from the supercritical pitchfork bifurcation in the Waddington's original picture.

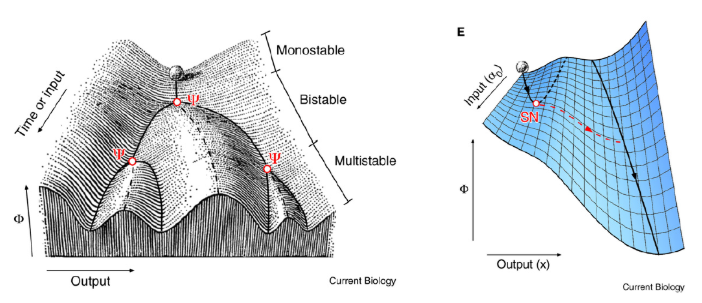
The left figure is supercritical pitchfork bifurcation and the right figure is the saddle-node bifurcation. The former is corresponding to the appearance of new valleys, but the latter is corresponding to the disappearance of valleys. Specifically, for the latter theory, if the ball goes into the right valley, the previous left valley will vanish, which provides intrinsic irreversibility to the process of differentiation, but this type of irreversibility is missing from the Waddington's original picture.

In the following, they examine models of two important developmental processes, cell-fate induction and lateral inhibition (a symmetrical cell-cell competition process). The cell-fate induction supports the saddle-node bifurcation theory, and lateral inhibition corresponds better to Waddington’s picture.

P.S.: Additional background information on the dynamical systems theory used here can be found in chapter 2 of Strogatz’s textbook [2]. Further information on cell-fate induction and cell-cell competition can be found in chapter 3 of Gilbert’s textbook [3].

Glossary:

Stable steady states VS. Unstable steady states (The following figure comes from this link):

Attractor: Stable steady states are attractors.

Positive feedback: The gene regulation part of the biology section.

Bifurcation: A splitting of one thing into two. For one-variable systems, there are three classes of bifurcations: saddle-node bifurcations, pitchfork bifurcations, and transcritical bifurcations.

Bistability: Having two stable steady states or two potential wells.

Hill function: 

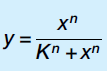
For n > 1 the Hill function yields a sigmoidal curve. The parameter K is the concentration of x at which the response is half-maximal. The exponent n determines how switch-like the response is. The Hill function usually provides a simple, reasonably accurate approximation for these sigmoidal responses. (Biological response functions are often well-approximated by Hill functions. So, the feedback component in Equation 1 consists of a Hill function.)

Potential: Compared with the real life, a vector field of forces can be calculated from a scalar field of potentials by taking derivatives. For biochemical reactions one begins with a field of velocities rather than a field of forces, and one can define the potential as a function which, when differentiated, yields this velocity field.

 Cell-Fate Induction:

In cell-fate induction, a cell or a group of cells produces an inductive stimulus that causes another cell to adopt a new phenotype.

The mathematical model (single variable): basal rate of x synthesis + a feedback-dependent component of x synthesis

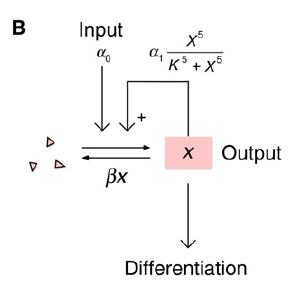
x: some differentiation regulator promotes its own synthesis via a positive feedback loop;

α0: some basal rate of x synthesis;

α1: maximum rate of feedback-dependent synthesis of x;

K: concentration of x;

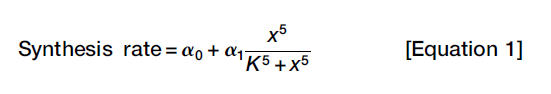
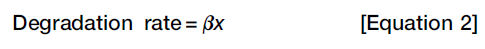
From Equation 1 and 2, we can get:

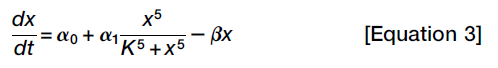
To visualize functions of x’s rates of production and degradation:

Steady states are found where the production and degradation rates are equal and the two curves intersect. Two of the intersections correspond to stable steady states, one with x = 0 and the other with x≈1.7, and the middle one corresponds to an unstable steady state.

Next the steady states are depicted in a Waddington-like potential framework. The potential Φ is defined as a function whose derivative dΦ/dx yields the speed at which x moves toward its steady state. (dx/dt can be seen as the speed, so Φ as the corresponding integral form.)

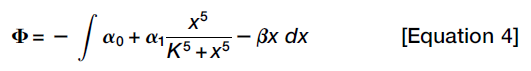
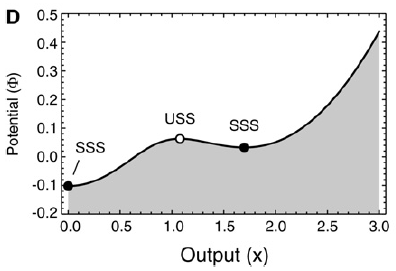
In the case of biochemical reaction networks, however, dΦ/dx determines x’s velocity rather than acceleration, so that a ball rolling down a constant slope would travel at a constant speed. When the ball reached the bottom of a potential well, it would not just stop accelerating, it would stop moving.

Furthermore, the steepness of the valley walls, or the canalization of the cell fate, in Waddington’s terminology, is determined by the nonlinearity of the positive feedback: the higher the Hill coefficient, the steeper the valley walls, making the cell fate more robust with respect to perturbations in x.

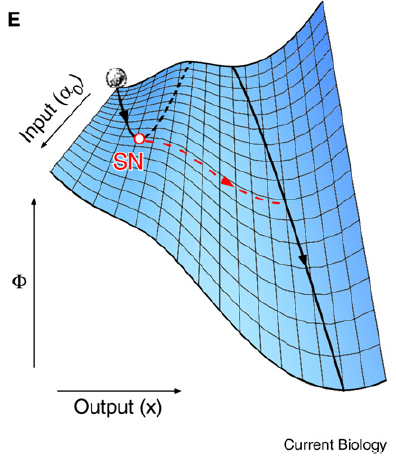
Different with Waddington's epigenetic landscape model, the model here (Saddle-Node Landscape) in cell-fate induction eliminates valleys rather than creating new valleys. The cell leaves the uninduced cell fate and adopts the induced cell fate, because the valley corresponding to the uninduced cell fate no longer exists.

Other differences between the Saddle-Node Landscape and Waddington’s Epigenetic Landscape: (1)The Instability of Intermediate States. (2)The Irreversibility of Cell-Fate Commitment (saddle is irreversibility and Waddington is reversibility). (3)The Narrowing of Developmental Potential during Differentiation (Both models. but Waddington narrowed by the ridge, and saddle narrowed by the disappearance of the valley).

Lateral Inhibition:

a process where new fates are created through cell-cell competition.

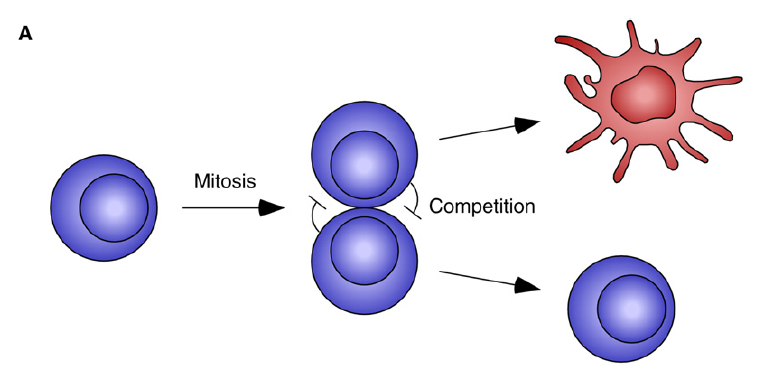
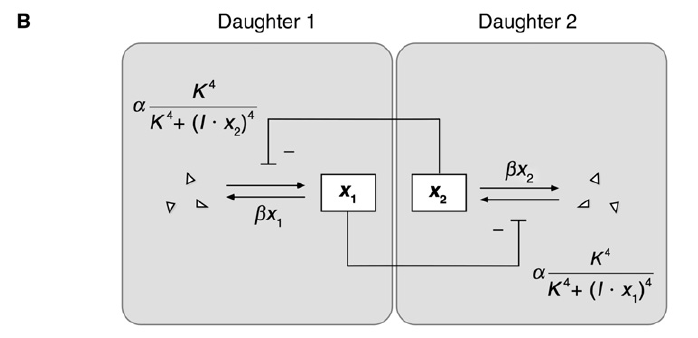
The mathematical model (a simple model of mutual inhibition)

x: In the mother cell the Delta protein;

α: basal production rate;

β: degraded rate;

After cell division, x -> x1 and x2, then assume x1 and x1 inhibits each other (Using an inhibitory Hill function to describe this interaction).

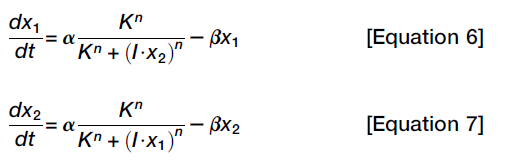
This system has gone through a pitchfork bifurcation, the key here is that the system is symmetrical (The key to the pitchfork bifurcation is the symmetry of the ruler). In addition, it's reversible, but some scholars adding some feedback loops in order to making it irreversible.

Thus, the type of bifurcation depends both upon how the system is wired and how the stimulus affects the system.

Sum up:

1. proposing that differentiation mainly involves the disappearance of valleys from the landscape, not the appearance of new valleys;

2. proposing that the disappearance of the valleys occurs through saddle-node bifurcations, which provide an intrinsic irreversibility to the process of differentiation, a type of irreversibility missing from Waddington’s original picture.

3. the processes depicted on Waddington’s original landscape correspond to intrinsically reversible pitchfork bifurcations, which could correspond to symmetry-breaking, intrinsically reversible developmental events like the generation of new cell fates through cell– cell competition.

Few experience: For a system to be bistable or multistable, it must include positive or double-negative feedback loops [1]; Biological response functions are often well-approximated by Hill functions[1];

Ref:

[1]. Ferrell Jr J E. Bistability, bifurcations, and Waddington's epigenetic landscape[J]. Current biology, 2012, 22(11): R458-R466.

[2]. Strogatz, S.H. (1994). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (Cambridge MA: Westview Press).

[3]. Gilbert, S.F. (2010). Developmental Biology, Ninth Edition (Sunderland MA: Sinauer Associates).