搜索+简单dp

前言:即使是简单的递归，在复杂度过高时也可以使用简单的dp。

一般有两种情况，一是利用dp思想求最优子结构进行搜索剪枝，二是利用搜索进行dp数组的填充。

例题一、hdu1978

题目大意：这是一个简单的生存游戏，你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下：

1.机器人一开始在棋盘的起始点并有起始点所标有的能量。

2.机器人只能向右或者向下走，并且每走一步消耗一单位能量。

3.机器人不能在原地停留。

4.当机器人选择了一条可行路径后，当他走到这条路径的终点时，他将只有终点所标记的能量。



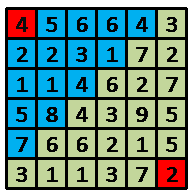
如上图，机器人一开始在(1,1)点，并拥有4单位能量，蓝色方块表示他所能到达的点，如果他在这次路径选择中选择的终点是(2,4)

点，当他到达(2,4)点时将拥有1单位的能量，并开始下一次路径选择，直到到达(6,6)点。

我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数，输出的结果对10000取模。

一开始的思路：既然已知迷宫起点终点，果断dfs。

dfs最重要的一点就是明确函数中应有的参数和结束条件

在这里，很显然终止条件是到达右下角的点，所以函数中参数要有x,y坐标。又因为在每个点有对应的能量，由能量决定下一步能走到哪里进行枚举，所以参数还应该包含当前点的能量。

#include <bits/stdc++.h>
using namespace std;
int n,m,a[109][109];
int ans;//答案
bool p(int q,int w)
{
	if(q>=0&&q<n&&w>=0&&w<m)
		return true;
	else
		return false;
}
void dfs(int power,int x,int y)
{
	if(x==n-1&&y==m-1)
	{
		ans++;
		ans%=10000;
		return;
	}
	for(int i=0;i<=power;i++)
	{
		if(x+i>=n)
			break;
		for(int j=0;j<=power-i;j++)
		{
			if(y+j>=m)
				break;
			if(i==0&&j==0)
				continue;
			dfs(a[x+i][y+j],x+i,y+j);
		}
	}
}
int main()
{
	int t;
	cin>>t;
	while(t--)
	{
		cin>>n>>m;
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<m;j++)
				cin>>a[i][j];
		}
		dfs(a[0][0],0,0);
		cout<<ans;
	}
}

很遗憾，完全超时。想来也是，100*100的棋盘还有能量，怎么可能跑得了，仔细一想剪枝也无从下手，因为每一步都是必须要走的。

但是，我们从终点开始看，很显然最后一行的元素只能一直向右走。那我们从最后一行m-1个元素看起，从这里出发只有一种走法，再看第m-2个元素，如果能量大于1，则可以一步走到终点，也可以先走到m-1，那走法就加上dp[n-1][m-1]。

由此一来，状态转移方程就容易得出。使用dfs从最后一行枚举每个点进行dfs，看它能到达哪些点，每到一个点就加上那个点在dp数组中的值，一步一步向前搜索。



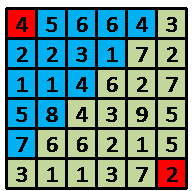
蓝色块是起点能到达的格子，走法就是每个格子的dp数和嘛！

代码如下

#include <bits/stdc++.h>
using namespace std;
int n,m,a[209][209],dp[209][209];
int dfs(int power,int x,int y,int k)
{
	int sumn=k;
	if(dp[x][y]!=0)
		return dp[x][y];
	for(int i=0;i<=power;i++)
	{
		if(x+i>=n)//防止越界
			break;
		for(int j=0;j<=power-i;j++)
		{
			if(y+j>=m)//防止越界
				break;
			if(i==0&&j==0)//不能待在原地不懂
				continue;
			sumn+=dfs(a[x+i][y+j],x+i,y+j,0);
		}
	}
	return sumn;
}
int main()
{
	int t;
	cin>>t;
	while(t--)
	{
		cin>>n>>m;
		memset(dp,0,sizeof(dp));
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<m;j++)
				cin>>a[i][j];
		}
		dp[n-1][m-1]=1;dp[n-1][m]=dp[n][m-1]=1;。。初始化
		for(int i=n-1;i>=0;i--)
			for(int j=m-1;j>=0;j--)
				dp[i][j]=dfs(a[i][j],i,j,0)%10000;//dfs就是求当前格子的走法
		cout<<dp[0][0]<<endl;
	}
}