the least-squares criterion|Sxx|Sxy|Syy|Regression Equation|Outliers|Influential Observations|curvilinear regression|linear regression

4.2 The Regression Equation

Because we could draw many different lines through the cluster of data points, we need a method to choose the “best” line. The method, called the least-squares criterion, is based on an analysis of the errors made in using a line to fifit the data points.

存在有限个可能的的模型（可以使用之后的方法得到模型），从中取出最有可能的2个：并用最小二乘法计算error：

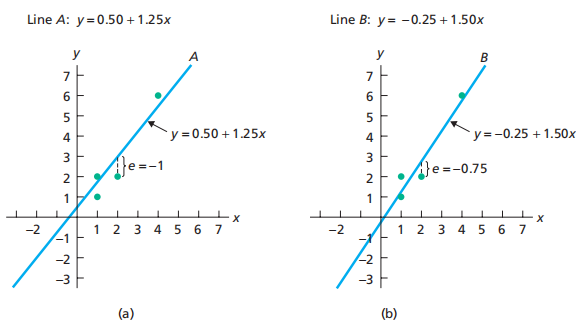
比如（a）中的e

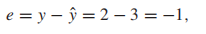
最后得到：

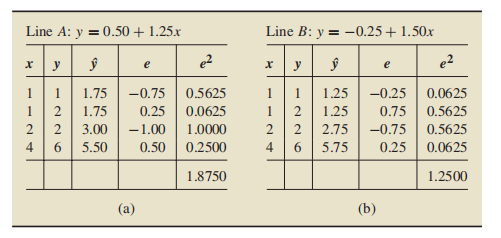
计算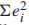，最后确定模型为b，这只是对模型的评价，生成模型可以使用以下方法：

推导：

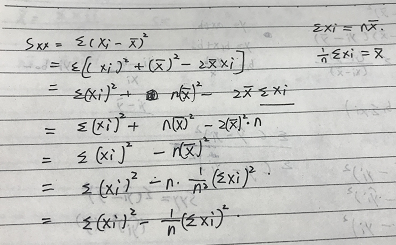
Suppose that a scatterplot indicates a linear relationship between two variables. Then,within the range of the observed values of the predictor variable, we can reasonably use the regression equation to make predictions for the response variable. However,to do so outside that range, which is called extrapolation,

比如减价趋势下的产品价格，离开观测值范围后，价格可能会处于负值状态，所以线性关系必须注明自变量range

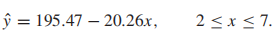
In the context of regression, an outlier is a data point that lies far from the regression line

Outliers and Influential Observations

Outliers是偏离直线太远的值

influential observation ： a data point whose removal causes the regression equation (and line) to change considerably

Eg.在加入（2，169）前后的直线发生了巨大变化，所以（2,169）是一个influential observation

解决办法：

1.缩小x的range

2.添加influential observation 周围的点

Nonetheless, we may need either to remove it—thus limiting the analysis to Orions between 4 and 7 years old—or to obtain additional data on 2- and 3-year-old Orions so that the regression analysis is not so dependent on one data point

outlier和influential observation实际上很难分清：An outlier may or may not be an inflfluential observation, and an inflfluential observation may or may not be an outlier. Many statistical software packages identify potential outliers and inflfluential observations.

否则会出现：

该分布实际上应该为curvilinear regression

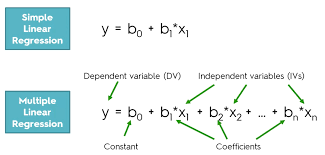
多重线性回归：

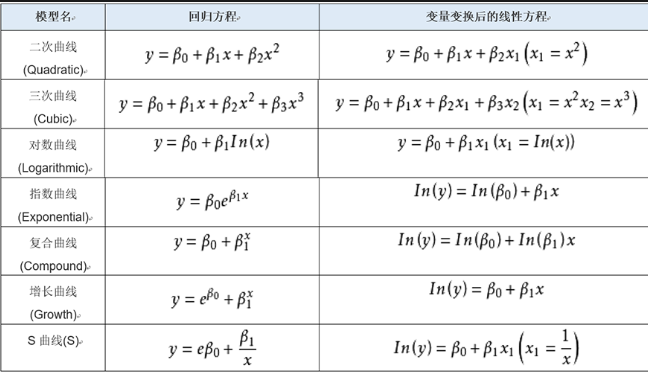
曲线回归：